| 1. |
Examenopgave HAVO wiskunde B, 2009
|
| |
De functie f is gegeven
door f(x) = ln(x + e).
De grafiek van f snijdt de x-as in punt P en de y-as
in punt Q. Zie de figuur hiernaast.
De lijn
y = ax + b gaat door de punten P en Q |
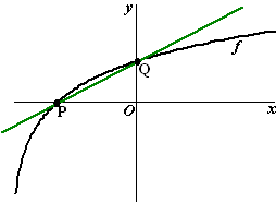 |
| |
|
|
| |
a. |
Bereken de
waarden van a en b exact |
| |
|
|
| |
Punt R
ligt op de grafiek van f.
De helling in punt R is gelijk aan
2/e |
| |
|
|
| |
b. |
Bereken de
x-coördinaat van punt R exact |
| |
|
|
|
| |
|
| 2. |
Gegeven is
de functie f(x) = 3ln(2x) |
| |
|
|
|
| |
a. |
De grafiek
van f is uit de grafiek van y = 3lnx te verkrijgen
door die over een afstand omhoog te schuiven. Welke afstand? |
| |
|
|
|
| |
b. |
De formule
voor f(x) is ook te schrijven als f(x) =
ln(axn).
Voor welke a en b is dat zo? |
| |
|
|
|
| |
c. |
Geef een
vergelijking van de raaklijn aan de grafiek van f in het snijpunt
met de x-as. |
| |
|
|
|
| |
|
|
|
| 3. |
Examenopgave VWO
Wiskunde A, 2003
Vliegtuigen veroorzaken in de buurt van vliegvelden veel
geluidsoverlast. In milieuwetten is vastgelegd welke geluidsbelasting
(hoeveel geluid) nog toegestaan is.
De geluidsbelasting B op een plaats in de buurt van een vliegveld
hangt af van het aantal vliegtuigen dat per jaar passeert en van het
geluidsniveau van elk vliegtuig. Het geluidsniveau per vliegtuig geven we aan met L. Het aantal vliegtuigen per jaar noemen we N.
De formule die het
verband tussen L, N en B geeft is:
B = 20 • log N
+ 4/3L
- 157Voor L, het geluidsniveau per vliegtuig, geldt op zeker
moment L = 72.
Vanzelfsprekend zal een toename van het aantal vliegtuigen ook de
geluidsbelasting doen toenemen. Met behulp van de afgeleide dB/dN
kun je onderzoeken in welke mate dat het geval is. Men wil weten bij welke
waarde van N een toename van 10 000 vliegtuigen de geluidsbelasting
met 1 zal doen toenemen.
Stel een formule op voor dB/dN
en gebruik dB/dN om deze
waarde van N te berekenen. |
| |
|
|
|
| 4. |
Examenopgave VWO
Wiskunde A, 2018 |
| |
In 1992 publiceerden de Amerikaanse wiskundigen Bayer en Diaconis een artikel over
het schudden van kaarten.
Voor dit artikel hadden zij de meest gebruikte manier van schudden
onderzocht, de zogeheten
Riffle
Shuffle (zie de foto).
Zij kwamen tot de conclusie dat het met deze
schudtechniek niet mogelijk is een stapel kaarten écht willekeurig
te maken, zoals bijvoorbeeld een computer dat wel kan.
Voor het spelen van een kaartspel is het goed genoeg als de kaarten
“voldoende willekeurig” geschud zijn. |
 |
| |
Bayer en Diaconis ontdekten tijdens hun
onderzoek dat het aantal keren dat een stapel kaarten minstens
geschud moet worden om als “voldoende willekeurig” bestempeld te
worden, kan worden benaderd met de formule: |
| |
|
|
|
| |
A = 1,5 • 2log(n) |
| |
|
|
|
| |
In deze formule is
A
het aantal keren dat een stapel van
n
kaarten minstens geschud moet worden om als
“voldoende willekeurig” bestempeld te worden.
A
wordt naar boven afgerond op een geheel getal.
Het kaartspel
jokeren wordt gespeeld met twee sets
van 52 speelkaarten, aangevuld met in totaal 4 zogeheten
jokers. |
| |
|
|
|
| |
a. |
Bereken hoe vaak de kaarten bij jokeren minstens
geschud moeten worden volgens de formule van Bayer en Diaconis. |
| |
|
|
|
| |
Als het aantal te schudden kaarten toeneemt, neemt
ook het aantal keren dat er minstens geschud moet worden toe. Dit
aantal neemt echter steeds langzamer toe. Je kunt dit zien aan de
afgeleide dA/dn |
| |
|
|
|
| |
b. |
Stel de formule op van de afgeleide dA/dn
en beredeneer aan de hand van deze formule, dus zonder getallen
in te vullen of een schets te maken, dat
A
afnemend stijgend is. |
| |
|
|
|
| |
In de meeste casino’s kun je het spel
blackjack
spelen. Dat wordt over het algemeen gespeeld
met vier spellen kaarten (totaal 208 kaarten).
Het aantal keer dat zo’n groot aantal kaarten minstens geschud moet
worden is helemaal niet zo groot: volgens de formule van Bayer en
Diaconis slechts 12 keer. Dat is maar drie keer schudden meer dan
bij één spel kaarten.
Volgens de formule van Bayer en Diaconis geldt in
het algemeen: als het aantal kaarten vier keer zo groot wordt, hoeft
er maar drie keer extra geschud te worden. |
| |
|
|
|
| |
c. |
Toon dit aan met behulp van de formule voor
A
en de rekenregels voor logaritmen zonder
gebruik te maken van getallenvoorbeelden. |
| |
|
|
|
| 5. |
Examenopgave VWO
Wiskunde B, 2018-II
Voor a >
0 wordt de functie
fa
gegeven door
fa
(x) =
x -
xln(ax) . |
| |
|
|
|
| |
a. |
Bewijs dat voor elke toegestane
waarde van x geldt: 1/2
• (fa(x) + f1/a(x))
= f1(x) |
| |
|
|
|
| |
Voor elke positieve waarde van a geldt: |
| |
- |
de grafiek van
fa
snijdt de x-as in precies
één punt S (met x-coördinaat
xS); |
| |
- |
de grafiek van
fa
heeft één top T (met x-coördinaat
xT). |
| |
|
|
|
| |
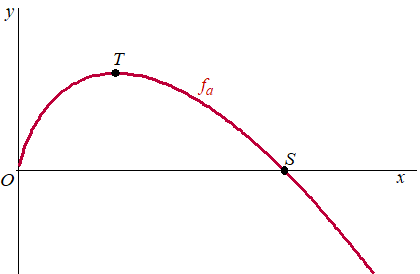
In de figuur zijn voor een waarde van a
de grafiek van fa
en de punten S en
T weergegeven. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Bewijs dat voor elke positieve
waarde van a de verhouding xS/xT
constant is. |
| |
|
|
|
| 6. |
Examenopgave VWO
Wiskunde B, 2019-I |
| |
|
|
|
| |
De functies
f
en
g
worden gegeven door:
f
(x)
=
x
ln(x)
-
x
+
1
en
g(x)
=
f '(x) |
| |
Bereken exact de
x-coördinaten
van de snijpunten van de grafieken van
f
en
g. |
| |
|
|
|
| 7. |
Examenopgave VWO
Wiskunde B, 2022-I |
| |
|
|
|
| |
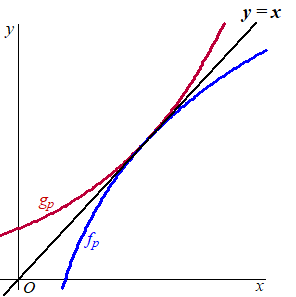
De functies fp
en gp zijn gegeven door: |
 |
| |
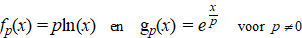 |
| |
|
|
| |
Er bestaat een
waarde van p waarbij de lijn y = x de
gemeenschappelijke raaklijn is van de grafieken van fp
en gp .
Deze situatie is in de figuur hiernaast weergegeven.
Bereken exact de waarde van
p waarvoor de lijn
y = x de gemeenschappelijke
raaklijn is van de grafieken van fp en gp
. |
| |
|
|
|
| |
|
|
|
| |
|
|
 |
| |
|
|
|