| |
©
h.hofstede (h.hofstede@hogeland.nl) |
| 1. |
examenvraagstuk Wiskunde B,
1986.
Met domein R+
is gegeven de functie: f : x
→ 16lnx + x2
- 12x + 11
Ten opzichte van een rechthoekig assenstelsel Oxy is Kf
de grafiek van f. |
| |
|
|
|
| |
a. |
Bewijs dat het punt (1,0) op Kf
ligt.
Bereken in één decimaal nauwkeurig het maximum en het minimum van f. |
| |
|
|
|
| |
b. |
Bewijs dat Kf
precies één buigpunt heeft. |
| |
|
|
|
| 2. |
examenvraagstuk
VWO Wiskunde B,
1986. Met domein R+
is voor elke p ∈ R gegeven de
functie fp : x
→ ln2x
+ 2plnx - 3
Onderzoek welke
waarden het minimum van fp kan aannemen. |
| |
|
|
|
| 3. |
examenvraagstuk
VWO Wiskunde B,
2001. |
| |
|
|
|
| |
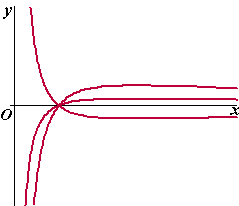
Voor elke a
∈ R\{0} is de functie fa
gegeven door: |
 |
| |
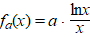 |
| |
In de figuur hiernaast is de
grafiek van fa getekend voor enkele waarden van
a. |
| |
|
|
| |
a. |
Bereken voor welke waarde
van a de maximale y-coördinaat van een punt op de
grafiek van fa gelijk is aan 3. |
| |
|
|
|
| |
b. |
Bereken de waarden van a
waarvoor de grafiek van fa de x-as snijdt
onder een hoek van 30º |
| |
|
|
|
| 4. |
examenvraagstuk
VWO Wiskunde B,
2001. |
| |
|
|
|
| |
De functies f en g
zijn gegeven door:
f(x) = ln2x
g(x) = ln(2 - x)
Hiernaast zijn de grafieken van f en g getekend met
snijpunt S |
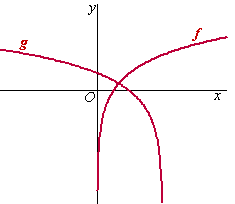 |
| |
|
|
| |
a. |
Bereken de hoek waaronder de
grafieken van f en g elkaar snijden; geef het antwoord in
graden nauwkeurig. |
| |
|
|
|
| |
De lijn met vergelijking x
= p snijdt de grafiek van f in het punt A en de grafiek
van g in het punt B. |
| |
|
|
|
| |
b. |
Bereken p in het geval
dat AB = ln2. |
|
| |
|
|
|
| |
C is het punt van de grafiek van
f waarvoor geldt dat de richtingscoëfficiënt van de lijn OC
maximaal is. |
| |
|
|
|
| |
c. |
Bereken de coördinaten van C. |
| |
|
|
|
| 5. |
examenvraagstuk
HAVO Wiskunde B,
2003. Gegeven is de functie f
(x) = 2 ln(x + 1) + ln (2 - 2x) |
| |
|
|
|
| |
a. |
Bereken het domein van f . |
| |
|
|
|
| |
b. |
Bereken met behulp van
differentiëren de exacte waarde van de x-coördinaat van de
top van de grafiek van f. |
| |
|
|
|
| |
|
| 6. |
examenvraagstuk
HAVO Wiskunde B,
2004. Gegeven is de functie f(x)
= ln(4 - x).
Gegeven is verder de functie g(x)
= 2 • ln(x + 2)
Met domein -2 < x
< 4 is de functie h gegeven door h(x) = f(x)
+ g(x)
Het functievoorschrift van h kan geschreven worden
als h(x) = ln(16 + 12x - x3) |
| |
|
|
.gif) |
| |
a. |
Toon dit algebraïsch aan. |
| |
|
|
| |
Op de grafiek van h
ligt een punt B.
In dit punt B is de richtingscoëfficiënt van de raaklijn aan de
grafiek van h gelijk aan 2.
Zie de figuur hiernaast. |
| |
|
|
| |
b. |
Bereken met behulp van differentiëren van
h de x-coördinaat van B.
Rond je antwoord af op twee decimalen. |
| |
|
|
|
| |
|
|
|
| 7. |
examenvraagstuk Wiskunde B,
1986. Een gezonde volwassene is ’s morgens
langer dan aan het einde van de dag. De Australische wetenschapper D.
Burgess heeft dit verschijnsel onderzocht en publiceerde in 1999 de
volgende formule voor de lengtefractie S:
S = ln(−0,00216t + 2,7183) . Hierin is t het aantal uren
nadat een persoon is opgestaan en S de verhouding tussen de lengte L van
die persoon ten opzichte van zijn lengte L0 bij het opstaan.
Dus S = L/L0
Meneer Jansen heeft als hij uit bed komt een lengte van 170,0 cm. |
| |
|
|
|
| |
a. |
Bereken na hoeveel tijd
meneer Jansen volgens de formule 2,0 cm korter is geworden. Geef je
antwoord in minuten nauwkeurig. |
| |
|
|
|
| |
We gaan er in het vervolg
van de opgave van uit dat een persoon na het opstaan 16 uur actief is,
dus na 16 uur weer gaat slapen. |
| |
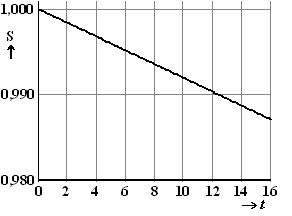
In de figuur hiernaast is de
grafiek van S als functie van t getekend. Deze grafiek lijkt zo
op het eerste gezicht een rechte lijn, maar door de formule weten wij
dat dit niet zo is. |
 |
| |
|
|
| |
b. |
Leg met behulp van de tweede afgeleide
uit of er voor
0 ≤ t ≤ 16 sprake is van toenemende of afnemende
daling |
| |
|
|
| |
De grafiek van S valt
nagenoeg samen met de rechte lijn door de punten (0; 1,0000) en (16;
0,9872). |
| |
Is de formule van S met de
natuurlijke logaritme, zoals gepubliceerd door de Australische
wetenschapper, niet onnodig ingewikkeld? We zouden voor S ook gewoon een
lineaire functie van t kunnen
nemen.
We vergelijken daarom de formule S = ln(−0,00216t + 2,7183) met
de formule S = −0,0008t +1,0000 die hoort bij de rechte lijn door
de punten (0; 1,0000) en (16; 0,9872). We nemen weer meneer Jansen, met
een lengte van 170,0 cm bij het opstaan, als voorbeeld. Met behulp van
beide formules kun je op elk tijdstip t (met 0 ≤ t ≤16 )
de lengte van meneer Jansen in de loop van de dag uitrekenen. Ook kun je
op elk tijdstip t het verschil tussen de uitkomsten van beide
formules bekijken. |
| |
|
|
|
| |
c. |
Bereken het maximale
verschil voor de lengte van meneer Jansen dat de twee formules kunnen
opleveren. |
| |
|
|
|
| |
|
|
|
| 8. |
examenvraagstuk
VWO, Wiskunde B,
2010. |
|
| |
|
|
 |
| |
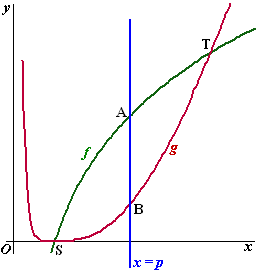
De functies f en g zijn gegeven door f(x)
= 4 • lnx en g(x) = (lnx)4
met x > 0 . De grafieken van f en g snijden elkaar
in de punten S en T.
Een lijn x = p snijdt tussen S en T de grafiek van f
in A en de grafiek van g in B. Zie de figuur.
Er is een waarde van p waarvoor de lengte van
lijnstuk AB maximaal is.
Bereken exact de maximale lengte van AB.
Schrijf je antwoord zo eenvoudig mogelijk. |
| |
|
|
| |
|
|
| |
|
|
|
| 9. |
Examenvraagstuk
VWO Wiskunde B, 2009 |
|
| |
|
|
|
| |
De functies f en g zijn gegeven
door f(x) = ln(x) en g(x) = ex
. In onderstaande figuur zijn de grafieken van beide functies getekend. De
lijn k is een gemeenschappelijke raaklijn aan de grafieken van f
en g. Het punt waarin k de grafiek van f raakt,
noemen we P( p, ln(p)) , met p > 0. Het punt waarin
k de grafiek van g raakt, noemen we Q(q, eq
), met q < 0 . Omdat k raaklijn is in
punt P aan de grafiek van f,
is y =
1/p x
+ ln(p) − 1 een formule voor k. |
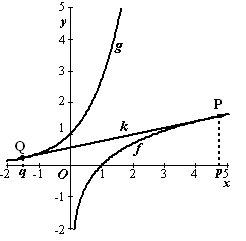 |
| |
|
|
| |
a. |
Toon dit aan. |
| |
|
|
| |
|
| |
Omdat k raaklijn is in
punt Q aan de grafiek van g, is ook y = eq x
+ eq(1 − q) een formule voor k. |
| |
|
|
|
| |
Uit de twee formules voor k kunnen we twee verbanden tussen p en
q afleiden: eq = 1/p
(oftewel p = e−q )
en eq(1
− q) = ln(p) −1.
Uit deze twee verbanden volgt dat q voldoet aan de vergelijking:
eq = (q + 1)/(q - 1) |
| |
|
|
|
| |
b. |
Toon aan dat deze laatste vergelijking volgt
uit de twee genoemde verbanden tussen p en q. |
| |
|
|
|
| |
c. |
Bereken in twee decimalen nauwkeurig de
richtingscoëfficiënt van de gemeenschappelijke raaklijn k. |
| |
|
|
|
| 10. |
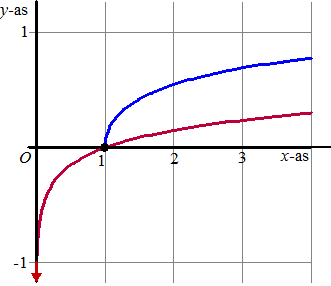
Hiernaast zie je de
grafieken van
f(x) = ln(√x)
en g(x) = √(lnx)
Het lijkt erop dat de grafieken elkaar snijden in (1, 0). Dat is ook zo.
Er is nog een snijpunt van beide grafieken. |
 |
| |
|
|
| |
a. |
Geef de coördinaten van dat
tweede snijpunt. |
| |
|
| |
Twee evenwijdige
lijnen raken de grafieken van f en g voor dezelfde x
= p |
| |
|
|
| |
b. |
Bereken de verticale afstand
tussen deze lijnen. |
| |
|
|
|
| |
|
|
|
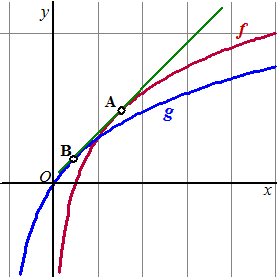
| 11. |
Hiernaast zie je de grafieken van
f(x) = ln(2x) en g(x) = ln(x
+ 1)
Een rechte lijn raakt beide grafieken; de grafiek van f in
punt A en de grafiek van g in punt B. Zie de figuur.
In dat geval geldt xA - xB = 1 |
 |
| |
|
|
| |
a. |
Toon dat aan. |
| |
|
|
| |
b. |
Bereken de x-coördinaat van A. |
| |
|
|
|
| |
|
|
|
| 12. |
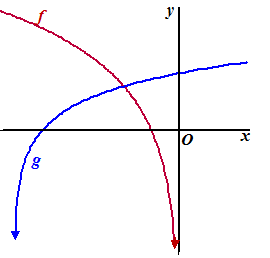
Gegeven zijn de
functies :
f(x) = 2ln(-x) en g(x) = ln(x
+ 6) |
 |
| |
|
|
| |
a. |
Los algebraïsch op:
g(x) ≤ f(x)
|
| |
|
|
| |
De lijn
x = p snijdt de grafieken van f en g in de
punten A en B. De raaklijnen in A en B aan de grafieken f en
g vormen
samen met AB een gelijkbenige driehoek met basis AB. |
| |
|
|
| |
b. |
Bereken algebraïsch de waarde van
p. |
| |
|
|
| |
c. |
Bereken de oppervlakte van deze
driehoek. |
| |
|
|
|
| 13. |
Examenvraagstuk
VWO Wiskunde B, 2017-I |
| |
|
|
|
| |
De functies f en
g zijn gegeven door: f(x) = lnx
en g(x) = (1/2e)
• x2
Ga na met exacte berekening of
de grafieken van f en g elkaar raken. |
| |
|
|
|
| 14. |
Examenvraagstuk
VWO Wiskunde A, 2018-I De Shannon-index
H
is een maat voor de diversiteit
(verscheidenheid) van een dieren- of plantenpopulatie in een gebied.
Hoe hoger de Shannon-index, hoe groter de diversiteit.
We kijken naar een gebied met twee soorten bomen. De formule voor de
Shannon-index is dan:
H = -
(
p1
ln(
p1)
+
p2
ln(
p2
))
waarin
p1
en
p2
de aandelen van elke soort binnen het
gebied zijn. Er geldt bijvoorbeeld dat
p1
=
0,37
als 37% van de bomen uit soort 1 bestaat.
Bos A bestaat voor 70% uit eiken en voor 30% uit
beuken en bos B bestaat voor 90% uit eiken en voor 10% uit beuken. |
| |
|
|
|
| |
a. |
Onderzoek met de formule voor
H
van welk van beide bossen de Shannon-index het
grootst is. |
| |
|
|
|
| |
In een bos met twee soorten bomen, eiken en beuken,
geldt: als
p het aandeel eiken is, is het
aandeel beuken gelijk
aan 1 –
p.
De formule voor de Shannon-index kan dan geschreven worden als:
H =
- (pln(
p)
+
(1
-
p)ln(1
-
p)) |
| |
|
|
|
| |
b. |
Onderzoek met de grafische rekenmachine tot welke
waarde de Shannonindex nadert als het aandeel eiken in het bos
steeds kleiner wordt. |
| |
|
|
|
| |
c. |
Bereken met behulp van dH/dp
voor welke percentages eiken en beuken de Shannon-index
H
van het bos maximaal is |
| |
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |