© h.hofstede (h.hofstede@hogeland.nl)

       
1. a. f(1) = 16ln1 + 12 - 12 + 11 = 0

f '(x) = 16/x + 2x - 12 = 0
16 + 2x2 -12x = 0
x2 - 6x + 8 = 0
(x - 4)(x - 2) = 0
x = 4  ∨  x = 2

f(4) = 16ln4 + 42 - 12 • 4 + 11 = 16ln4 - 21
f(2) = 16ln2 + 22 - 12 • 2 + 11 = 16ln2 - 9

Het maximum is  (2, 16ln2 - 9) en het minimum is (4, 16ln4 - 21)

 
       
  b. f '' = -16x-2 + 2 = -16/x2 + 2
f '' = 0  geeft  16/x2 = 2
x2 = 8
x = √8  ∨   ( x = -√8 maar die kan niet want dan bestaat lnx niet)
Dus er is één buigpunt, namelijk bij  x = √8		  
       
2. f(x) =  ln2x + 2plnx - 3
f '(x) =  2lnx • 1/x + 2p • 1/x = 2/x • (lnx + p)
f '(x) = 0  ⇒   lnx = -p  ⇒   x = e-p
Het minimum is dan y = ln2(e-p) + 2pln(e-p) - 3  = p2 - 2p - 3
Dat is een dalparabool met de top bij  p = 1
Dan is het minimum  y = -4
Het minimum kan alle waarden  groter of gelijk aan -4 aannemen.  
       
3. a.  
    f ' = 0  geeft  1 - lnx = 0 Þ  x = e
het maximum is f(e) = a• lne/e = a • 1/e
a • 1/e = 3  
a = 3e		  
       
  b. Als de grafiek de x-as onder een hoek van 30º snijdt is de helling gelijk aan tan30º = 1/3√3
De grafiek snijdt de x-as bij y = 0  dus als lnx = 0  dus  x = 1
Dus moet gelden  f '(1) =  1/3√3
a • (1 - ln1)/12 =  1/3√3
a = 1/3√3

De hoek is ook 30º als de helling gelijk is aan -1/3√3 en dat geeft op dezelfde manier a = -1/3√3
       
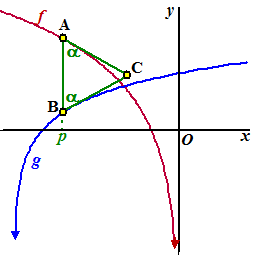
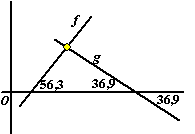
4. a. ln2x = ln(2 - x)
2x = 2 - x
3x = 2
x = 2/3

f '(x) = 1/(2x) • 2 = 1/x  dus  f '(2/3) = 3/2
de raaklijn aan de grafiek van f maakt een hoek met de x-as waarvoor geldt  tanα = 3/2  ⇒  α = 56,3º

g '(x) = 1/(2 - x) • -1   dus  g '(2/3) = -3/4
de raaklijn aan de grafiek van f maakt een hoek met de x-as waarvoor geldt  tanα = -3/4  ⇒  α = -36,9º
       
    de hoek tussen de grafieken is dan  180 - 56,3 - 36,9 = 86,6º
zie de schets hiernaast
Dat is dus ongeveer 87º
       
  b. f(p) = ln2p  en  g(p) = ln(2 - p)
Er zijn twee mogelijkheden waarbij het lijnstuk AB gelijk is aan ln2.

ln2p - ln(2 - p) = ln2
ln(2p/(2 - p)) = ln2
2p/(2-p) = 2
2p = 2(2 - p)
2p = 4 - 2p
4p = 4
p = 1

ln(2 - p) - ln2p = ln2
ln((2 - p)/2p) = ln2
(2 - p)/(2p) = 2
2 - p = 4p
2 = 5p
p = 21/2
       
  c. C is het punt  (x, ln2x)
De helling van OC is dan  Δy/Δx = ln2x/x  en die is maximaal als de afgeleide ervan nul is.
     
    Dat is nul als  1 - ln(2x) = 0
ln(2x) = 1
2x = e
x = 1/2e
Dan is  y = 1, dus dat is het punt  (1/2e, 1)		  
       
5. a. Het domein van ln x is  x > 0
dus moet gelden x + 1 > 0  en  2 - 2x > 0
dat geeft  x > -1  en  x < 1  dus het domein is  〈-1,1〉
       
  b.
    (de factoren 1 en -2 komen van de kettingregel)
f '(x) = 0 
⇒  2/(x + 1) = 2/(2 - 2x) 
⇒ (kruislings vermenigvuldigen) ⇒  2(x + 1) = 2(2 - 2x)
⇒  2x + 2 = 4 - 4x 
⇒  6x = 2 
⇒  x = 1/3  
       
6. a. ln(4 - x) + 2 • ln(x + 2)
= ln(4 - x) + ln(x + 2)2
= ln{(4 - x)•(x + 2)2}
= ln{(4 - x)•(x2 + 4x + 4)}
= ln{4x2 + 16x + 16 - x3 + 4x2 - 4x}
= ln(16 + 12x - x3)
       
  b.  
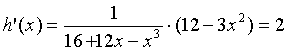    ⇒  2•(16 + 12x - x3) = 12 - 3x2
Dat lukt niet algebraïsch (derdegraads vergelijking), daarom maar met de GR.
Y1 = 2•(16 + 12x - x3)  en Y2 = 12 - 3x2  en dan intersect levert  x = -1,09 
(x = 4,589.. is geen oplossing want die bevindt zich niet binnen het domein)
       
7. a. 168/170 =  ln(−0,00216 • t + 2,7183)
0,9882 =  ln(−0,00216 • t + 2,7183)
e0,9882 = −0,00216 • t + 2,7183
2,6864 = −0,00216 • t + 2,7183
-0,0318 = -0,00216 • t
t = 14,727 uur en dat is 14 uur en 44 minuten		  
       
  b. S = ln(−0,00216t + 2,7183)
S ' =  -0,00216 • 1/(-0,00216t + 2,7183) = -0,00216 • (-0,00216t + 2,7183)-1
S'' = 0,00216 • (-0,00216t + 2,7183)-2 • -0,00216 = -0,00000467 • (-0,00216t + 2,7183)-2 
Dat deel tussen haakjes is een kwadraat dus altijd positief.
door dat negatieve getal -0,00000467 is S''  dus altijd negatief.
dat betekent dat S' negatief is en dalend, dus S zelf is toenemend dalend.
       
  c. het verschil is  ln(−0,00216t + 2,7183) - (−0,0008t +1,0000)
voert deze formule in bij Y1 in de GR en gebruik calc = maximum
dat geeft een maximum van S = 0,00002955  (bij x = 8,47)
dan is het verschil in lengte  0,00002955 • 170 = 0,005 cm.
       
8. De lengte L  van AB is  L = f(p) - g(p)
L = 4lnp - (lnp)4
Dat is maximaal als de afgeleide nul is.
L' = 4 • 1/p  - 4(lnp)3 • 1/p = 0     (kettingregel)
1/p • (4 - 4lnp)3 = 0
4 - 4(lnp)3 = 0
(lnp)3 = 1
lnp = 1
p = e
Dan is  L = 4lne - (lne)4 = 4 - 1 = 3
       
9. a. f '(x) = 1/x  dus  f '(p) = 1/p en dat is de richtingscoëfficiënt van de raaklijn.
De raaklijn heeft dus vergelijking  y = 1/p • x + b  en moet door  (p, lnp) gaan
Invullen geeft  lnp = 1/p • p + b  dus  b = lnp - 1
Daarmee wordt de vergelijking  y = 1/p • x + lnp - 1
       
  b. Als e -q  = p  dan is  ln p = -q
Dat geeft in de tweede vergelijking eq (1 - q) = -q - 1
Daaruit volgt;
       
  c. Voer in de GR in:
Y1 = e ^ X
Y2 = (X + 1) / (X - 1)
intersect  levert X = q ≈ -1,543
Dus de richtingscoëfficiënt is ongeveer  eq = e-1,543 ≈ 0,21
       
10. a. ln(√x) = √(lnx)
ln2(√x) = lnx
ln2(√x) = ln(√x)2
ln2(√x) = 2ln(√x)
ln2(√x) - 2ln(√x) = 0
ln(√x) • (ln(√x) - 2) = 0
ln(√x) = 0  ∨  ln(√x) = 2
√x = 1  ∨   √x =  e2
x = 1 ∨  x = e4
Het tweede snijpunt is  (e4, 2) 
       
  b. f(x) = ln(√x)
f '(x) = 1/√x • 1/2√x  = 1/(2x)

g(x) = √(lnx)
g '(x) =  1/2√(lnx) • 1/x  = 1/(2x√(lnx))

f ' =  g'   ⇒   1/2x = 1/(2x√(lnx))   ⇒  √(lnx) = 1  ⇒  lnx = 1  ⇒  x = e

f(e) =  1/2  en  g(e) = 1  dus de afstand is  1/2.
       
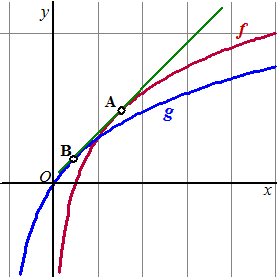
11. a. De hellingen in A en B zijn gelijk

f ' = 1/2x • 2 = 1/x  dus  f '(xA) = 1/xA
g' = 1/(x + 1)  dus  g'(xB) = 1/(xB + 1)

1/xA = 1/(xB + 1)
xA = xB + 1
xA - xB = 1
     
  b. noem xA = p  dan is  xB = p - 1
yA = ln(2p)  en  yB = ln(1 + p - 1) = ln(p)
De lijn AB heeft dus helling   Δy/Δx = ln(2p) - ln(p)  (want Δx = 1)
Dat moet gelijk zijn aan de hellingen in A en B aan de grafiek
ln(2p) - ln(p) = 1/p
ln(2p/p) = ln2 = 1/p
e2 = 1/p
p = 1/e²  en dat is  xA
       
12. a. 2ln(-x) = ln(x + 6)
ln(-x)2 = ln(x + 6)
(-x)2 = x + 6
x2 - x - 6 = 0
(x - 3)(x + 2) = 0
x = 3 ∨  x = -2
Het snijpunt is x = -2

Het domein van g is  〈-6, →〉 dus de ongelijkheid geldt voor   -6 < x ≤ -2
       
  b. Als de driehoek gelijkbenig is met basis AB zijn de hellingen van AC en BC tegengesteld.
f '(p) = -g'(p)
2 • 1/-p • -1 =  - 1/(p + 6)
2/p =  - 1/(p + 6)
2(p + 6) = -p
3p = -12
p = -4

     
  c. AB = ln4 - ln2 = ln2
f '(-4) = -1/2 = Δy/Δx  dus  de hoogte van de driehoek is
Δx = 2Δy = 2 • 1/2ln2 = ln2
De oppervlakte is dan  1/2 • ln2 • ln2  = 1/2ln22
       
13. Als ze elkaar raken zijn de functies gelijk en de afgeleides ook
f ´(x) = 1/x
g '(x) = 1/2e • 2x = x/e
1/x = x/e  geeft  x2 = e
x = √e   (-√e mag niet want dan bestaat lnx niet)

f(√e)  = ln(√e) = ln(e0,5) = 0,5
g(√e) = 1/2e • (√e)2 = 0,5

Die zijn gelijk dus de grafieken raken elkaar.
       
14. a. HA = -(0,7ln(0,7) + 0,3ln(0,3)) = 0,61
HB = -(0,9ln(0,9) + 0,1ln(0,1)) = 0,33
Dus de Shannon-index van bos A is het grootst.
       
  b. Als het aandeel eiken steeds kleiner wordt gaat p naar nul toe.
p = 0,1 geeft H = 0,33
p = 0,01 geeft  H = 0,056
p = 0,001  geeft  H = 0,0079
p = 0,0001 geeft  H = 0,0010
Dat nadert tot nul.
       
  c. H = - (pln( p) + (1 - p)ln(1 - p))
H ' =  -(1 • lnp + p • 1/p +  -1 • ln(1 - p) + (1 - p) • 1/(1 - p) • -1)
= -(lnp + 1 - ln(1 - p) - 1)
= -lnp + ln(1 - p) 

Voor het maximum moet gelden  H ' = 0
-lnp + ln(1 - p) = 0
lnp = ln(1 - p)
p = 1- p
2p = 1
p = 0,5
Dus 50% eiken en 50% beuken.
       

© h.hofstede (h.hofstede@hogeland.nl)