| 1. |
De
oppervlakte tussen de grafiek van y = 3sin0,5x en de
x-as voor x tussen 0 en p blijkt gelijk te zijn aan
15.
Bereken p algebraïsch. |
| |
|
|
|
| |
|
|
|
| 2. |
examenvraagstuk VWO Wiskunde
B, 1998. |
| |
|
|
|
| |
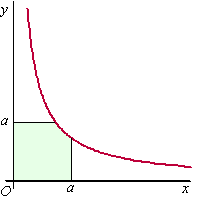
Gegeven is de functie f :
x → 2/x
met domein R+. Voor a >
√2 is Va het
vlakdeel begrensd door de x-as, de lijn x = a,
de lijn y = a en de grafiek van f (zie de
figuur).
Bereken a in het geval dat de
oppervlakte van Va gelijk is aan 6. |
 |
| |
|
|
|
|
| 3. |
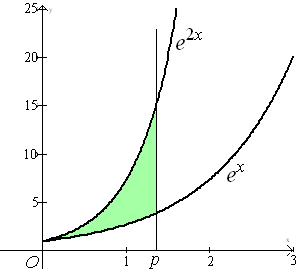
De
oppervlakte, ingesloten door de grafieken van y = ex
en e2x en de lijn x = p
is gelijk aan 8.
Bereken p |
 |
| |
|
|
|
|
| 4. |
examenvraagstuk VWO Wiskunde
B, 2001. |
| |
|
|
|
 |
| |
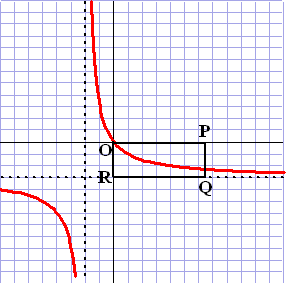
Gegeven is de functie:
f(x) = 6/(x + 2) -
3
In de figuur hiernaast is rechthoek OPQR
getekend met R(0,-3) en P(b,0) met b > 0
De grafiek van f verdeelt de rechthoek in twee delen met gelijke
oppervlakte.
Bereken b in twee decimalen nauwkeurig. |
| |
|
|
|
| |
|
|
|
|
| 5. |
examenvraagstuk VWO Wiskunde
B, 2005. |
| |
|
|
|
|
| |
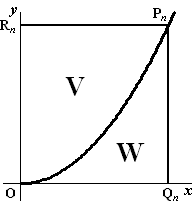
De grafiek van y =
1/nx2
verdeelt het vierkant OQnPnRn
in twee stukken V en W.
Zie de figuur hiernaast.
De verhouding van de oppervlakten van V en W is
onafhankelijk van n Toon dit aan |
 |
| |
|
|
|
|
| 6. |
examenvraagstuk VWO Wiskunde
B, 2007. |
| |
|
|
|
|
| |
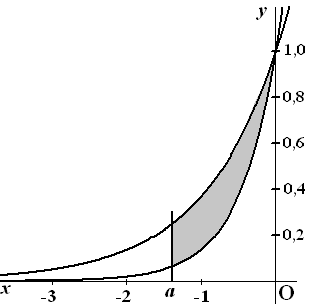
We bekijken de grafieken van de functies
f en g, gegeven
door f(x) = ex
en g(x)
= e2x voor
x ≤ 0. In de volgende figuur staan de
grafieken van deze functies. De schaal op de y-as
is anders gekozen dan de schaal op de x-as. Voor elke a <
0 is de oppervlakte van het vlakdeel dat wordt ingesloten door de grafieken
van f en g en de lijn x = a gelijk
aan
1/2(1
- ea )2
Toon dit op algebraïsche wijze aan. |
 |
| |
|
|
|
|
| 7. |
examenvraagstuk VWO Wiskunde
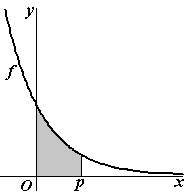
B, 2008. De functie f is
gegeven door f(x) = e−2x.
In de
figuur hiernaast is voor een waarde van p het
vlakdeel grijs gemaakt dat wordt ingesloten
door de grafiek van f, de lijn x =
p, de x-as en de y-as.
Toon aan
dat de oppervlakte van dit vlakdeel voor elke positieve waarde van p
kleiner is dan 1/2 . |
 |
| |
|
|
|
|
| 8. |
examenvraagstuk VWO Wiskunde
B, 2010. De parabool met vergelijking
y = 4x − x2 en de x-as sluiten een vlakdeel
V in. De lijn y = ax (met 0 ≤ a < 4 ) snijdt
de parabool in de oorsprong O en in punt A. Zie de figuur hiernaast.
A heeft de coördinaten (4 -
a, 4a
- a2) |
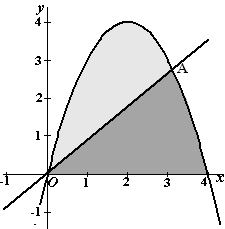 |
| |
|
|
|
| |
a. |
Toon dit aan. |
| |
|
|
|
| |
Het deel van V boven de lijn OA
heeft oppervlakte 1/6(4
- a)3 |
| |
|
|
|
| |
b. |
Toon dit aan. |
| |
|
|
|
|
| |
c. |
Bereken exact voor welke waarde
van a de lijn y = ax het gebied V verdeelt in twee delen
met gelijke oppervlakte. |
| |
|
|
|
|
| |
|
|
|
|
| 9. |
examenvraagstuk VWO Wiskunde
B, 2011. Voor elke positieve waarde van a is
de functie fa gegeven door
fa(x) = sinx + a • sin(2x) op
het domein [0, π].
Voor elke waarde van a
waarvoor geldt 0 < a < 1/2
ligt de grafiek van fa tussen (0, 0) en (π, 0) geheel boven de x-as.
Hiernaast is een
dergelijke grafiek getekend.
Toon aan dat de oppervlakte van het
vlakdeel dat wordt begrensd
door de grafiek van fa en de x-as,
onafhankelijk is van a. |
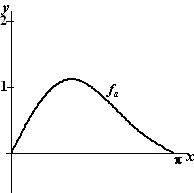 |
| |
|
|
|
|
| 10. |
examenvraagstuk VWO Wiskunde
B, 2012.
Voor elke positieve waarde van
p
is een functie
f
gegeven door: f
(x) = -x3 + 3px2
De grafiek van f
heeft twee punten met de
x-as
gemeenschappelijk: O(0, 0)
en punt
A.
De top van de grafiek van f
die rechts van de
y-as
ligt, noemen we T.
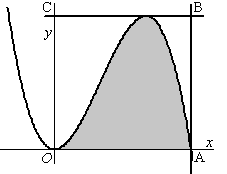
De horizontale lijn door
T
snijdt de
y-as
in punt C
en snijdt de verticale lijn door
A
in punt
B.
De oppervlakte van het gebied onder de grafiek van
f
binnen rechthoek
OABC
is in de figuur grijs gemaakt. |
 |
| |
|
|
|
|
| |
Toon aan dat de verhouding van de oppervlakte van het
grijze gebied en de oppervlakte van rechthoek
OABC
onafhankelijk is van
p. |
| |
|
|
|
|
| 11. |
examenvraagstuk VWO Wiskunde
B, 2014.
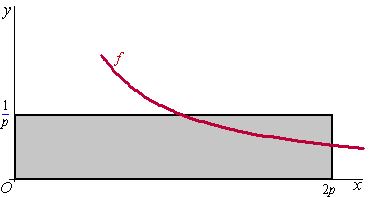
Voor x > 0 is de functie f
gegeven door f(x) = 1/x
In onderstaande figuur is voor p > 0 een rechthoek getekend
die wordt begrensd door de lijnen met vergelijkingen x = 2p
en y = 1/p de x-as
en de y-as. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
Voor elke positieve waarde van p
verdeelt de grafiek van f de rechthoek in twee stukken.
Bewijs met behulp van integreren dat de
oppervlakte van elk van deze stukken onafhankelijk is van de waarde
van p. |
| |
|
|
|
|
| 12. |
examenvraagstuk VWO Wiskunde
B, 2014. |
| |
|
|
|
|
| |
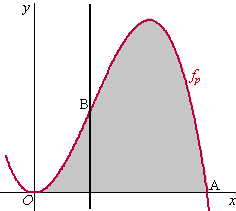
Voor p > 0 is de functie fp
gegeven door fp(x) = 3px2
- x3
De grafiek van fp raakt de x-as in het punt
O(0, 0) en snijdt deze in het punt A(3p, 0) .
Verder heeft de grafiek van fp een buigpunt B(p,
2p3).
V is het gebied dat wordt ingesloten
door de grafiek van fp en de x-as.
De verticale lijn door het buigpunt verdeelt V in twee delen.
In de figuur hiernaast is deze situatie weergegeven. De
oppervlakte van het linkerdeel is 3/4p4.
Bewijs dat de oppervlakte van het
rechterdeel acht keer zo groot is als de oppervlakte van het
linkerdeel. |
 |
| |
|
|
|
|
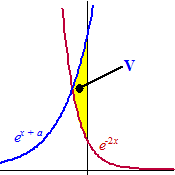
| 13. |
De grafieken van y
= e-2x en y = ex
+ a en de y-as sluiten een vlakdeel V in dat
exact oppervlakte 1/2
heeft.
Bereken algebraïsch voor welke waarde van a dat geldt. |
 |
| |
|
|
|
|
| 14. |
examenvraagstuk
VWO wiskunde B, 2015.
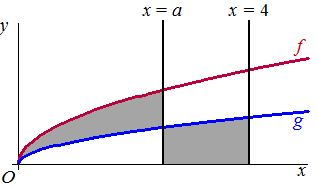
In de figuur zijn
de grafieken getekend van de functies f en g gegeven door
f(x) = √x
en g(x) = 1/2√x.
Verder zijn de lijnen getekend met vergelijkingen x = a
en x = 4 met 0 < a < 4. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
In de figuur zijn
twee vlakdelen grijs gemaakt. Het ene grijze vlakdeel wordt begrensd
door de grafieken van f en g en de lijn met vergelijking
x = a. Het andere grijze vlakdeel wordt begrensd door de
grafiek van g, de x-as en de lijnen met vergelijkingen
x = a en x = 4.
Bereken exact voor
welke waarde van a deze vlakdelen gelijke oppervlakte hebben. |
| |
|
|
|
|
| 15. |
examenvraagstuk
VWO wiskunde B, 2015.
Op het domein [-9,0] is de functie f gegeven door f(x)
= √(x
+ 9) . In de figuur is de grafiek van f getekend en een lijn met
vergelijking x = p met -9 < p
≤ 0. Het gebied dat wordt ingesloten door de
grafiek van f, de x-as en deze lijn is met grijs
aangegeven. |
| |
|
|
|
|
| |
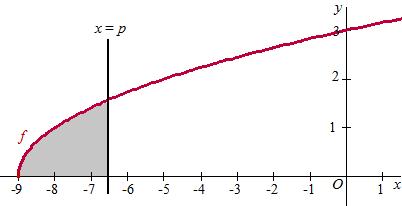 |
| |
|
|
|
|
| |
De oppervlakte van
het grijze gebied noemen we A. De waarde van A hangt af van de waarde
van p.
Er geldt: |
| |
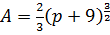 |
| |
|
|
|
|
| |
a. |
Toon deze formule
aan. |
| |
|
|
|
|
| |
b. |
Er is een waarde
van p waarvoor A(p) het achtste deel is van de
oppervlakte van het gebied dat wordt ingesloten door de grafiek van f,
de x-as en de y-as. Bereken exact deze
waarde van p. |
| |
|
|
|
|
| 16. |
P is de parabool y
= x2 |
| |
|
|
|
|
| |
a. |
Het vlakdeel,
ingesloten door P en de lijn y = 3x, wordt gewenteld om de
y-as. Bereken de inhoud van het lichaam dat daardoor ontstaat. |
| |
|
|
|
|
| |
b. |
Q is een punt van de
parabool met xQ = a.
V is het vlakdeel in gesloten door de grafiek van P de lijn OQ en de
lijn x = 2a
V bestaat uit twee delen, waarvan de totale oppervlakte gelijk is
aan 8.
Bereken a |
| |
|
|
|
|
| 17. |
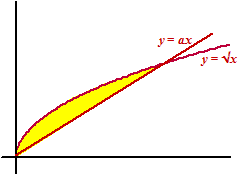
De grafiek van y
= √x en de lijn y = ax
sluiten een vlakdeel V in dat oppervlakte 102/3
heeft.
Bereken a. |
 |
| |
|
|
|
|
| 18. |
Examenvraagstuk
VWO Wiskunde B, 2018-II De functie f is gegeven door f
(x) =
x2.
De raaklijn aan de grafiek van f
in een punt P(p, p2)
met p >
0 snijdt de x-as
in een punt A.
V is het vlakdeel dat wordt
ingesloten door de grafiek van f en de lijn
OP.
Zie de figuur. |
| |
|
|
|
|
| |
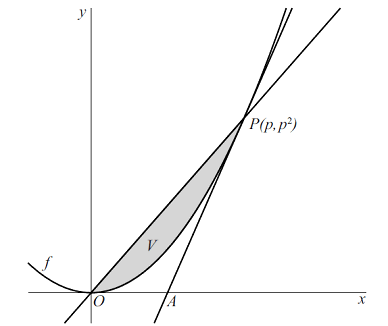 |
| |
|
|
|
|
| |
Bewijs dat de oppervlakte van driehoek
OAP anderhalf keer zo
groot is als de oppervlakte van
V. |
| |
|
|
|
|
| 19. |
Examenvraagstuk
VWO Wiskunde I, 1974-I |
| |
|
|
|
|
| |
Gegeven zijn de
functies f(x) = x2 en
g(x) = (x³ + 2)/x De lijnen x
= k en x = 2k en de grafieken van f en
g sluiten een vlakdeel V in.
Bewijs dat de oppervlakte van V voor k > 0
onafhankelijk is van k.
Onderzoek of deze onafhankelijkheid ook geldt voor k < 0. |
| |
|
|
|
|
| 20. |
Examenvraagstuk
VWO Wiskunde B, 2022-II |
| |
|
|
|
|
| |
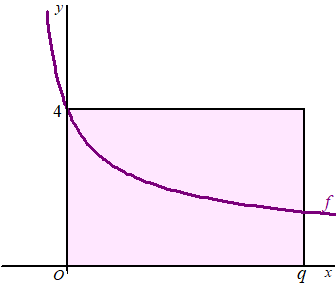
De functie f is
gegeven door: f(x)
= 4/√(x + 1)
De grafiek van f snijdt de y-as in
het punt (0, 4). In de figuur hiernaast is de
grafiek van f weergegeven. Ook is de
rechthoek weergegeven die wordt begrensd door de x-as, de
y-as, de lijn met vergelijking y = 4 en de lijn
met vergelijking x = q met q >
0 . De grafiek van f verdeelt deze rechthoek in twee
delen.
Er is één waarde van q waarbij de oppervlaktes van deze
twee delen even groot zijn. |
 |
| |
|
|
|
|
| |
a. |
Bereken exact deze
waarde van q. |
| |
|
|
|
|
| |
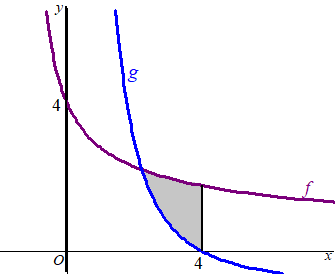
De functie
g is de inverse functie van de functie f . Het
gebied dat wordt ingesloten door de grafiek van f , de
grafiek van g en de lijn met vergelijking x = 4 is
in de figuur hiernaast grijs gekleurd. |
 |
| |
|
|
|
| |
b. |
Bereken de oppervlakte
van dit gebied. Geef je eindantwoord in één decimaal. |
| |
|
|
|
|
| 21. |
Examenvraagstuk
VWO Wiskunde B, 2022-III
De functie f
is gegeven door |
| |
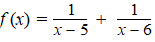 |
| |
|
|
|
|
| |
De functie F
gegeven door F(x) = ln(x2
- 11x + 30) dan een
primitieve van f. |
| |
|
|
|
|
| |
a. |
Bewijs dit. |
| |
|
|
|
|
| |
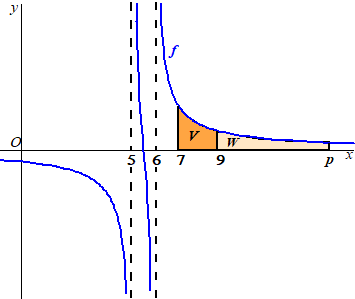
In onderstaande
figuur is de grafiek van f (die uit drie delen bestaat) getekend. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
V is het
gebied begrensd door de grafiek van f, de x-as en de
lijnen met vergelijking x = 7 en x = 9 .
W is het gebied begrensd door de grafiek van f, de x-as
en de lijnen met vergelijking x = 9 en x = p , met
p > 9.
Er is een waarde van p waarvoor de oppervlaktes van V en
W gelijk zijn. |
| |
|
|
|
|
| |
b. |
Bereken exact deze
waarde van p. |
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
 |
| |
|
|
|
|