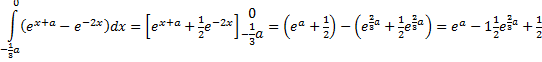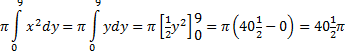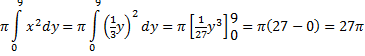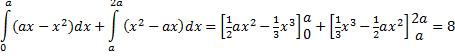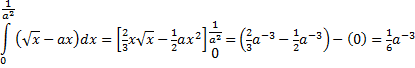|
|||||
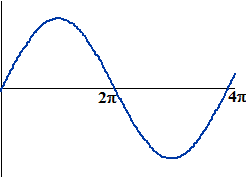
| 1. | De grafiek heeft periode 2π/0,5 = 4π, dus snijdt de x-as bij x = 2π en 4π... | ||||
 |
|||||
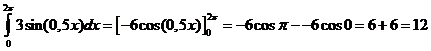 |
|||||
| Dus moet het tweede deel nog oppervlakte 3 geven: | |||||
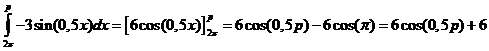 |
|||||
| 6cos(0,5p) + 6
= 3 6cos(0,5p) = -3 cos(0,5p) = -0,5 0,5p = 2/3π ∨ 0,5p = 4/3π p = 4/3π ∨ p = 8/3π De eerste is p = 4/3π |
|||||
| 2. | 2/x
= a geeft x = 2/a Het gebied bestaat uit een rechthoek van 2/a bij a en een deel onder de grafiek tussen x = 2/a en x = a De rechthoek heeft oppervlakte 2, dus het deel onder de grafiek moet oppervlakte 4 hebben. |
||||
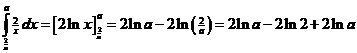 |
|||||
| 4lna - 2ln2 =
4 4lna = 4 + 2ln2 lna = 1 + 1/2ln2 = lne + ln(√2) = ln(e/√2) a = e/√2 = 1/2e√2 |
|||||
| 3. |
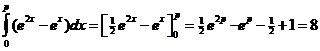 |
||||
| 1/2e2p
- ep - 71/2
= 0 Noem ep zolang a dan staat er a2 - 2a - 15 = 0 (a - 5)(a + 3) = 0 a = 5 ∨ a = -3 De gezochte oplossing is a = 5 en dat geeft ep = 5 dus p = ln5 |
|||||
| 4. | De
oppervlakte van de hele rechthoek is 3b dus de oppervlakte van het deel
tussen de x-as en de grafiek van f moet 1,5b zijn. Een primitieve van f(x) is de functie F(x) = 6 • ln|x + 2| - 3x, dus: |
||||
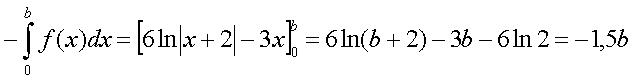 |
|||||
| Invoeren van het linkerdeel en het rechterdeel van deze vergelijking in de GR en de oplossing met INTERSECT vinden geeft b ≈ 5,03 | |||||
| 5. |
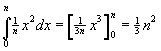 |
||||
|
Dan is de oppervlakte van V gelijk aan n2 - 1/3n2 = 2/3n2 De verhouding is dan 1 : 2 en onafhankelijk van n |
|||||
| 6. |
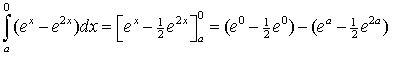 |
||||
|
= 1/2 - ea
+ 1/2e2a
1/2(1 - ea )2 = 1/2 • (1 - ea )(1 - ea) = 1/2 (1 - ea - ea + e2a ) = 1/2(1 - 2ea + e2a ) = 1/2 - ea + 1/2e2a Dat is inderdaad hetzelfde. |
|||||
| 7. |
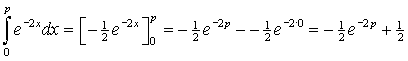 |
||||
| omdat -1/2e -2p altijd kleiner dan nul is (voor p > 0) , is dit dus kleiner dan 1/2. | |||||
| 8. | a. | Het
snijpunt van y = ax met y = 4x -
x2: ax = 4x - x2 ⇒ x2 + ax - 4x = 0 ⇒ x(x + a - 4) = 0 ⇒ x = 0 of x = 4 - a Als x = 4 - a dan is y = ax = a(4 - a) = 4a - a2 |
|||
| b. | Voor de oppervlakte van een vlakdeel tussen twee grafieken moet je de integraal van de bovenste min de onderste nemen: | ||||
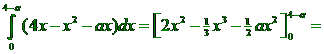 |
|||||
| {2(4 -
a)2 - 1/3(4
- a)3 - 1/2a(4
- a)2 } - {0} Nu kun je alle haakjes wegwerken en van 1/6(4 - a)3 ook, en dan laten zien dat het gelijk is. Het gaat sneller zo: 2(4 - a)2 - 1/3(4 - a)3 - 1/2a(4 - a)2 = (2 - 1/2a) • (4 - a)2 - 1/3(4 - a)3 = 1/2(4 - a) • (4 - a)2 - 1/3(4 - a)3 = 1/2(4 - a)3 - 1/3(4 - a)3 = (1/2 - 1/3)(4 - a)3 = 1/6(4 - a)3 |
|||||
| c. | 4x - x2 = 0 ⇒ x(4 - x) = 0 ⇒ x = 0 of x = 4 | ||||
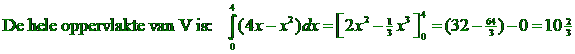 |
|||||
| Dan
moet het bovenste deel dus 51/3
zijn, dus 1/6(4
- a)3 = 51/3 (4 - a)3 = 32 ⇒ 4 - a = (32)1/3 ⇒ a = 4 - 321/3 |
|||||
| 9. |
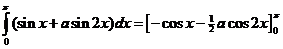 |
||||
| =
(-cosπ - 1/2acos2π)
- (-cos0 - 1/2acos0)
= --1 - 1/2a
- -1 + 1/2a
= 2 En dus is dat onafhankelijk van a |
|||||
| 10. | punt A: f(x) = 0
⇒ -x3 + 3px2
= 0 ⇒ x2(-x
+ 3p) = 0 ⇒ x =
0 Ú x = 3p
Dus A = (3p, 0) de rechthoek: T: f ' (x) = 0 ⇒ -3x2 + 6px = 0 ⇒ 3x(-x + 2p) = 0 ⇒ x = 0 ∨ x = 2p x = 2p geeft y = -(2p)3 + 3p • (2p2) = -8p3 + 3p • 4p2 = -8p3 + 12p3 = 4p3 dus T = (2p, 4p3) De oppervlakte van de rechthoek is dan 3p • 4p3 = 12p4 het grijze gebied: |
||||
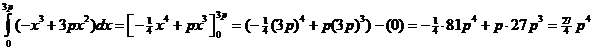 |
|||||
| de verhouding is dan 27/4p4 : 12p4 = 27/4 : 12 = 27 : 48 = 9 : 16 en dat is onafhankelijk van p | |||||
| 11. | Bereken de oppervlakte van het bovenste stuk. Snijpunt van f met de bovenkant van de rechthoek: 1/x = 1/p dus x = p |
||||
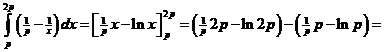 |
|||||
| = 2 -
ln2p - 1 + lnp = 2 - ln2 - lnp - 1 + lnp = 1 - ln2 Dat is inderdaad onafhankelijk van p |
|||||
| 12. |
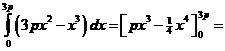 |
||||
| =
p(3p)3 - 1/4(3p)4
= 27p4 - 81/4p4 = 63/4p4 De oppervlakte van het rechterdeel is dan 63/4p4 - 3/4p4 = 6p4 6p4 is inderdaad 8 keer zo groot als 3/4p4 |
|||||
| 13. | snijpunt: e-2x = ex + a ⇒ -2x = x + a ⇒ x = -1/3a | ||||
|
|
|||||
|
Dat is gelijk aan 1/2, dus ea - 1,5e2/3a = 0 ⇒ e1/3a = 1,5 ⇒ 1/3a = ln(1,5) ⇒ a = 3ln(1,5) ≈ 1,216... |
|||||
| 14. | Snijpunt: √x = 1/2√x ⇒ 1/2√x = 0 ⇒ √x = 0 ⇒ x = 0 | ||||
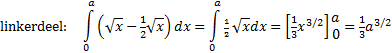 |
|||||
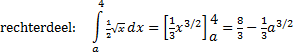 |
|||||
| gelijkstellen:
1/3a3/2
= 8/3
- 1/3a3/2
2/3a3/2 = 8/3 a3/2 = 4 a = 42/3 |
|||||
| 15. | a. |
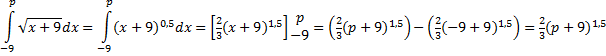 |
|||
| b. | Voor
p = 0 vind je dat de hele oppervlakte van het gebied ingesloten
door de x-as, de y-as en de grafiek van f gelijk is
aan 2/3(0
+ 9)1,5 = 2/3
• 27 = 18 De oppervlakte van V moet dus gelijk zijn aan 18/8 2/3 • (p + 9)1,5 = 18/8 (p + 9)1,5 = 27/8 p + 9 = (27/8)2/3 = 9/4 p = 9/4 - 9 = -63/4 |
||||
| 16. | a. | x2 = 3x ⇒ x = 0 ∨ x = 3 | |||
| parabooldeel omwentelen: | |||||
|
|
|||||
| rechte lijn omwentelen: | |||||
|
|
|||||
| Het vlakdeel heeft inhoud 401/2π - 27π = 131/2π | |||||
| b. | Q = (a , a2 ) dus OQ is de lijn y = ax | ||||
|
|
|||||
| (1/2a3
- 1/3a3 ) - (0)
+ (8/3a3
- 2a3 ) - (1/3a3
- 1/2a3)
= 8 1/6a3 - 0 + 1/3a3 + 1/6a3 = 8 a3 = 8 a = 2 |
|||||
| 17. | Snijpunt: ax = √x ⇒ a2x2 = x ⇒ x = 1/a² ∨ x = 0 | ||||
|
|
|||||
| 1/6a-3
= 102/3 a-3 = 64 a = 1/4 |
|||||
| 18. | de
rechte lijn OP is de lijn y = px de oppervlakte van V is dan: |
||||
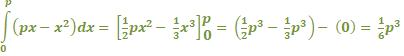 |
|||||
| de
raaklijn in (p, p2) heeft helling
y' = 2x = 2p raakpunt invullen: p2 = 2p • p + b geeft b = -p2 de raaklijn is y = 2px - p2 snijden met de x-as: 2px - p2 = 0 2px = p2 x = 1/2p De oppervlakte van OAP is 1/2 • 1/2p • p2 = 1/4p2 1/4p2 is inderdaad precies gelijk aan 1,5 • 1/6p2 |
|||||
| 19. | |||||
| 20. | a. | De
oppervlakte van de rechthoek is 4q De oppervlakte onder de grafiek moet dus 2q zijn. |
|||
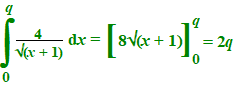 |
|||||
| 8√(q
+ 1) - 8 = 2q 8√(q + 1) = 2q + 8 64(q + 1) = (2q + 8)2 64q + 64 = 4q2 + 32q + 64 4q2 - 32q = 0 4q(q - 8) = 0 q = 0 Ú q = 8 Maar q > 0 dus de oplossing is q = 8 |
|||||
| b. | Voor
g geldt: x = 4/√(y +
1) √(y + 1) = 4/x y + 1 = (4/x)2 y = 16/x² - 1 Snijpunt: Y1 = 16/x² - 1 Y2 = 4/√(x + 1) Calc - intersect geeft X = 2,22.... Y3 = Y2 - Y1 calc - òf(x)dx Y3 Lower Limit x = 2,22.... Upper limit x = 4 Dat geeft oppervlakte 2,10.... Afgerond dus 2,1 |
||||
| 21. | a. | Als
F een primitieve is dan moet gelden F = f F '= 1/(x2 - 11x + 30) • (2x - 11) = (2x - 11)/(x2 - 11x + 30) Neem de beide breuken van f samen: |
|||
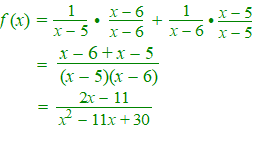 |
|||||
| Dat is inderdaad gelijk aan F ' | |||||
| b. |
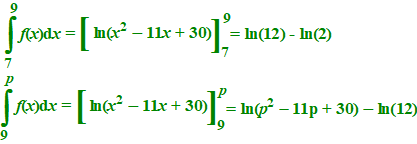 |
||||
| ln(12)
- ln(2) = ln( p2 - 11p + 30) - ln12 ln(12) + ln(12) - ln(2) = ln( p2 - 11p + 30) ln(12 • 12/2) = ln( p2 - 11p + 30) ln(72) = ln( p2 - 11p + 30) p2 - 11p + 30 = 72 p2 - 11p + -42 = 0 (p + 3)(p - 13) = 0 p = -3 ∨ p = 13 De oplossing is p = 13 |
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||