© h.hofstede (h.hofstede@hogeland.nl)  
Maxima en Minima.
Om een top of een dal (maximum of minimum) van een grafiek te vinden ga je als volgt te werk.
   
stap 1:  PLOT de grafiek en zorg dat je het maximum of minimum in beeld hebt.
stap 2: Druk op CALC en kies 3: minimum of 4: maximum
stap 3. Kies door met de cursorpijltjes omhoog of omlaag te gaan de juiste formule  (zie je boven in beeld)
(opm: als er maar één formule in je GR staat hoef je dit uiteraard niet te doen)
stap 4. Je rekenmachine vraagt nu  "Left Bound?"
Ga met de cursor aan de linkerkant van het maximum/minimum staan, en druk op ENTER
stap 5. Je rekenmachine vraagt nu  "Right Bound?"
Ga met de cursor aan de rechterkant van het maximum/minimum staan, en druk op ENTER.
stap 6. Je rekenmachine vraagt nu  "Guess?"
Ga met de cursor (ongeveer) op het maximum/minimum staan en druk weer op ENTER.
Dan verschijnen de coördinaten onder in beeld.
Voorbeeld:  Zoek de coördinaten van het maximum van de grafiek van y = 2x3 - 5x + 8.
 
Het gezochte maximum is ongeveer het punt  (-0.91, 11.04)
 
Nulpunten.
   
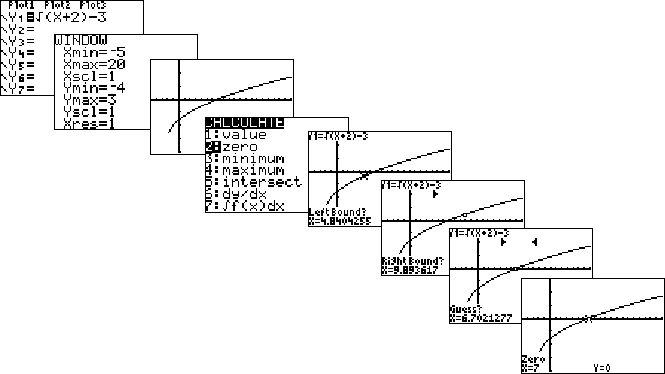
Nulpunten zijn de snijpunten van de grafiek met de x-as. Om precies te zijn: het zijn de x-coördinaten van die snijpunten. Als een nulpunt gevraagd wordt, hoef je alleen de x te noemen (de y is niet nodig, want die is namelijk....NUL natuurlijk!)

Het berekenen van nulpunten met de rekenmachine gaat als volgt:
   
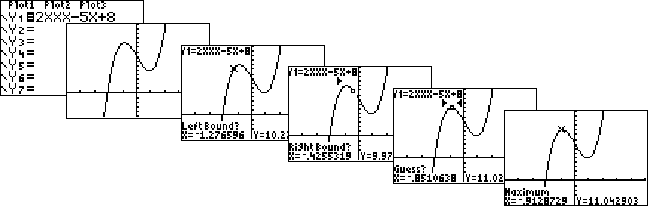
stap 1. Voer de formule in bij Y =     en zorg via WINDOW dat je de nulpunten in beeld hebt.
stap 2. Druk op CALC en kies 2: zero
stap 3. Kies door met de cursorpijltjes omhoog of omlaag te gaan de juiste formule  (zie je boven in beeld)
(opm: als er maar één formule in je GR staat hoef je dit uiteraard niet te doen)
stap 4. Je rekenmachine vraagt nu "Left Bound?"
Ga met de cursor aan de linkerkant van het nulpunt staan, en druk op ENTER
stap 5. Je rekenmachine vraagt nu "Right Bound?"
Ga met de cursor aan de rechterkant van het nulpunt staan, en druk op ENTER
stap 6. Je rekenmachine vraagt nu "Guess?"
Ga met de cursor (ongeveer) op het nulpunt staan en druk weer op ENTER.
Dan verschijnen de coördinaten onder in beeld.
   
Voorbeeld:  Zoek de coördinaten van het nulpunt van de grafiek van y = √(x + 2) - 3
 
De oplossing in 8 etappes:
Het gezochte nulpunt is  x = 7
   
 
 
OPGAVEN
   
1. Bereken de maxima en/of minima van de grafieken van de volgende functies:
       
  a. f(x) = 4x2 - 5x + 8
       
  b. f(x) = 0,5x • 2x
       
  c. f(x) = 0,05x3 - 1,3x2 + 0,6x
       
  d.
       
  e.
   
2. Bereken de nulpunten van de grafieken van de volgende functies:
       
  a. f(x) = 2x5 - 8x3 + 10
       
  b. f(x) = 0,003x3 - 0,12x2 + 0,06x
       
  c. f(x) = √(x + 8) - 0,2x + 2,8
       
  d. f(x) = 2x - 3x
       
  e.
       
  f.
       

© h.hofstede (h.hofstede@hogeland.nl)