Substitutie.

© h.hofstede (h.hofstede@hogeland.nl)

We hebben tot nu toe twee manieren gezien om vergelijkingen met hogere machten dan een kwadraat op te lossen.

eerste manier:
Als er maar één x in de vergelijking staat kun je de balansmethode gebruiken,
en dan gebruiken dat  xn = p  ⇒  x = p1/n   (oppassen met even n).

Voorbeeld:    Los op:  2 • (3x - 4)4 - 5 = 27
Oplossing:   2 • (3x - 4)4 = 32   ⇒  (3x - 4)4 = 16  ⇒  3x - 4 = 161/4 = 2  ∨  3x - 4 = -161/4 = -2
⇒  3x = 6  ∨  3x = 2    ⇒  x = 2  ∨  x = 2/3

tweede manier:
Herleid de vergelijking op nul en ga daarna ontbinden in factoren ("dubbelen zoeken").
Gebruik daarna de eigenschap  A • B = 0  ⇒  A = 0  ∨  B = 0.

Voorbeeld:  Los op:   12x4 = 3x6
Oplossing:   12x4 - 3x6 = 0  ⇒  x4(12 - 3x2 ) = 0  ⇒  x4 = 0  ∨  12 - 3x2 = 0  ⇒  x = 0  ∨  x2 = 4
⇒  x = 0  ∨  x = 2  ∨  x = -2  

Maar het wiskunde-leven is niet altijd zo mooi.
Neem de volgende vergelijking:  x4 - 13x2 + 36 = 0
• De eerste manier hierboven werkt niet, want er zitten twee x-en in de vergelijking en die kun je niet samennemen.
• De tweede manier hierboven werkt niet want er zijn geen "dubbelen" te vinden.

HELAAS.... volgende som dan maar?

Nee, wacht!
Er is nog een laatste truc die in sommige gevallen werkt, en dat is de methode van "substitutie". Dat betekent letterlijk "vervanging" en het gaat als volgt:

x4 - 13x2 + 36 = 0  is hetzelfde als  (x2)2 - 13x2 + 36 = 0
En nu valt het op dat het "blokje" x2 er vaker in staat.  Je kan de opgave lezen als    (...)2 - 13 • (...) + 36 = 0
Laten we dat blokje een andere naam geven:  noem  x2 = p
Dan staat hierboven  p2 - 13p + 36 = 0
En díe is wél op te lossen:  (p - 9) • (p - 4) = 0  ⇒  p = 9  ∨  p = 4
Maar omdat p gelijk was aan x2 moet dus gelden  x2 = 9  ∨  x2 = 4
Daaruit volgt dan tenslotte  x = 3  ∨  x = -3  ∨  x = 2  ∨  x = -2
1. Los op:
a.  x4 + 2x2 - 15 = 0

±√3
f.   6 • (2x - 4)3 = (2x - 4)2 
2 en 25/12
b.  9x2 + x4 + 18 = 0
geen opl.
g.   x8 = 4x4 + 12

±61/4
c.  x4 + 14 = 9x2

±√2  en ±√7
h.   x8 - 5x5 + 4x2 = 0
0 en 1 en 41/3
d.  3x4 - 6x2 = 144

±√8
i.    x7  - x5 - 6x3 = 0

0 en ±√3
e.  x6 + 4x3 = 12

3√-6  en 3√2
j.   x2 (x2 + 5) = 2(x2 - 1) 

geen opl.
     
2. Gegeven is de vergelijking x4 - x2 + p = 0
Maak een grafiek met op de horizontale as de waarde van p en op de verticale as  het aantal oplossingen van deze vergelijking.
     
3. examenvraagstuk VWO Wiskunde B, 1985.

Met domein R\{0}  is gegeven de functie:
     
 

     
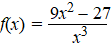  Voor welke p ∈ R heeft  Kf  precies vier punten met de lijn y = px  gemeen?
   

0 < p < 0,75
4. examenvraagstuk HAVO Wiskunde B, 2012.
     
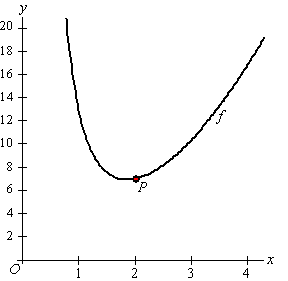
  De functie f is gegeven door f (x) = x2 + 12x -2, 
met  x > 0.
In de figuur hiernaast is de grafiek van f getekend.


Een horizontale lijn snijdt de grafiek van f in de punten A en B. De x-coördinaat van A is 1.
Bereken de x-coördinaat van B. Geef je antwoord in twee decimalen nauwkeurig.

       

3,46
5. Een rechthoekige driehoek heeft schuine zijde 10 en oppervlakte 24.
Bereken de omtrek.
       

24
   
6. Voor welke waarden van a heeft de vergelijking  3x + 31 - x = a minstens één oplossing?
         
         
Het kan natuurlijk ook met gebroken machten....
Neem bijvoorbeeld:     x3  - 6x√x - 16 = 0
Op onze blokjesjacht valt op dat  x√x = x1 • x0,5 = x1,5   en x3 is precies daar het kwadraat van.
Noem daarom  p = x√x = x1,5   dan staat er  p2 - 6p - 16 = 0
Dat geeft  (p + 2)(p - 8) = 0  ⇒  p = -2  ∨  p = 8
x1,5 = -2 heeft geen oplossing en  x1,5 = 8 geeft  x = 81/1,5 = 82/3 = 4
7.  Los algebraïsch op, en geef indien nodig je antwoorden in twee decimalen nauwkeurig.:
a.   x√x + x3 = 30 

2,92
e.  √(x + 1) + x + 1 = 20

15
b.   x - 4√x + 4 = 0  

4
f.   2√x = x - 24 

36
c.   2x5 = x2√x + 10

1,44
g.  x3√x - 3x2 = 10√x

0 en 2,92
d.   x3/4 = x√x - 6

4,33
h.   22x - 10 • 2x + 16 = 0

1 en 3
  
8. Los de opgaven b, e en f   hierboven ook op met de methode van "isoleren, kwadrateren, controleren".
Kijk of je dezelfde antwoorden als hierboven vindt.
   
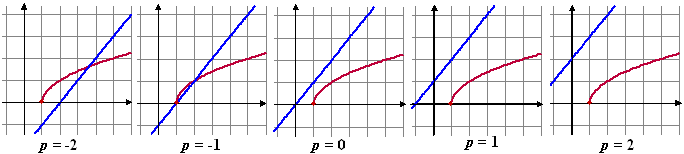
9. Gegeven is de familie van functies   fp (x) = x +  p  en  ook de functie  g(x) = √(x - 1)
Hieronder staan voor een  aantal waarden van p de grafieken van fp en g getekend.

Het valt natuurlijk meteen op dat de grafieken van fp en g soms twee snijpunten hebben, soms één en soms geen.
Het moment van geen snijpunten meer begint zo te zien ergens tussen p = -1 en p = 0.
De vraag is natuurlijk:  "Bij welke p?"
a. Toon aan dat je, om een eventueel snijpunt te berekenen, de vergelijking  x - 1 - √(x - 1) + p + 1 = 0
moet oplossen.
   
b. Verander door een handig blokje te kiezen de vergelijking uit vraag a)  in een kwadratische vergelijking.
 

q2 - q + p - 1 = 0
c. Bepaal met de vergelijking uit b) voor welke p-waarden er één snijpunt zal zijn.
 

p = -3/4
   

© h.hofstede (h.hofstede@hogeland.nl)