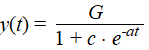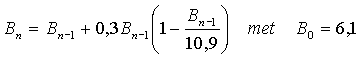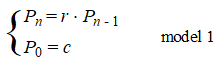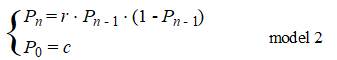Logistische groei.

© h.hofstede (h.hofstede@hogeland.nl)
   
Bij logistische groei is de toename per stap evenredig met het aantal  un-1 en ook met de groeiruimte  G - un - 1 .
Je ziet dat soort groei vaak in de biologie bij toename van aantallen diersoorten.
In het begin, als er nog genoeg ruimte is,  neemt het aantal dieren van een bepaalde soort ongeveer exponentieel toe. Immers als elk exemplaar een gemiddeld aantal nakomelingen produceert, dan is "hoeveel erbij komen" evenredig met "hoeveel er zijn", en dat geeft exponentiële groei.
Maar als er meer en meer exemplaren komen, dan wordt de leefruimte een beperkende factor, bijvoorbeeld door voedselgebrek. Stel dat er plaats is voor maximaal G exemplaren, dan is de beschikbare ruimte evenredig met aan G - un.
Dat geeft als recursievergelijking:
   

un =  un - 1 + c • un - 1 • (G -  un - 1) 

   
Het levert een S-vormige grafiek op, ongeveer zoals hiernaast.
De algemene vergelijking van logistische groei ziet er als volgt uit:
 

 

Met G de grenswaarde en c en a constanten, afhankelijk van de beginwaarde en de groeisnelheid.

(de afleiding van deze formule is nogal lastig, daarvoor moet je kennis hebben van differentiaalvergelijkingen. Met name van deze les.)

   
Hoe herken ik zulke groei?  
   
Logistische groei voldoet aan een erg eenvoudige regel:
   

   
Met formules betekent dat:   
   

   
Het is eenvoudig in te zien dat dit inderdaad leidt tot een formule van de eerder gegeven vorm, kijk maar:
Dat is inderdaad de eerder gegeven formule, met B = c  en   g = e-a.
   
voorbeeld.

De volgende tabel voldoet aan logistische groei met een grenswaarde van G = 1200.
Toon aan dat dat inderdaad zo is, en geef een formule voor N(t)
   
t 0 1 2 3 4 5 6 7 8 9 10
N(t) 63 88 122 167 225 298 385 483 589 695 796
   
oplossing:
vul de tabel aan met een rij 1200 - N  en een rij  (1200 - N)/N:
   
t 0 1 2 3 4 5 6 7 8 9 10
N(t) 63 88 122 167 225 298 385 483 589 695 796
1200 - N 1137 1112 1078 1033 975 902 815 717 611 505 404
(1200 - N)/N 18,05 12,64 8,84 6,19 4,33 3,03 2,12 1,48 1,04 0,73 0,51

De groeifactoren van de onderste rij zijn  12,64/18,05,  8,84/12,64,  6,19/8,84, 4,33/6,19, ...enz.
Dat is steeds 0,7.
Die onderste rij vertoont dus exponentiële groei met B = 18 en g = 0,7.
   
  OPGAVEN
   
1. De volgende tabel beschrijft logistische groei met een grenswaarde van 5000.
       
 
t 0 5 10 15 20
A(t) 50 570 3116 4775 4982
     
  a. Toon aan dat de groei inderdaad logistisch is  
       
  b. Geef een formule voor A(t)  
     

5000/(1+100•0,6t)
2. Kijk nog eens naar de vergelijking voor logistische groei:
       
 

       
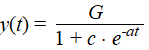  a. Toon aan dat y stijgt als  a  positief is.
       
  b. Iemand beweert:  "c is het aantal keer dat de beginpopulatie er in het begin nog bij moet komen om de grenswaarde G te bereiken".
Toon aan dat dat inderdaad zo is.
       
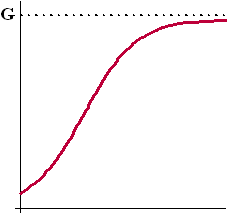
  De S-kromme is een symmetrische kromme.
Omdat y varieert tussen 0 en G zal het buigpunt liggen bij y = 0,5G
       
  c. Druk de t-coördinaat van het buigpunt uit in c en a.
     

t = (lnc)/a
   
3. De volgende tabel geeft de resultaten van een studie door de Verenigde Naties (New York Times, 17 november 1995) waaruit blijkt dat de groei van de wereldbevolking aan het afnemen is. De tabel geeft aan in welk jaar voor het eerst een bepaalde grootte van de wereldbevolking bereikt zal worden. Er blijkt sprake te zijn van logistische groei met G = 11,5 miljard
       
 
jaar 1927 1960 1974 1987 1999 2011 2025 2041 2063
wereldbevolking (in miljarden) 2 3 4 5 6 7 8 9 10
       
  Noem t = 0 in 1900 en onderzoek welke vergelijking het best past bij de grootte van de wereldbevolking als functie van t
     

11,5/(1 + 12,8e-0,0266t)
       
4. Neem de volgende vergelijking voor logistische groei:
 

       
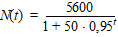  a. Onderzoek voor welke waarden van t er (ongeveer) sprake is van exponentiële groei. Bereken de waardes van g in één decimaal nauwkeurig.
       
  b. De grafiek is weer een S-kromme. Onderzoek met je GR bij welke t de grafiek overgaat van toenemende stijging naar afnemende stijging.
     

t = 76
       
5. Neem aan dat een vrouw logistisch groeit vanaf haar geboorte (50 cm lang) tot aan haar volwassen lengte (140 cm lang). Als zij op 15 jarige leeftijd 95% van haar volwassen lengte heeft bereikt, op welke leeftijd groeit zij dan het snelst?
     

2,5 jaar
       
6. Examenvraagstuk VWO Wiskunde A, 2004

Onlangs stelde iemand het volgende model op om een ruwe schatting van de toekomstige wereldbevolking te maken:
 

       
 

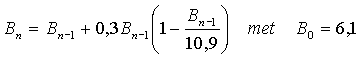Hierin is Bn de wereldbevolking in miljarden mensen en n het aantal eenheden van 10 jaar na 2000. Dus B0 is de wereldbevolking in 2000, B1 de wereldbevolking in 2010, enzovoort.
De volgende vragen hebben betrekking op dit model.

Volgens dit model zal de wereldbevolking op de lange duur een grenswaarde bereiken.
       
  a. Onderzoek, of de wereldbevolking volgens dit model in 2050 minder dan 10% van deze grenswaarde verwijderd zal zijn.
       
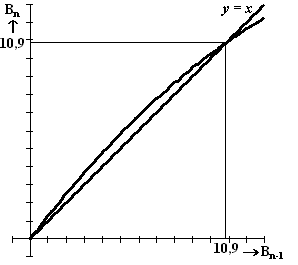
  Bij dit model kan een webgrafiek gemaakt worden. Zie de figuur hieronder.
       
 

       
  b. Teken de eerste drie stappen (dus van B0 tot en met B3) van de webgrafiek in deze figuur. Licht je werkwijze toe.
       
  Of het model de toekomstige ontwikkeling redelijk beschrijft, moeten we nog afwachten. Wel kunnen we controleren of het model in overeenstemming is met de ontwikkeling vóór 2000. Zo is te berekenen hoe groot volgens de formule voor Bn de wereldbevolking in 1990 was.
       
  c. Voer deze berekening uit.
       
7. Examenvraagstuk VWO Wiskunde A, 2023-II

In de 18e eeuw werd algemeen aangenomen dat de toename van een populatie dieren kan worden beschreven met behulp van een meetkundige rij. Een model uit die tijd is:
       
 

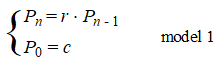  In dit model geldt:
  - Pn is de populatiefractie na n jaar. Dat is de grootte van de populatie als deel van de maximale populatie. Pn is dus een getal tussen 0 en 1.
  - c is de startpopulatiefractie. Ook dit getal wordt uitgedrukt als een deel van de maximale populatie
(en dus geldt 0 < c < 1).
  - r is de reproductiefactor: een getal dat aangeeft hoe snel een populatie zich per jaar uitbreidt.
       
  Neem aan dat in een bepaald bosrijk gebied een populatie van 165 vossen leeft. De reproductiefactor van de vossen in dit gebied is 1,28 en in het gebied is plaats voor maximaal 500 vossen.
       
  a. Bereken met behulp van model 1 na hoeveel jaar dit maximale aantal bereikt zal zijn.
     

5 jaar
  In model 1 wordt ervan uitgegaan dat een populatie altijd even snel groeit. Dit komt echter niet overeen met de werkelijkheid: als de populatie groeit wordt de ruimte per dier namelijk steeds kleiner, waardoor het moeilijker wordt om voedsel te vinden. Hierdoor zal een populatie steeds minder snel gaan groeien naarmate deze toeneemt.

Een verbeterde versie van model 1 is het logistische model:
       
 

       
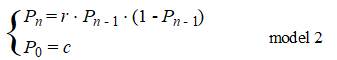  De variabelen in dit model hebben dezelfde betekenis als in model 1.

De Oostvaardersplassen is een natuurgebied in de buurt van Lelystad. In 2020 leefden er in dit gebied een groot aantal edelherten. Door dit grote aantal konden andere diersoorten, voornamelijk vogels, zich niet meer goed ontwikkelen. Mede daarom wordt sinds 2021 de populatie door het afschieten van de dieren stabiel gehouden op 500 edelherten.

Neem aan dat er maximaal 2000 edelherten in de Oostvaardersplassen kunnen leven.
Er geldt vanaf 2021 dat r = 1,58 en c = 0,25 .
       
  b. Bereken met behulp van model 2 hoeveel edelherten er in de periode 2021-2023 bij zouden komen als er geen dieren zouden worden afgeschoten.
     

158/159
  In de rest van deze opgave gaan we bekijken hoe model 2 zich gedraagt bij verschillende waarden van r. Als je voor r een getal tussen de 0 en 1 invult, dan nadert Pn voor iedere startwaarde c (met 0 < c < 1) naar 0. Je kunt dat beredeneren met de formule voor Pn .
       
  c. Geef een redenering waaruit blijkt dat wanneer r tussen de 0 en 1 is, Pn altijd naar 0 nadert.
       
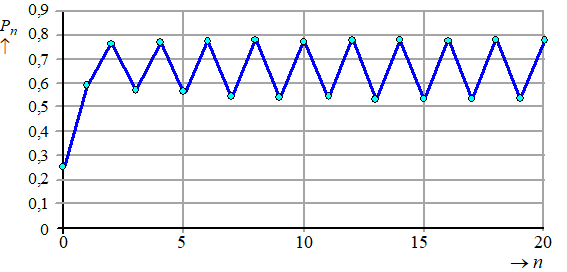
  Voor waarden van r groter dan 1 wordt het model erg onvoorspelbaar.
       
 

       
  In de figuur is de grafiek getekend voor r = 3,15 en c = 0,25 . Er is te zien dat de waarde van Pn op den duur heen en weer gaat springen tussen twee vaste waarden.
       
  d. Onderzoek tussen welke twee waarden Pn heen en weer gaat springen voor r = 3,15 en c = 0,25 . Geef deze waarden in twee decimalen.
     

0,78/0,53
     

© h.hofstede (h.hofstede@hogeland.nl)