Logaritmisch differentiëren.

© h.hofstede (h.hofstede@hogeland.nl)
       
De afgeleide van lnx is erg eenvoudig:
 
f(x) = lnx   ⇒   f '(x) = 1/x
   

Omdat verder geldt dat    ln(ab) = lna + lnb   en   lnab  =  blna   kun je vrij ingewikkelde functies met machten en producten vaak met behulp van logaritmen makkelijker schrijven en daarna vrij eenvoudig differentiëren.

Hier zie je hoe het werkt:
       
Voorbeeld:
Neem eerst van beide kanten de natuurlijke logaritme, en vereenvoudig die met beide ln-regeltjes hierboven.
Dat geeft:    lny = 3lnx + 1/2ln(x2 - 1) - 3ln(2 - 4x)
Differentieer nu impliciet (met als variabele x), dat geeft:    1/y • y'   = 3/x  + x/(x2 - 1) + 12/(2 - 4x)
Breng y naar de nadere kant :    y'   = y • ( 3/x  + x/(x2 - 1) + 12/(2 - 4x))
Maar voor die y kun je de oorspronkelijke uitdrukking weer invullen:
       
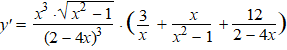De stappen bij logaritmisch differentiëren zijn dus altijd deze vier:
       
1.  neem de  natuurlijke logaritme van beide kanten van y = f(x).
2.  impliciet differentiëren
3.  dy/dx  maken
4.  y weer vervangen door de  oorspronkelijke formule.  
       
Mooi hé?.......
       
           
1. Bereken de afgeleides van de volgende functies:
           
  a.   c. f(x) = x1/3·(x - 1)8 ·Ö(2 + 2x)  
             
  b.   d.  
           
2. Toon met logaritmisch differentiëren aan dat de afgeleide van y = xn  gelijk is aan  y' = nxn - 1
           
         

© h.hofstede (h.hofstede@hogeland.nl)