limieten van machten


Limieten van machten.	© h.hofstede (h.hofstede@hogeland.nl)

Met een aantal machten in een limiet waarvan sommigen naar 0 gaan en sommigen naar ∞ en sommigen naar -∞ is het niet altijd even makkelijk te zien wat het resultaat zal zijn.
Een beste tactiek is vaak:

Deel door de hoogste macht die "een probleem geeft"

Ok, als ik dit zelf nog eens nalees denk ook ik: "Wat bedoelt de schrijver daar in hemelsnaam mee?"
Misschien dat een voorbeeld duidelijk maakt wat ik bedoel.

Voorbeeld 1.

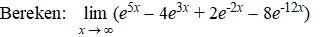Daar staan vier termen achter die limiet. Als je van al die termen apart bekijkt waar ze naar toe gaan als x naar oneindig gaat, dan krijg je ∞ - ∞ + 0 + 0
Die laatste twee zijn duidelijk te verwaarlozen, maar die eerste twee die "geven een probleem": dat is nogal onduidelijk wat daar uit komt.
Deel alles door de hoogste macht van die twee. Dat is in dit geval e^5x.
Dan hou je over 1 - 4e^-2x + 2e^-7x - 8e^-17x
Dat gaat allemaal naar nul, behalve die eerste term.

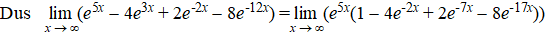Al die negatieve machten gaan naar nul, en die e^5x gaat naar ∞ dus er komt ∞ uit

Voorbeeld 1 nét ietsje anders.

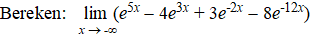Lijkt er nogal op, vind je niet?
Het enige verschil met de vorige is dat x nu naar negatief oneindig gaat.
Nu krijg je als je al de termen in de limiet bekijkt achtereenvolgens 0 - 0 + ∞ - ∞
Het zijn nu de laatste twee die "problemen geven".
Daarom deel je nu alles door de hoogste macht van die laatste twee ("hoogste" betekent in dit geval het "verst van nul af", dus dat is e^-12x).
Dat geeft:

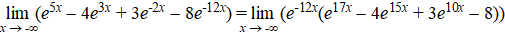Nu gaan alle positieve machten naar nul, en die e^-12x gaat naar ∞ dus er komt -8 • ∞ = -∞ uit.

Kijk naar de hoogste macht van de noemer!

Bij dat buiten haakjes halen gaat het alleen om de "hoogste" macht (kan dus ook meest negatieve macht zijn) van de noemer.

Voorbeeld 2.

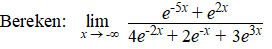Als je naar de noemer kijkt gaan de eerste twee temen naar ∞ en de laatste naar nul. Het gaat dus om die eerste twee, dus we halen e^-2x buiten haakjes (die macht ligt het verst van nul af):

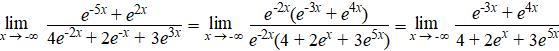De noemer gaat nu naar 4 + 0 + 0 = 4 en de teller gaat naar ∞ + 0 = ∞ dus de hele breuk gaat ook naar ∞

Waarom alleen maar machten van e ?

Dat komt omdat je alle andere machten altijd kunt herleiden tot een macht van e. Het getal e is een soort "basismacht" voor wiskundigen.
Als je bijvoorbeeld hebt 2^x dan kun je daar makkelijk van maken (e^ln2)^x = e^x^ln2 ≈ e^0,69x

Bereken de volgende limieten:

1¹/₃

∞