| |
 |
|
Nog meer limieten... |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
|
|
|
| In de vorige les heb
je gezien wat een "limiet" is en hoe je met je GR meestal wel kunt
bepalen wat er uitkomt. |
Maar de zaken kunnen soms wat
gecompliceerder zijn.....
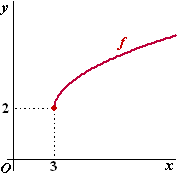
Probleem 1.
Neem de grafiek hiernaast, van f(x) = 2 +
√(x - 3).
Stel dat je daarvan de limiet van x naar 3 wilt berekenen.
Dan lukt dat niet door achtereenvolgens x = 2,5 en 2,9 en 2,99 en
2,999 enz. in te vullen. Aan de grafiek zie je wel dat de functie daar
helemaal niet bestaat!
Je kunt alleen wel x = 3,5 en 3,1 en 3,01 en 3,001 enz. invullen, want daar
aan de rechterkant van 3 bestaat de grafiek wél. Aan die waarden zie je dat
de limiet gelijk is aan 2.
In zulke gevallen geven we nauwkeuriger in de limiet aan vanaf welke
kant je moet rekenen. Dat ziet er zó uit: |
 |
| |
|
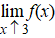 |
Spreek uit: "de
limiet van de onderkant naar 3", en dat betekent dat je van getallen
kleiner dan 3 naar 3 zelf toegaat. (Dus 2,9 en 2,99 en 2,999 enz.)
Deze limiet bestaat in bovenstaand voorbeeld niet.
We spreken ook wel van de linkerlimiet (in de grafiek kom
je van de linkerkant) |
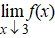 |
Spreek uit: "de
limiet van de bovenkant naar 3", en dat betekent dat je van getallen
groter dan 3 naar 3 zelf toegaat. (Dus 3,1 en 3,01 en 3,001 enz.)
Deze limiet is in bovenstaand voorbeeld gelijk aan 3.
We spreken ook wel van de rechterlimiet (in de grafiek kom
je van de rechterkant) |
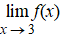 |
Deze notatie is
onnauwkeuriger en mag je alleen gebruiken als de beide vorige limieten
dezelfde waarde opleveren. Dus alleen als de linkerlimiet en de
rechterlimiet dezelfde waarde opleveren mag je spreken over
"DE" limiet. In
bovenstaand voorbeeld bestaat deze limiet dus niet!!! |
| |
|
|
|
| Voorbeeld. |
|
|
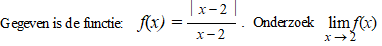 |
Op de eerste plaats
zie je dat 2 invullen niet kan, want dat levert 0/0 op.
Als je waarden kleiner dan 2 invult krijg je bijvoorbeeld:
f(1,9) = -1 en f(1,99) = -1 en f(1,999)
= -1 dus dat lijkt gelijk te zijn aan -1.
Als je waarden groter dan 2 invult krijg je bijvoorbeeld;
f(2,1) = 1 en f(2,01) = 1 en f(2,001) = 2
dus dat lijkt gelijk te zijn aan 1.
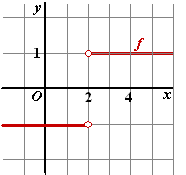
Conclusie: |
 |
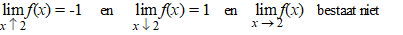 |
| Aan de grafiek
hiernaast zie je duidelijk wat er aan de hand is. |
| |
|
|
|
|
Probleem 2. |
| |
|
|
|
| Soms komt er gewoon
niets uit! |
|
|
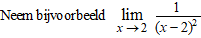 |
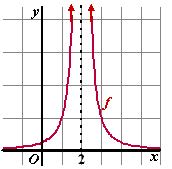 |
Als je waarden steeds
dichter bij 2 neemt, dan worden de berekende functiewaarden groter en
groter, kijk maar:
f(1,9) = 100, f(1,99) = 10000, f(1,999)
= 1000000, enz.
en ook van rechts: f(2,01) = 10000, f(2,001)
= 1000000, enz.
In zo'n geval zeggen we dat de limiet "oneindig" is (symbool
¥ ). Maar
oneindig is natuurlijk geen getal. Met "de limiet is oneindig" wordt
daarom bedoeld: "je kunt de uitkomst zo groot krijgen als je maar wilt".
In de grafiek hiernaast zie je wat er aan de hand is. |
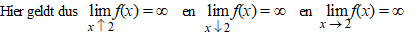 |
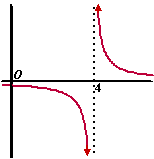 |
| In de onderste
grafiek hiernaast zie je een geval waarin geldt: |
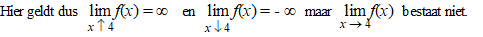 |
| |
|
|
|
|
|
|
Continuïteit. |
| |
|
|
|
| De volgende regel
vind ik één van de mooiste en duidelijkste afspraken over een wiskundig
begrip: |
| |
|
|
|
| Een functie is continu als je de grafiek
ervan kunt tekenen zonder je potlood van het papier te
halen. |
|
| |
|
|
|
Duidelijk! Je snapt
meteen wat er bedoeld wordt, toch?
Helaas moeten formele wiskundigen deze prachtige afspraak weer bederven
omdat ze hem niet precies genoeg vinden! |
| |
|
|
|
|
Zeikerds! |
 |
| |
|
|
|
| De officiële definitie van het continu zijn van een functie is
(helaas) vervangen door: |
| |
|
|
|
|
Een functie f is continu
in punt x = a als: |
| |
|
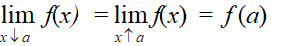
|
|
|
| |
|
|
|
| Ik hoop dat je ziet
dat dat eigenlijk dezelfde afspraak is! |
| |
|
| • |
Als de linkerlimiet
en de rechterlimiet beiden gelijk zijn aan f(a) dan loopt
de grafiek van beide kanten naar dat punt (a, f(a)) toe. |
| • |
Als de limiet ook nog
gelijk is aan f(a) dan zit daar dus geen gaatje, maar
bestaat de grafiek daar ook nog. |
| |
Samen garandeert dat,
dat je bij punt x = a je potlood niet van het papier hoeft af te
halen.
Verder noemen die zeikerds een functie continu op een heel stuk, als hij
continu is in elk punt van dat stuk: |
| |
|
|
|
|
f(x) is continu op interval [a,
b] als f(x) continu is in elk punt
van dat interval. |
|
| |
|
|
|
| Kortom: dan kun je de
grafiek tekenen op [a, b] zonder je potlood van het papier te
halen. |
| |
|
|
|
| Voorbeeld. |
 |
De functies f(x)
= x2 en f(x) = ex
zijn continu, dus voor x< 0 en x > 0 zal deze
gecombineerde functie ook continu zijn.
Het enige spannende is de continuïteit voor x = 0. |
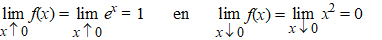 |
| Die limieten zijn
niet gelijk, dus de functie is niet continu voor = 0. |
| |
|
|
|
| |
|
|
|
|
|
|
|
| 3. |
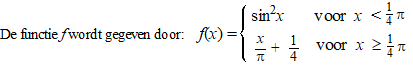 |
| |
Onderzoek de continuïteit van f. |
| |
|
|
|
|
|
|
|
| 4. |
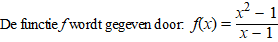
|
| |
Onderzoek de continuïteit van f. |
| |
|
| 5. |
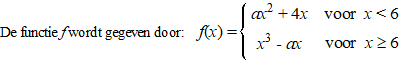 |
| |
Voor welke waarde(n) van a is deze
functie continu? |
| |
|
| |
|
| 6. |
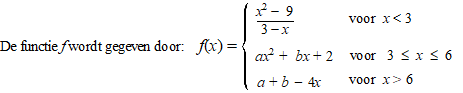 |
| |
Voor welke waarden van a en b
is deze functie continu? |
| |
|
| |
|
| 7. |
De functie g wordt gegeven door: |
| |
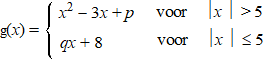 |
| |
Bereken de waarden van p en q
waarvoor deze functie continu is. |
| |
|
|
|
Links- en Rechtscontinu. |
| |
|
|
|
Voor het continu zijn
van een functie was het nodig dat zowel de rechterlimiet als de
linkerlimiet naar de functiewaarde zelf naderden.
Het kan natuurlijk ook voorkomen dat slechts één van beiden naar de
functiewaarde nadert en de andere niet (of zelfs niet bestaat) In zo'n
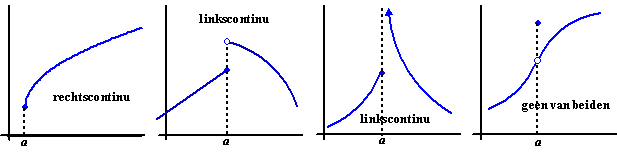
geval noemen we de functie linkscontinu
(linkerlimiet nadert naar f(a)) of
rechtscontinu (rechterlimiet nadert naar f(a)).
Hieronder zie je een paar voorbeelden. |
| |
|
|
|
|
 |
| |
|
|
|
|
Ophefbaar discontinu |
| |
|
|
|
Een functie heet
"ophefbaar discontinu" als er "een gaatje in zit".
Dat betekent in wiskundetaal dat bij de waarde x = a
de linkerlimiet wél gelijk is aan de rechterlimiet, maar dat ze niet
gelijk zijn aan de functiewaarde f(a). Dat
kan zijn omdat f(a) niet bestaat of omdat f(a)
gewoon een andere waarde heeft.
Zoiets dus: |
| |
|
|
|
|
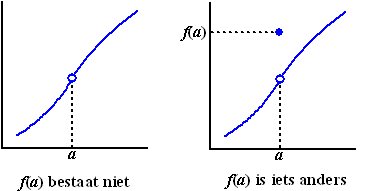 |
| |
|
|
|
In zulke gevallen kun
je gemakkelijk een functie vinden die overal precies gelijk is aan f(x)
maar die het gaatje opvult.
Het gaatje dat je moet toevoegen heet de continumakende waarde
en de nieuwe functie wordt meestal aangegeven met f * |
| |
|
|
|
|
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
| |
|
|
|