| |
 |
|
De regel van l'Hôpital. |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
|
|
|
Onbepaalde vormen.
Als je een limiet probeert te berekenen vul je eigenlijk eerst altijd de
waarde van x maar eens in. Je weet immers maar nooit...
misschien komt er "gewoon" wat uit... Alhoewel, als dat zo is, dan zou
het wel geen opgave zijn trouwens!
Bijna altijd krijg je er een waarde uit die "onbepaald" is. Dat zijn dan
meestal twee delen die elkaar "tegenspreken" zoals in deze voorbeelden: |
|
|
|
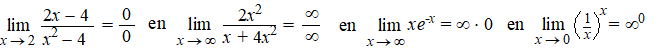 |
| |
|
|
|
Die ingevulde waarden
bestaan allemaal uit twee delen die elkaar tegenwerken.
Bijvoorbeeld van 0/0 wil die bovenste 0 er nul van
maken, maar die onderste 0 wil er oneindig van maken.
Van ∞/∞
is het net andersom: die bovenste maakt het oneindig groot, die
onderste wil er nul van maken.
Dit soort vormen heten "onbepaalde vormen", in tegenstelling tot sommige
andere vormen waarvan meteen duidelijk is wat de limiet wordt. Hier zijn
er nog een paar: |
| |
|
|
|
|
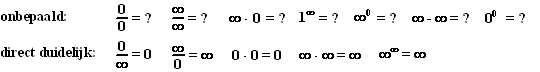 |
| |
|
|
|
| Daarbij moet je alle
getallen als 0, 1, ∞
uiteraard lezen als "gaat naar". |
|
Nou heeft de Fransman
l'Hôpital voor twee van die onbepaalde vormen een handige regel
gevonden. Zelfs handiger dan de meeste lessen over limieten hiervoor!
Hij bedacht het volgende:
| |
|
In de gevallen: |
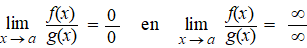 |
|
geldt: |
|
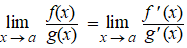 |
|
|
|
 |
| |
|
|
|
Daarbij mag a
zelfs ∞ of
-∞ zijn!!
De regel geldt voorlopig in deze twee gevallen, maar we zullen straks
zien dat veel andere gevallen zijn te herleiden tot één van deze beiden.
Eerst maar even een paar voorbeeldjes van dit geweldig handige regeltje
in werking. De volgende limieten kon je met de theorie van de vorige
lessen ook al wel uitrekenen, maar ze zijn nu gewoon veel makkelijker
geworden. |
| |
|
|
|
| Voorbeeld
1. De vorm 0/0 |
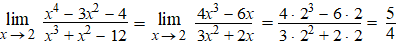 |
| |
|
|
|
| Voorbeeld
2. De vorm ∞/∞ |
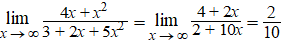 |
| Hier is de regel
zelfs twee keer toegepast. Eerst de afgeleides, maar dat gaf weer ∞/∞
dus daarna gewoon wéér de afgeleides.
Geen enkel probleem! |
| |
|
|
|
| Maar de regel van l"Hôpital
maakt het ook mogelijk limieten te berekenen die we eerst niet konden,
kijk maar: |
| |
|
|
|
| Voorbeeld
3. Een nieuwe limiet! |
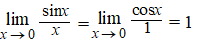 |
| |
|
|
|
|
Producten herleiden. |
| |
|
|
|
| Als de limiet niet
een breuk f/g is,
maar een product f • g dan kun je op de volgende
twee manieren die veranderen in wél een breuk: |
|
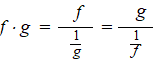 |
| |
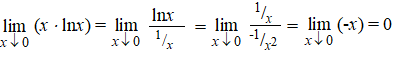 |
| In de eerste stap is
van xlnx een breuk gemaakt, in de tweede stap
is l'Hôpital gebruikt. De limiet moest wel van de bovenkant naar nul,
omdat anders lnx niet bestaat (maar dat had je natuurlijk al lang
door). |
| |
|
|
|
Soms moet je wel een
beetje handig kiezen. Neem de limiet van x
→ -∞
van x • ex .
Als je die x gaat schrijven als 1/x
in de noemer, dan blijf je alsmaar door "L'Hôpitallen", kijk maar: |
|
|
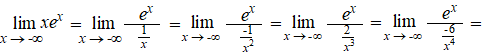 |
| |
|
|
|
Dat schiet niet op....Het
wordt alleen maar erger.....
Maar als je ervoor kiest om ex in de
noemer te zetten in plaats van die x, dan gaat het allemaal een
stuk soepeler: |
| |
|
|
|
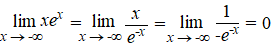 |
| |
|
|
|
|
Machten herleiden. |
| |
|
|
|
We hebben van de
onbepaalde vormen nog over 00 en
∞0
en dat soort machten.
Die vorm kun je op de volgende manier handig anders schrijven: |
| |
|
|
|
|
|
| |
|
|
|
Dat is nogal logisch
natuurlijk, maar het helpt wel om dit soort limieten te berekenen.
Het werkt als volgt: |
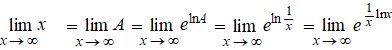 |
Bij de laatste stap
is gebruikt dat ln(xp) = plnx.
Maar de limiet van die macht kun je apart met l' Hôpital berekenen: |
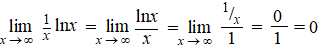 |
| Dus uit de
oorspronkelijke limiet komt e0 = 1 |
| |
|
|
|
| |
|
|
|
|
|
|
|
| 1. |
Bereken de volgende limieten: |
| |
|
|
|
|
|
|
|
| |
a. |
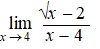 |
|
e. |
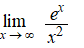 |
|
|
| |
|
|
|
|
|
|
|
| |
b. |
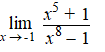 |
|
f. |
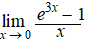 |
|
|
| |
|
|
|
|
|
|
|
| |
c. |
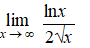 |
|
g. |
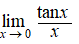 |
|
|
| |
|
|
|
|
|
|
|
| |
d. |
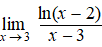 |
|
h. |
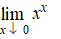 |
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|
|
 |
| |
|
|
|