 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
Gewoon een leuke eigenschap....
- je hebt er verder niets aan
trouwens- |
| |
|
|
|
Neem een willekeurige derdegraads
functie die drie nulpunten heeft.
Laten we zeggen de nulpunten x = a en x = b en x = c.
Dat zijn dus de snijpunten met de x-as.
Dan geldt de volgende verbazingwekkende eigenschap: |
| |
|
|
|
|
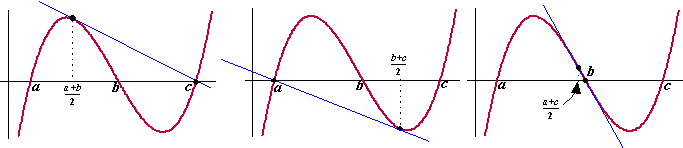
Als je midden tussen twee nulpunten een raaklijn aan de grafiek tekent,
dan gaat die raaklijn door het derde nulpunt! |
|
| |
|
|
|
Leuk toch?
Hieronder zie je wat er aan de hand is: |
| |
|
|
|
|
 |
| |
|
|
|
In het linkerplaatje is de
raaklijn midden tussen a en b getekend, in het
middenplaatje tussen b en c en in het rechterplaatje
tussen a en c. Al die raaklijnen gaan door het derde
nulpunt. Tenminste dat zegt onze stelling.....
Het bewijs. |
| |
|
|
|
Noem de raaklijn de lijn y
= px + q en de vergelijking van de
derdemachtsfunctie f(x).
Midden tussen x = a en x = b zit
x = 1/2a
+ 1/2b
Als de lijn y = px+ q de functie f(x) raakt
in x = 1/2a
+ 1/2b
dan heeft de vergelijking f(x) = px
+ q daar een dubbele oplossing (anders zou het niet raken
zijn, maar snijden).
Dat betekent dat de vergelijking f(x)
- px - q = 0 de oplossingen (1/2a
+ 1/2b,
1/2a
+ 1/2b,
X ) heeft.
Laten we nu naar de nulpunten van een algemene derdegraads-vergelijking
met drie nulpunten (a, b, c) kijken.
Die is dan te schrijven als (x - a)(x - b)(x
- c) = 0
Haakjes wegwerken geeft x3 - x2(a
+ b + c) + x(ab + bc + ac)
- abc = 0
Wat een toeval: de x-coŲrdinaten van de nulpunten zijn
samen precies wat er bij x2 staat! |
| |
|
|
|
|
de x-coŲrdinaten van de
nulpunten zijn samen precies de coŽfficiŽnt van x2 |
|
| |
|
|
|
Maar de groene regel hierboven
heeft een vergelijking f(x)
- px - q = 0 dus die heeft bij x2
precies hetzelfde staan als de vergelijking f(x) = 0.
Dat
px - q verandert daar namelijk niks aan....
ē De groene vergelijking heeft de nulpunten
(1/2a
+ 1/2b,
1/2a
+ 1/2b,
X )
ē f(x) heeft de nulpunten (a,
b, c)
Als je ze allemaal optelt krijg je de coŽfficiŽnt van x2
en die is gelijk, dus moet gelden:
1/2a
+ 1/2b
+ 1/2a
+ 1/2b
+ X = a + b + c
Daaruit volgt kinderlijk eenvoudig dat X = c
Die raaklijn gaat dus inderdaad door het derde nulpunt. |
 |
| |
|
|
|
Het algemenere geval.
Een derdegraadsfunctie waarvan x3 de coŽfficiŽnt 1
heeft kun je altijd schrijven als y = (x -
a)(x - b)(x - c)
De nulpunten zijn x = a en x = b
en x = c
Je kunt dat zien als een parabool y = (x - a)(x
- b) vermenigvuldigd met een rechte lijn y = x
- c
Laten we beginnen met de parabool y = (x - a)(x
- b)
Die heeft als nulpunten x = a en x = b
dus de as ligt daar midden tussen in bij x = (a
+ b)/2
Wat gebeurt er als we die parabool vermenigvuldigen met de rechte lijn
y = x - c ????
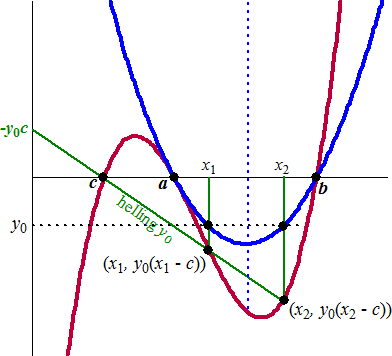
Neem twee punten op gelijke hoogte (y0), dus aan
weerszijden van de as, en noem ze (x1, y0)
en (x2, y0)
Als je die beiden met (x - c) vermenigvuldigt, dan
krijg je de punten (x1, y0 ē (x1
- c)) en (x2, y0 ē (x2
- c)) en die liggen dus op de derdegraadsfunctie. |
| |
|
|
|
|
 |
| |
|
|
|
Als je eens kijkt waar de lijn door die twee punten de x-as
snijdt dan zie je meteen dat dat is bij x = c
Waarom?
Nou, de helling is: |
|
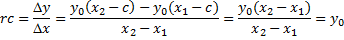 |
De lijn gaat door bijv. (x1,
y0x1 - y0c)
dus dat geeft y0x1 -
y0c = y0 ē x1
+ b ofwel b = -y0c
De lijn snijdt de x-as bij 0 = y0
ē x - y0c dus bij x = c
De eerste eigenschap was dus gewoon een speciaal geval hiervan!
(Het geval x1 = x2 op de as
van de parabool) |
| |
|
|
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |