|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
 |
|
De Sinusregel. |
|
|
| |
|
|
Naamgeving in een driehoek. |
| |
|
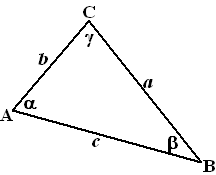
Afspraak:
Voortaan geven we de hoekpunten van een driehoek de namen A, B, C
(hoofdletters)
De hoeken heten
α,
β
en
γ (Griekse letters, en bij hoekpunt A
hoort hoek
α, bij hoekpunt B hoek
β, en bij hoekpunt C hoek
γ)
De zijden heten a, b en c (kleine letters) waarbij
een zijde dezelfde naam heeft als de hoek ertegenover.
't Is allemaal zoals in de figuur hiernaast. |
 |
| |
|
|
Berekeningen. |
|
| |
|
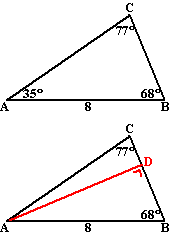
Als we van een driehoek alle
hoeken kennen en één zijde, dan kunnen we in principe de andere zijden
berekenen.
Hiernaast zie je een driehoek ABC met hoeken zoals aangegeven en zijde
AB = 8.
Als je daarin de hoogtelijn AD tekent, dan kun je in driehoek ABD
sos-cas-toa toepassen.
Dat geeft sin68º = AD/8
ofwel AD = 8 • sin68º
Maar die AD kun je nu weer gebruiken voor sos-cas-toa in driehoek ADC.
Dat geeft sin77º = AD/AC ofwel
AC = AD/sin77º
Met de al gevonden AD geeft dat
AC = 8 • sin68º/sin77º
|
 |
| |
|
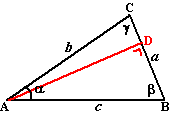 |
Dit was eigenlijk twee keer "SOS".
Maar als we de hoeken
α,
β en
γ
noemen en de zijden a, b en c, dan kunnen
we de berekening hierboven automatiseren:
in driehoek ABD: sinβ =
AD/c dus AD = c
• sinβ
in driehoek ADC: sinγ =
AD/b dus b =
AD/sinγ =
c • sinβ/sinγ
|
| |
|
| Als je nu "voor de mooiheid" sinβ
naar de andere kant doet, dan staat er het prachtig symmetrische
b/sinβ =
c/sinγ. |
|
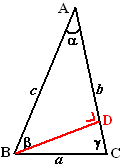 |
En als je de driehoek draait, dan kun je
natuurlijk precies hetzelfde nóg een keer doen!!! Dat zou dan
geven C/sinγ
= A/sinα
Samengevat vinden we de sinusregel:
|
| |
|
Het is de moeite waard deze regel
uit je hoofd te leren. Dan hoef je niet elke keer de afleiding hierboven
weer te verzinnen.
Natuurlijk kun je deze sinusregel ook gebruiken als je een hoek niet
weet, maar wel twee zijden. |
| |
|
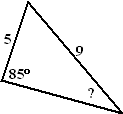
| Voorbeeld 1. Bereken
de hoek met het vraagteken in de driehoek hiernaast.
De sinusregel geeft: 9/sin(85) = 5/sin(?)
Dus: sin(?) = 5 • sin(85)/9
≈ 0,5534
Daaruit volgt ? = sin-1(0,5534)
≈ 33,6º. |
 |
|
| |
|
| De
sinus van een stompe hoek. |
| |
|
De sinusregel geldt ook voor
driehoeken met een stompe hoek, maar er is een kleine complicatie.....
Zolang je de sinusregel gebruikt om lengtes van zijden uit te rekenen is
er geen vuiltje aan de lucht. Maar zodra je probeert een hoek te
berekenen krijg je wel eens een fout antwoord. Dat zit hem allemaal in
die sin-1-functie. |
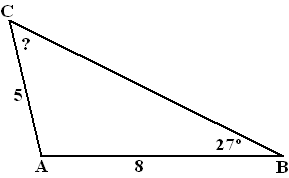
Neem de driehoek hiernaast.
De sinusregel geeft: 5/sin27 = 8/sin?
dus sin? = 8 • sin27/5
≈ 0,726
Dan geldt ? = sin-1(0,726)
≈ 46,6º
Maar dat is niet de enige mogelijkheid!
Met een zijde van 8, een zijde van 5 en een hoek van 27º op de plaatsen
als hiernaast is er nog een tweede mogelijkheid voor de driehoek!
Kijk maar: |
 |
| |
|
|
 |
| |
|
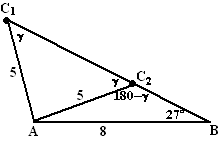
In de linkerfiguur zie je de
voorwaarden: AB = 8 , de hoek bij B is 27º. Vanaf A is een zijde
van 5 getekend.
Punt C ligt dus ergens op de cirkel met A als middelpunt en met straal
5. Een deel daarvan is getekend.
Maar nu zie je meteen dat er voor de plaats van punt C twee
mogelijkheden zijn: C1 en C2.
C1 geeft de oplossing die we hierboven al vonden: een
hoek van 46,6º.
Maar in de figuur helemaal rechts zie je dat er nóg een oplossing is,
deze keer met een stompe hoek bij C!!!
Ook in deze driehoek zou gelden 5/sin27 =
8/sin? . Waarom vinden we die tweede
oplossing dan niet?
Hoe kan dat?
Het zit hem allemaal in de onbetrouwbaarheid van de functie sin-1x.
Die geeft als antwoord altijd een scherpe hoek.
Zo komt er uit sin-1(0,726) een hoek van 46,6º .
Dat is geen fout antwoord, want het klopt wel dat sin(46,6º) =
0,726. |
Maar dit antwoord is niet volledig! Want ook
sin(133,4º) = 0,726. En die tweede hoek wordt zomaar verzwegen door sin-1x.
In de figuur hiernaast zie je dat, als die eerste hoek gelijk is aan
γ, dat dan de tweede verzwegen hoek gelijk is
aan 180º-γ. Dat volgt uit het feit dat
driehoek AC1C2 gelijkbenig is.
Je reinste discriminatie van de stompe hoeken!!!!! |
 |
| De enige oplossing voor dit probleem is, dat
je zelf zodra je die sin-1x gebruikt even
controleert of je wel de goede hoek krijgt of dat je misschien 180º-min-die-hoek
moet doen. |
| |
|
|
Als je sin-1x
gebruikt kan het antwoord ook
"180º-min-het-gevonden-antwoord"
zijn! |
|
| |
|
| |
|
|
|
OPGAVEN |
| |
|
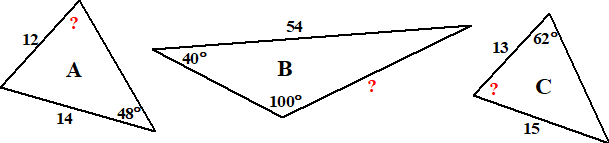
| 1. |
Bereken de grootte van het vraagteken in de
driehoeken hieronder. Geef je antwoorden in één decimaal
nauwkeurig. |
| |
|
| |
 |
| |
|
| |
|
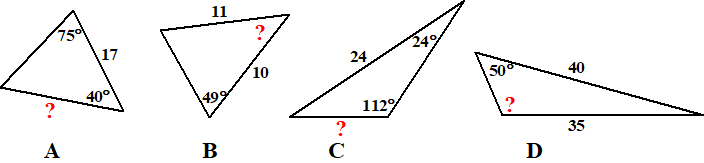
| 2. |
Bereken de grootte van het vraagteken in de
driehoeken hieronder. Geef je antwoorden in één decimaal
nauwkeurig. |
| |
|
|
|
| |
 |
| |
|
|
|
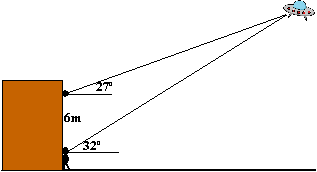
| 3. |
Nee maar! Kleine Karel
ziet 's nachts vanuit zijn slaapkamerraam een vliegende schotel!
Hij pakt natuurlijk direct zijn geo-driehoek en meet een
kijkhoek van 27º ten opzicht van een horizontale lijn.
Dan rent hij naar beneden en meet op een plaats 6 meter lager
een kijkhoek van 32º met een horizontale lijn.
Bereken de horizontale afstand van de schotel tot het huis van
Kleine Karel. |
 |
| |
|
|
|
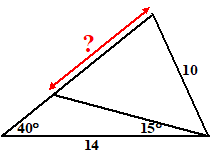
| 4. |
Bereken het vraagteken
in de figuur hiernaast. |
 |
|
|
|
 |
|
|
|
© h.hofstede (h.hofstede@hogeland.nl) |
|