|
© h.hofstede (h.hofstede@hogeland.nl) |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Meer opgaven |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
Geef de coördinaten van de buigpunten van de grafieken van de volgende functies: | |||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | f(x) = x4 + 2x3 - 36x2 + 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | f(x) = 2x√x - 3x2 + 8x | |||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | f(x) = x2 • (1 - √x) | |||||||||||||||||||||||||||||||||||||||||||||||||||
 |
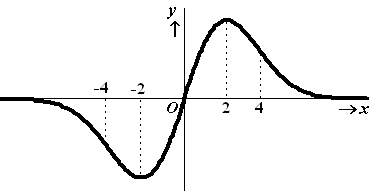
Hieronder staat de grafiek van een functie. De plaats van de nulpunten, de buigpunten en de extremen is aangegeven. | |||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Vul in de onderstaande tabel overal = 0 of < 0 of > 0 in. | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
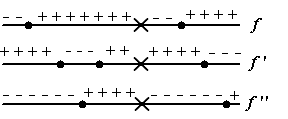
Hieronder
staan van een functie f de tekenbeelden van f , f
' , en van f ''. Schets een mogelijke grafiek van f die daar bij zou kunnen horen. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
Gegeven is de
functie: f(x) = 3x3 +
9x2 + 2x + c Voor welke c valt het buigpunt samen met een nulpunt? |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. | Gegeven zijn de functies fa(x) = x3 - 4x2 + 2x + 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Onderzoek algebraïsch of het buigpunt van de grafiek van f midden tussen beide toppen in ligt. (je mag afronden) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 6. | Gegeven zijn de
functies f(x) = x2 + 64Öx
en g(x) = x3
- 12x2 + 272 Toon aan dat de grafieken van f en g een gemeenschappelijk buigpunt hebben. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7. | Iemand beweert dat van een algemene
derdegraads functie y = ax3 + bx2
+ cx + d de x-coördinaat van het buigpunt altijd midden tussen
de x-coördinaten van beide toppen in ligt. Onderzoek of dat inderdaad het geval is. |
|
| 8. | Gegeven is de functie: | |
|
|
||
| Geef de coördinaten van de buigpunten van de grafiek van f. | ||
| 9. | Gegeven is de functie f(x) = x4 - 4x3 - px2 - 8x - 2 | |
| a. | Geef de coördinaten van de buigpunten van de grafiek f(x) als p = 18 | |
| b. | Waarom heeft de grafiek van f geen buigpunten voor p = -10? | |
| c. | Voor welke p heeft de grafiek van f precies één buigpunt? | |
| 10. | Hieronder zie je in één figuur de
grafieken van f en f ' en f '' Leg duidelijk uit welke grafiek bij welke functie hoort. |
|
|
|
||
| 11. | Hieronder zie je in één figuur de
grafieken van f en f ' en f '' Leg duidelijk uit welke grafiek bij welke functie hoort. |
|
|
|
||
| 12. | Examenvraagstuk VWO Wiskunde
B, 2022-II De functie f is gegeven door f (x) = 2(2x - 1)3 + 3(2x - 1)2 . Voor de afgeleide geldt: f '(x) = 48x2 - 24x |
|
| a. | Bewijs dit. | |
| De lijn k raakt de grafiek van f in het buigpunt. | ||
| b. | Stel door middel van exacte berekeningen een vergelijking op van k. | |
| 13. | Examenvraagstuk VWO Wiskunde
B, 2022-II De vierdegraadsfunctie f wordt gegeven door f(x)= x4 - 30x2 . De grafiek van f heeft twee buigpunten met dezelfde y-coördinaat. De lijn door de buigpunten B en C snijdt de grafiek van f in twee andere punten, A en D. Zie de figuur. |
|
|
|
||
| Bereken exact de lengte van AD. | ||
| © h.hofstede (h.hofstede@hogeland.nl) | ||
 |
||
