© h.hofstede (h.hofstede@hogeland.nl)

Nogmaals de discriminant.
 
We zagen al eerder dat de discriminant van een kwadratische vergelijking bepaalt hoeveel oplossingen er zijn. Nog even heel kort samengevat:

ax2 + bx + c = 0
D = b2 - 4ac
D > 0 :  twee oplossingen
D = 0 :  één oplossing
D < 0 :  geen oplossing
Het wordt wiskundig pas echt interessant als we functies bekijken met een parameter (meestal de letter p) erin.
Neem bijvoorbeeld het volgende:

Probleem
Gegeven zijn de lijn  y = 2x + 3  en de parabool  y = x2 + 4x + p
Voor welke waarde(n) van p hebben deze lijn en deze parabool geen snijpunten?

Oplossing.
We doen gewoon alsof we die vervelende p niet in de gaten hebben en gaan de snijpunten van deze lijn en deze parabool uitrekenen (dat zal dus niet lukken vanwege die p maar dat hebben we even niet door):

x2 + 4x + p = 2x + 3
⇒  x2 + 4x + p - 2x - 3 = 0
⇒  x2 + 2x + p - 3 = 0

Dit is een kwadratische vergelijking met a = 1,  b = 2 en c = p - 3
De oplossingen daarvan zijn de snijpunten van de lijn met de parabool.
De vraag is dus eigenlijk:  "Wanneer heeft deze vergelijking géén oplossingen?"
Nou, dat staat in bovenstaande tabel:  Als D < 0
D = 22 - 4 • 1 • (p - 3) = 4 - 4p + 12 =  16 - 4p
Dat is kleiner dan nul als  p > 4
Kortom: de parabool en de lijn hebben géén snijpunten als  p > 4

Het volgende plaatje demonstreert dat nog eens.

   
RAKEN
Wiskundigen hebben het over twee grafieken die elkaar raken als ze door het zelfde punt gaan, maar daar ook dezelfde helling hebben. Ze liggen als het ware "tegen elkaar aan". In de middelste figuur hierboven is dat het geval.
Voor parabolen en rechte lijnen betekent "raken" niets anders dan  "'één snijpunt hebben", dus het oplossen van het snijpunt zal een vergelijking met D = 0 geven.
   
 
 
OPGAVEN
1. a. Voor welke p heeft de vergelijking  3x2 + 5x + p = 0  precies één oplossing?
     
  b. Voor welke a heeft de vergelijking  ax2 + 4x - 8 = 0  geen oplossingen?
     
  c. Voor welke p heeft de vergelijking  -3x2 + px + 6  twee oplossingen?
     
2. Voor welke waarden van r snijdt de lijn y = 4x - 1  de cirkel  x2 + y2 = r2  in twee punten?
     
3. a. Voor welke p raken de lijn  y = 3x + p  en de parabool  y =  5x - x2  elkaar?
     
b. Voor welke p raken de parabolen  y = 3x2 + 4x + p  en  y = -x2 + 5x + 4  elkaar?
     
c. Voor welke p raken de parabool  y = 5x2 + px + 12 en de lijn  y = x + 5 elkaar?
   
4. Als iemand een projectiel weggooit onder een hoek van 45º met een snelheid v, dan beschrijft dat projectiel een paraboolbaan waarvoor ongeveer geldt: y = vx - (9,8/v²) • x2
Iemand staat onder een schuine  afkapping en wil een bal weggooien. De afmetingen staan in de figuur hiernaast.
Hij gooit de bal weg vanaf punt O dat we als oorsprong kiezen.

     
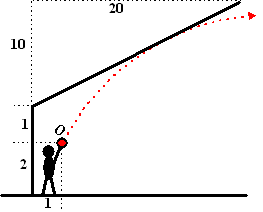
a. Toon aan dat bij deze keuze van O  de vergelijking van het schuine dak   y = 1,5 + 0,5x  is
     
  b. Met welke snelheden kan de man de bal weggooien zodat hij niet tegen het schuine dak komt? Rond je antwoord af op twee decimalen. Ga ervan uit dat de bal zelf geen afmetingen heeft.
   

© h.hofstede (h.hofstede@hogeland.nl)