| |
© h.hofstede (h.hofstede@hogeland.nl)
|
| Lineair verband |
 |
|
| |
|
|
|
Karel gaat elke vrijdagavond naar de kroeg en
drinkt daar altijd alleen maar bier. Gewoon omdat hij dat lekker
vindt.
Een glas bier kost er €1,70.
Karel onderzoekt het verband tussen het aantal glazen bier (G) dat hij
drinkt en het bedrag (B) dat hij kwijt is.
Dat levert hem de volgende tabel:
| |
| Glazen G |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| Bedrag B |
1,70 |
3,40 |
5,10 |
6,80 |
8,50 |
9,20 |
10,90 |
12,60 |
|
| |
Het valt op dat de getallen in de onderste rij steeds
met dezelfde hoeveelheid toenemen. Dat is logisch natuurlijk want dat is
uiteraard precies de prijs van een glas.
Zo'n verband tussen G en B waarbij de toename elke keer hetzelfde is
heet een lineair verband.
|
| |
|
Dat woord komt van
linea en dat betekent rechte
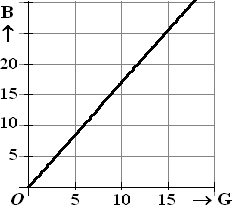
lijn. Ik hoop dat je het logisch vindt dat de grafiek van zo'n lineair
verband een rechte lijn is, immers bij elk stapje van één naar rechts
(G één groter) neemt de hoogte B met dezelfde hoeveelheid
toe.
(eigenlijk zijn het in de grafiek hiernaast natuurlijk losse stippen, want het
aantal glazen moet een geheel getal zijn, maar voor het gemak is een
doorgetrokken lijn getekend).
Karel stelt een formule op voor het bedrag (B) dat hij op een avond
kwijt is als functie van het aantal glazen bier (G) dat hij naar binnen
heeft gewerkt. De formule voor deze lijn kun je natuurlijk
makkelijk zelf
verzinnen. Doe dat maar. Hij staat hieronder.
|
 |
| |
|
Maar eens in de maand is er in de kroeg
live-muziek. Om dat te kunnen betalen vraagt men dan een
entreeprijs van €7,00.
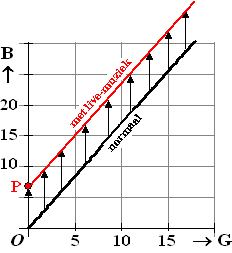
Karel merkt natuurlijk dat het bedrag dat hij dan kwijt is steeds
€7,00 hoger ligt dan op de avonden zonder live-muziek. In zijn grafiek
betekent dat, dat elk punt 7,00 omhoog gaat.
Dat geeft de nieuwe rode grafiek hiernaast.
De lengte van alle pijltjes is dus 7,00.
Merk op dat de rode lijn even steil loopt als de oorspronkelijke, dus
hetzelfde hellinggetal zal hebben. De lijn gaat echter niet meer door de
oorsprong, maar is verschoven naar punt P(0, 7)
Wat betekent dat voor de formule?
Nou, als elke B 7,00 groter wordt kun je zeggen: "Nieuwe
formule is oude formule plus 7,00" ofwel: |
 |
| |
|
|
| |
|
|
|
|
Wat kunnen we uit dit
alles concluderen? |
| |
|
|
|
| De formule van een willekeurige
rechte lijn ziet er altijd uit als y = ax + b waarbij a
het hellinggetal is, en b het snijpunt met de y-as (dat
punt P (0,7) van het vorige voorbeeld, weet je nog?). |
| |
|
|
| |
|
|
|
| |
|
|
|
Nou je dit eenmaal weet kun je
een rechte lijn waarvan de formule gegeven is natuurlijk makkelijk
binnen 5 seconden tekenen. TOCH???
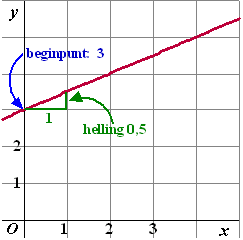
Stel dat je bijvoorbeeld de lijn y = 0,5x + 3 moet
tekenen.
Nou dan begin je bij 3 op de y-as en gaat dan steeds 1 opzij en
0,5 omhoog.
Binnen 5 seconden heb je de lijn hiernaast!
PAS OP!!
Kijk wel even goed uit welk getal a is en welk b. Het is
niet zo dat a altijd het eerste getal is en b het tweede.
Soms is je leraar in een melige bui en zet hij de formule expres
verkeerd om neer! Ikzelf zou zoiets natuurlijk als leraar NOOIT
doen, maar ja, ik ken jouw leraar niet.... misschien is het wel een
eikel....
Zo kun je de formule y = 0,5x + 3 natuurlijk net zo goed
schrijven als
y = 3 + 0,5x. Flauw hé? |
 |
| |
TRAP DAAR NIET
IN:
Blijf vooral cool en relaxed en kijk gewoon steeds
welk getal bij x staat:dat is het hellinggetal a,
en b is altijd het "losse" getal dat alleen staat. |
| |
|
|
|
|
a
staat bij x
b staat alleen |
|
| |
|
|
|
|
Stressoefening 1:
Pak een papier en teken alvast een assenstelsel waarbij x
en y beiden van -10 tot en met 10 lopen.
Als je op de knop hieronder clickt, dan krijg je een aantal
vergelijkingen van rechte lijnen. Probeer er zoveel mogelijk van
te tekenen voordat de laadbalk is volgelopen. |
| |
|
|
|
|
| |
 |
| |
|
Stressoefening 2:
Hieronder verschijnen steeds grafieken van rechte lijnen, met
ernaast 4 mogelijke formules.
't Is multiple-choice:
Noteer steeds welke formule (a, b, c of
d) volgens jou bij de getekende lijn hoort.
pas op: de lijnen verschijnen steeds sneller
en zijn dus steeds korter te zien. ik ben benieuwd hoe ver je
komt......
pas extra op: oeps, ik ben tóch een eikel... |
| |
|
|
|
|
| |
 |
| |
|
|
|
| |
|
|
|
OPGAVEN |
| |
|
|
|
|
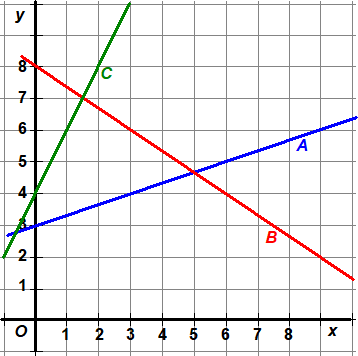
| 1. |
Stel een vergelijking
op van de volgende rechte lijnen: |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| 2. |
Recent onderzoek
heeft uitgewezen dat de gemiddelde temperatuur van de aarde langzaam
stijgt. Een aantal wetenschappers heeft het lineaire model T =
0,02t + 8,50 voorgesteld, waarbij t de tijd in jaren is
vanaf 1900
(dus t = 0 in 1900), en T de gemiddelde temperatuur in
graden Celsius. |
| |
|
|
|
|
| |
a. |
Wat stelt het getal 8,50 in de
praktijk voor? |
| |
|
|
|
|
| |
b. |
Wat stelt het getal 0,02 in de
praktijk voor? |
| |
|
|
|
|
| |
c. |
In 2014 was de gemiddelde
temperatuur 10,6 ºC
Hoeveel hoger of lager is dit dan het model voorspelde? |
| |
|
|
|
|
| |
d. |
Wanneer zal
de gemiddelde temperatuur volgens dit model gelijk zijn aan 11,5
ºC ? |
| |
|
|
|
|
| 3. |
Gerard speelt al jarenlang bij de golfclub.
Het basislidmaatschap is per jaar €185,- maar daarnaast moet hij
elke keer dat hij de baan gebruikt ook nog €5,- speelgeld betalen.
Daarnaast is hij nog meer geld kwijt. Een golfbal kost €1,50 en die
raakt hij regelmatig kwijt omdat hij ze de bosjes of het water in
slaat. Per twee keer spelen is hij wel een bal kwijt.
Stel een formule op voor het geld dat Gerard per jaar kwijt is als
functie van het aantal keer dat hij heeft gespeeld. |
| |
|
|
|
|
| 4. |
Een
werknemer wil in verband met zijn nieuwe baan gaan verhuizen van
Groningen naar Maastricht. Daarvoor zoekt hij een verhuisbedrijf. Hij
heeft berekend dat alles wel in één verhuiswagen kan, en leest de
offertes van twee verhuisbedrijven. Het betreft de bedrijven Budget
Verhuisservice, Mast BV.
Elk bedrijf vraagt voor het gebruik van een verhuiswagen een vast bedrag
per dag. Verder komt daar nog bovenop een bedrag per kilometer.
Budget Verhuisservice vraagt voor de wagen €400,- en verder per km nog
€2,50.
Mast BV vraagt voor de wagen €550,- en verder per km nog €1,60. |
| |
|
|
|
|
| |
a. |
Stel formules op voor
de totale vervoerkosten K als functie van de afstand a |
| |
|
|
|
|
| |
b. |
Schets de
grafieken voor beide verhuisbedrijven en lees af bij welk aantal
kilometers bedrijf Mast BV de goedkoopste is. |
| |
|
|
|
|
| 5. |
We hebben een heleboel
lijnen die er uitzien als y = ax + 4
- 3a
Daarbij is a een willekeurig getal.
Wat hebben al deze lijnen met elkaar gemeenschappelijk?
Onderzoek dat door er een aantal te tekenen.
Kun je deze eigenschap ook met de formule verklaren? |
| |
|
|
|
|
| |
|
|
|
|
 |
|
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|