De lengte van een grafiek.

© h.hofstede (h.hofstede@hogeland.nl)
Stel dat we de lengte van de grafiek van y = x2  tussen x = -2 en x = 2 willen berekenen zoals getekend in de figuur hiernaast.

Om die te berekenen snijden we hem in allemaal kleine stukjes met lengte ds.  Eén zo'n stukje ds is hiernaast getekend en staat naast de figuur uitvergroot.

De lengte van dat ene stukje kunnen we uitrekenen met Pythagoras: ds2 = dx2 + dy2   dus  ds = √(dx2 + dy2)  
Om de totale lengte nu uit te rekenen stellen we een integraal op overal die stukjes ds:

Het probleem is echter dat de grenzen van de integraal x-grenzen zijn, maar dat er ook nog dy in staat, en bovendien dat dx en dy onder een wortelteken staan. Dat valt zo niet uit te rekenen.
Gelukkig is er een goede en slimme truc om al die problemen in één keer te verhelpen:
In de laatste stap is gebruikt dat  dy/dx gelijk is aan de afgeleide functie f '.
Die afgeleide is in dit geval gelijk aan 2x, dus:

Maar deze is te moeilijk om te primitiveren. Daarom benaderen we hem met de GR.
Y1 = √(1 + 4x2 ) en dan calc - integraal  geeft als benadering   L ≈ 9,29 

Algemene formule:

  

En nu het goede nieuws   

Deze integraal kun je eigenlijk nooit algebraïsch berekenen, dat is gewoon te moeilijk. ((om precies te zijn komt er in het bovenstaande voorbeeld uit:   2√17 + 1/4ln(2√68 + 16) - 1/4ln(2√68 - 16)   WAUW!!)
Veel te moeilijk dus....
Het mag allemaal met de GR benaderd worden.

   
 OPGAVEN
1. Bereken in twee decimalen nauwkeurig de lengte van de grafiek van y = ln(x + 1)  tussen x = 0 en  x = 2

2,30
   
2. V is het vlakdeel ingesloten door de grafieken van f(x) = √x  en  g(x) = x2
Benader de omtrek van V in twee decimalen nauwkeurig.
         

2,96
3. Als je van de grafiek van f(x) = sinx de periode halveert, dan zul je tussen 0 en 2π twee periodes hebben in plaats van één.  Onderzoek of de lengte van de grafiek tussen 0 en 2π daardoor ook is verdubbeld.
         

1,38 keer
           
4. Iemand beklimt een heuvel waarvan het vooraanzicht hoort bij de vergelijking  h(x) = 0,24x - 0,00003x2 

De heuvel is bij de top horizontaal.

Hoeveel procent van de weg heeft hij afgelegd als hij op de helft van de hoogte van de top is?

         

29,6%
5. Er is één functie waarvan je deze integraal wél algebraïsch kunt berekenen, en dat is f(x) = x√x
De grafiek van f(x) = x√x  tussen x = 0 en x = a  heeft lengte 64/27. Bereken algebraïsch  a.
 

a = 4/3
     
6. Gegeven zijn de functies  f(x) = 10 - x2  en  g(x) = x2 - 8x
De grafieken van deze twee functies sluiten samen een vlakdeel V in.
     
  a. Bereken algebraïsch de oppervlakte van V.
         
  b. Bereken de omtrek van V.
         
7. Een kabel hangt tussen twee lange verticale palen die 60 meter uit elkaar staan.
Bij deze kabel hoort de formule  y = 6·(e0,05x + e-0,05x)
         
  a. Op welke hoogte is de kabel aan de palen bevestigd?
       

28,23 m
  b. Bereken de lengte van de kabel.
       

70,73 m
         
8. Examenvraagstuk VWO Wiskunde B, 2003

Gegeven is de functie:  f(x) = x  + 4/x
V is het gebied dat wordt ingesloten door de lijn y = 5 en de grafiek van f.
         
  a. Bereken met behulp van primitiveren de exacte waarde van de oppervlakte van V.
       

4,5 - 8ln2
  b. Bereken de omtrek van V in twee decimalen nauwkeurig.
       

6,79
         
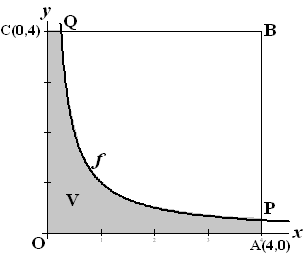
9. Examenvraagstuk VWO Wiskunde B, 2006

Van een vierkant OABC met zijde 4 ligt A op de positieve x-as en C op de positieve y-as.
Verder is gegeven de functie  f(x) = 1/x
De grafiek van f verdeelt het vierkant in twee stukken. Eén van die stukken is in onderstaande figuur grijs gekleurd; dat stuk noemen we V.

       
  a. Bereken de omtrek  van V in twee decimalen nauwkeurig.
     

14,80
  b. Toon aan dat de oppervlakte van V exact gelijk is aan  1 + 2ln4
         
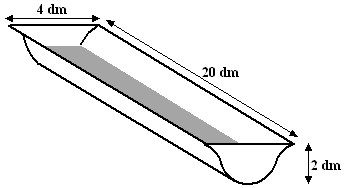
10. Examenvraagstuk VWO Wiskunde B, 2006.

In de figuur hiernaast staat een tekening van een drinkbak voor dieren. De bak bestaat uit drie delen: een rechthoekige metalen plaat die gebogen is tot een symmetrische goot, een voorkant en een achterkant die aan de goot gelast zijn.
De bak is 20 dm lang, 4 dm breed en 2 dm diep.
De gebogen vorm van de goot is de grafiek van de functie:
 f(x) = -1/8x4  + x3 - 2x2 + 2 
(x en y in dm, en 0 ≤ x ≤ 4)
         
  a. Bereken in liters nauwkeurig hoeveel water de bak bevat als hij tot de rand gevuld is.
       

851/3
  b. Bereken in dm2 nauwkeurig de oppervlakte van de rechthoekige plaat waarvan het gebogen deel van de drinkbak gemaakt is.
       

117
         
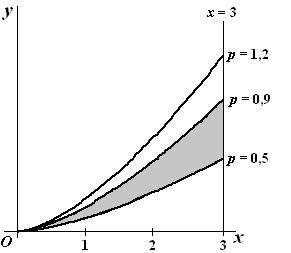
11. Examenvraagstuk VWO Wiskunde B, 2007.
         
  Voor elke p > 0 is de functie f p gedefinieerd door fp(x) = p • x1,5 met domein [0, 3]. In onderstaande figuur is de grafiek van f p getekend voor p = 0,5 , voor p = 0,9 en voor p = 1,2 .

Het vlakdeel G , ingesloten door de grafiek van f0,5 , de grafiek van f0,9 en de lijn x = 3, is in deze figuur met grijs aangegeven.

       
  a. Bereken de oppervlakte van G in twee decimalen nauwkeurig.
       

2,49
  b. L(p) is de lengte van de grafiek van fp. Bereken  L(2/3) exact.
       

42/3
   

© h.hofstede (h.hofstede@hogeland.nl)