| |
 |
|
Laplace-transformaties. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
Weet je nog, vroeger, toen je nog
maar net met wiskunde was begonnen? Toen het leven nog simpel was??
Toen kreeg je bijvoorbeeld de balans-methode.
Dat werkte als volgt: je had een vergelijking die je moest
oplossen, bijvoorbeeld 2x + 4 = 10
En dan ging je aan beide kanten van het "=" teken hetzelfde doen, om de
vergelijking eenvoudiger te maken.
In dit geval deed je waarschijnlijk eerst beide kanten "-4" want
dan hield je over 2x = 6
En daarna deed je beide kanten "/2" want dat gaf x =
3. |
| |
|
|
|
|
als je beide kanten van een
vergelijking hetzelfde doet, dan blijft het kloppen. |
|
| |
|
|
|
| Een
differentiaalvergelijking is natuurlijk ook een vergelijking.... Dus daar mag je ook best beide kanten hetzelfde doen.
Nou is een Laplace-transformatie "iets" dat je aan beide kanten
van een differentiaalvergelijking kunt doen waardoor al die vervelende
afgeleides eruit wegvallen! Een Laplace-transformatie laat alle
y'''' en y'' en y'' en zo
verdwijnen en maakt er gewone y van.
Daardoor wordt een differentiaalvergelijking omgezet in een
algebra-probleem. En dat is (vaak) makkelijker op te lossen. |
| |
|
|
|
|
Wat gaan we aan beide kanten doen om
die vervelende afgeleides kwijt te raken? |
| |
|
|
|
| Oké, daar komt íe: |
| |
|
|
|
|
|
| |
|
|
|
Die f(t) is dus de
hele linkerkant of de hele rechterkant van een
differentiaalvergelijking.
Let goed op: aan de rechterkant wordt er een integraal over t
uitgerekend. Dat betekent dat die kant geen functie van t meer
is. De integraal is een functie van s. Bij een
Laplace-transformatie stap je over van de variabele t naar de
variabele s. |
| |
|
|
|
|
Waaróm verdwijnen die afgeleides? |
| |
|
|
|
Laten we L(y' ) berekenen,
dan zien we dat vanzelf.
Met partieel primitiveren vind je het volgende: |
| |
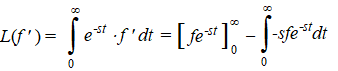 |
| Aan de rechterkant
staan nu twee stukken |
| • |
In het eerste stuk
aan de rechterkant kun je voor t de grenzen invullen.
Dat geeft f(∞)
∙ e-s∙∞
- f(0)
∙ e-s∙0 = f(∞)
∙0
- f(0)
∙ 1 = -
f (0)
(dat gaat er wel van uit dat voor de functie f bij oneindig
geldt, dat f/ex
naar nul gaat) |
| • |
Het tweede stuk is de
Laplace transformatie van f : s • L(f ) |
|
Samen geeft dat: |
|
L(f ') =
s · L(f )
-
f(0) |
|
| |
|
|
|
En als je hierin overal
f vervangt door f ' dan krijg je:
L(f '' ) = s • L(f ' ) - f ' (0) = s
• (s • L(f) - f(0)) - f ' (0) = s2
• L(f) - s • f(0) - f ' (0) |
| |
|
|
|
|
L(f
'' ) = s2
· L(f ) -
s · f(0) - f '(0) |
|
| |
|
|
|
| Bovendien geldt voor Laplace
transformaties de volgende handige eigenschap: |
| |
|
|
|
|
L(a • f + b • g)
= a • L(f ) + b • L(g) |
|
| |
|
|
|
Dat volgt erg eenvoudig direct
uit de eigenschappen van integralen. Bewijs het zelf maar als je er
echt dringende behoefte aan hebt......
Met deze laatste drie eigenschappen kunnen we nu elke tweede orde
differentiaalvergelijking omzetten naar een "gewone" vergelijking. |
| |
|
|
|
| Voorbeeld
1. |
|
Gegeven is de
differentiaalvergelijking: y'' - 3y'' +
2y = 4x met y(0) = 2 en y'(0) =
1
Maak van deze vergelijking een "gewone" vergelijking
Eest neem je (á la balansmethode) van beide kanten van de vergelijking
de Laplace transformatie:
L(y'' - 3y'' + 2y) = L(4x)
⇒ L(y'' ) - 3L(y' ) + 2L(y) = L(4x)
⇒ s2L(y) -
sy(0) - y' (0) - 3(sL(y) - y(0)) + 2L(y)
= L(4x)
⇒ L(y) • (s2 -
3s + 2) - (2s + 5) = L(4x)
.....(1)
Eerst maar eens die Laplace-transformatie van 4x uitrekenen.
Partieel primitiveren geeft: |
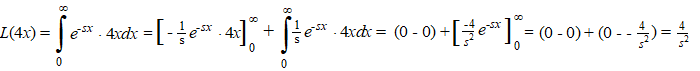 |
| Daarmee wordt
vergelijking (1): L(y) • (s2 - 3s
+ 2) - (2s + 5) = 4/s2 |
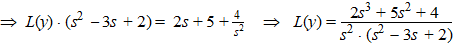 |
Daarmee zijn alle
afgeleides verdwenen, en is dit een algebraïsche functie voor L(y)
geworden.
Maar omdat we natuurlijk een functie voor y zélf willen hebben
zullen we nog een manier moeten vinden om een "terug-transformatie" toe
te passen. Een soort omgekeerde Laplace-transformatie die van een
vergelijking met L(y) en s ons weer terugbrengt in de
gewone wereld van y en x
En verder is het ook nog maar de vraag of we altijd zomaar die
Laplace-transformatie van het deel met de x-en (zoals hier
4x) kunnen uitrekenen.
Dat lijkt me een mooi project voor de volgende twee lessen:
• Volgende les: hoe maak ik
Laplace-transfomaties?
• Les daarna: hoe maak ik inverse
Laplace-transformatie?
Daarna komen we wel weer terug op de differentiaalvergelijkingen. |
| |
|
|
|
| |
|
|
|
|
| 1. |
Maak van de volgende differentiaalvergelijkingen
een "normale" vergelijking voor de Laplace-getransformeerde
functie L(y) |
| |
|
|
|
|
| |
a. |
y'' + 8y = 5 met
y(0) = 3 en y'(0) = 3 |
| |
|
|
|
|
| |
b. |
y'' - 2y' + y
= ex met y(0) = -1 en
y' (0) = 1 (neem aan dat s
> 1) |
| |
|
|
|
|
| |
c. |
y'' + 5y' +
6y = x met y(0) =
y' (0) = 2 |
| |
|
|
|
|
| 2. |
a. |
Stel een formule op voor de
Laplace-transformatie van de derde afgeleide f ''' van een
functie f . In je formule mogen (uiteraard) geen
afgeleides meer voorkomen |
| |
|
|
|
|
| |
b. |
Kun je een algemene formule
opstellen voor de Laplace-transformatie van de nde
afgeleide f (n) van een functie f? |
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|