| |
 |
| |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| Kwadraatformules
uit verhaaltjes... |
|
|
Er zijn een paar
"soorten" verhaaltjessommen waar kwadraten in voorkomen.
Hier volgen van die soorten een voorbeeld. |
|
|
| soort 1: omzet |
|
|
In veel economische modellen
blijkt dat het aantal verkochte producten afhangt van de prijs per
product.
Als de prijs ergens van hoger wordt, dan wordt het aantal verkochte
producten lager.
Voor de omzet (dat is de totale hoeveelheid geld die er binnenkomt)
geldt O = prijs verkochte aantal
Als dat verkochte aantal nou lineair van de prijs afhangt dan krijg
je voor de omzet een kwadratische formule.
Kijk maar: |
|
|
|
voorbeeld
Een marktkoopman merkt dat hij meer sinaasappelen gaat verkopen als hij
de prijs ervan verlaagt. Op dit moment verkoopt hij per dag 120 kg
sinaasappelen voor een prijs van 2,30 per kilo. Hij heeft ontdekt dat
bij elke 10 cent prijsverlaging hij 15 kg extra verkoopt. Stel een
formule voor zijn omzet als functie van de prijs op.
Stel dat hij x keer 10 cent van de prijs afhaalt. Dan wordt zijn
nieuwe prijs in centen p = 230 - 10x.
Het aantal kg dat hij verkoopt is gelijk aan 120 + 15x
Zijn omzet is dus
(230 - 10x)(120 + 15x) = -150x2
+ 2250x + 27600
en dat is een kwadratische functie.
De maximale omzet vinden we bij de top van deze parabool en die ligt
bij p = 7,5. Hij moet daarvoor dus een prijs van 230 - 10 7,5 = 155 cent per kilo
vragen. |
|
|
| soort 2: Oppervlakte |
|
|
|
Als bij een grotere lengte een kleinere
breedte hoort, dan zal de oppervlakte van een figuur vaak een
kwadratische functie zijn.
voorbeeld
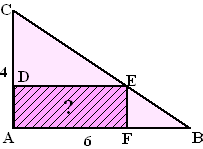
Hiernaast staat een rechthoekige driehoek ABC met rechthoekszijden 4 en
6 getekend met daarin een rechthoek. De vraag is: Wat is de
maximale oppervlakte van deze rechthoek?
|
|
|
|
|
|
Als A de oorsprong is, dan is CB
de lijn y = 4 - 2/3x
Dus als F ligt bij x = p dan is de hoogte EF = 4 - 2/3p
De oppervlakte is dan AF FE = p (4 - 2/3p)
= 4p - 2/3p2
Dat is een parabool met de top bij p = 3 en dan is de
oppervlakte gelijk aan 4 3 - 2/3 32
= 6 |
|
|
|
|
voorbeeld
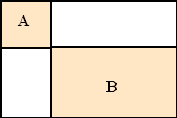
In een rechthoek van 6 bij 4 wordt in de hoek een vierkant A getekend.
Daardoor ontstaat automatisch een rechthoek B.
Hoe groot moet dat vierkant worden als de oppervlakte van A en B
samen gelijk is aan 13,5?
Stel dat A x bij x is, dan is B (6 - x)(4
- x)
Samen is dat x2 + (6 - x)(4 - x) =
x2 + 24 - 10x + x2
= 2x2 - 10x + 24
Dat moet gelijk zijn aan 13,5: |
|
|
2x2 - 10x + 24 =
13,5 geeft 2x2 - 10x + 10,5 =
0
Dat geeft x = 3,5 of x = 1,5
|
| |
|
|
OPGAVEN |
|
|
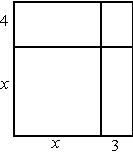
| 1. |
Bereken x in de figuur hiernaast als de
totale oppervlakte gelijk is aan 72 |
|
| |
|
|
| |
|
|
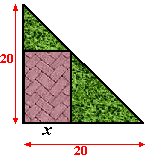
| 2. |
Een grasveld heeft de vorm van een rechthoekige
driehoek met twee zijden van 20.
Er wordt een rechthoekig terras op aangelegd met breedte x.
Bereken x als de oppervlakte van het terras gelijk is aan
96. |
|
| |
|
|
|
|
|
| 3. |
Een vishandelaar verkoopt
in zijn kraam gebakken kibbeling voor 2,95 per portie. Hij
verkoopt bij deze prijs 120 porties per dag, maar een beetje
experimenteren met de prijzen leert hem dat hij voor elke 5 cent
prijsverlaging 8 porties extra verkoopt.
Voor zijn omzet aan kibbeling op een dag geldt dan O(p)
= -1,6p2 + 592p
Daarin is p de prijs per portie in centen en O zijn
omzet in centen. |
| |
|
|
|
a. |
Toon aan dat deze formule
juist is. |
| |
|
|
|
b. |
Bereken bij welke prijs
de man een maximale omzet haalt, en hoe groot deze maximale
omzet is. |
|
|
|
|
|
De man heeft echter ook
onkosten, en die zijn per portie kibbeling gelijk aan
1,40 |
|
|
|
|
|
c. |
Stel een formule op voor
de winst aan kibbeling op een dag, en bereken bij welke prijs de
man de meeste winst maakt. |
| |
|
|
|
|
|
| 4. |
In een tuin van 8 bij 6 meter worden
paden aangelegd die overal even breed zijn. De breedte van de
paden wordt zó gekozen dat de oppervlakten van de paden en van
het overgebleven gras even groot zijn.
Hiernaast zie je twee mogelijkheden om de paden aan te leggen.
Noem de breedte van de paden x
en bereken in beide gevallen hoe groot deze x moet
zijn. |
 |
| |
|
|
|
|
|
|
|
| 5. |
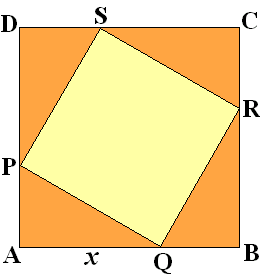
Vierkant ABCD heeft zijden van 5 cm.
Binnen dit vierkant is een kleiner vierkant PQRS getekend.
Hierbij is AQ = BR = CS = DP = x cm.
Voor welke x is de oppervlakte van PQRS 17 cm2 ? |
|
| |
|
|
|
|
|
|
|
| 6. |
Het aantal leden van voetbalvereniging
GVAV is de laatste jaren erg gestegen.
In 2000 was het aantal leden 320, maar vanaf 2000 nam het aantal
leden elk jaar toe met 12.
De contributie was in 2000 gelijk aan 130,- maar die
heeft men sindsdien elk jaar met 4,- verhoogd. |
| |
|
|
|
a. |
Maak een formule voor de totale
hoeveelheid contributie die de penningmeester in een jaar
binnenkrijgt als functie van het jaar (neem t = 0 in
2000) |
| |
|
|
|
b. |
Als dit zo doorgaat, in welk jaar zal
de totale contributie van alle leden dan voor het eerst meer dan
100000 zijn? |
| |
|
|
|
|
|
|
|
| 7. |
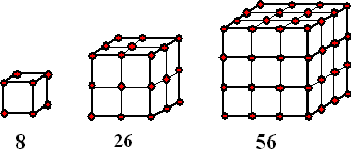
In de onderstaande figuren zijn
roosterpunten op het oppervlakte van een kubus getekend. De
ribben van de kubussen zijn achtereenvolgens 1, 2, 3, ... |
|
|
|
|
|
|
|
|
|
|
|
Voor een kubus met ribbe n is
het aantal stippen gelijk aan A = 6n2 + 2 |
|
|
|
| a. |
Toon aan dat deze formule juist is. |
| |
|
| b. |
Bij de hoeveelste kubus zullen er voor het
eerst meer dan 1 miljoen stippen zijn? |
| |
|
| c. |
Bij de hoeveelste kubus is de
toename van het aantal stippen vergeleken met de
vorige kubus meer dan 1000? |
| |
|
|
|
|
|
| 8. |
Een busmaatschappij organiseert
een groepsreis naar Spanje. Ze vragen per passagier 320,- en
merken dat zich 30 passagiers aanmelden.
Dat vind men een beetje weinig (daarmee is de bus lang niet vol) en
daarom besluit men tot de volgende slimme reclameactie.
Voor elke passagier die zich extra aanmeldt wordt de prijs per persoon
5,- lager! Zo hoopt men dat passagiers ook vrienden en bekenden
zullen aanmoedigen mee te gaan.
Bij welk totaal aantal passagiers zijn de opbrengsten voor de
busmaatschappij maximaal? |
|
|
|
|
| 9. |
Van een vierkant wordt de breedte
6 kleiner gemaakt en de lengte 3 groter. Dan ontstaat een rechthoek met
oppervlakte 70.
Hoe groot was het vierkant? |
| |
|
| |
 |
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|