|
|||||
| Kletterdriehoeken. | |||||
| Eerst maar even wat dat voorstelt: | |||||
|
|||||
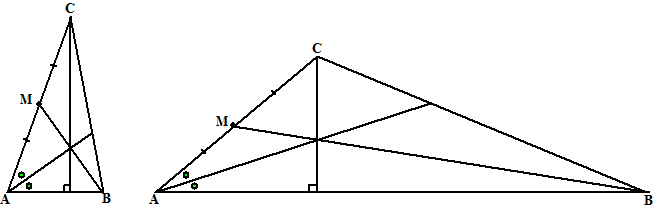
| Hier zie je er twee: | |||||
|
|
|||||
| Tekenen is natuurlijk
een makkie: teken lijnstuk AC en een halve lijn vanaf A (later AB) teken de bissectrice van hoek A. teken de hoogtelijn vanuit C loodrecht op die halve lijn teken de lijn door het midden van M die ook door het snijpunt van de hoogtelijn en de bissectrice gaat waar die lijn de halve lijn vanuit A snijdt ligt punt B. Als je ook de buitenbissectrice van hoek A toelaat kun je stomphoekige Kletterdriehoeken krijgen. Hier zie je wat je krijgt als je in bovenstaande twee voorbeelden de buitenbissectrice neemt: |
|||||
|
|
|||||
| Waarom trouwens deze vreemde naam? | |||||
| Op jacht naar een formule. | |||||
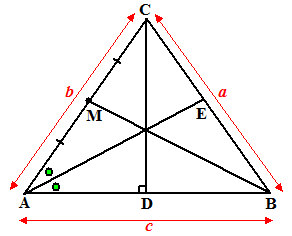
| Neem de
Kletterdriehoek hiernaast. De stelling van Ceva zegt: AD/DB BE/EC CM/MA = 1 Maar omdat M het midden van AC is kun je die laatste wel weglaten: Dat geeft: AD/DB BE/EC = 1 De bissectricestelling (opgave 2 in deze les) zegt: BE/EC = c/b samen met DB = c - AD geeft dat: AD/(c - AD) c/b = 1 ⇒ AD c = b(c - AD) ⇒ AD c = bc - b AD ⇒ AD(b + c) = bc ⇒ AD = bc/(b + c) ............(1) en dus DB = c - bc/(b + c) = c²/(b + c) ...........(2) |
 |
||||
|
Een vereenvoudiging. Laten we een oorsprong (altijd handig bij berekeningen) in A leggen, de x-as langs AB, dan is punt B het punt (c, 0). Dat geeft dan uiteindelijk het mooie resultaat: AD = ½c(2 - c) en DB = ½c2 ........(3) |
|||||
|
Tijd voor Pythagoras. in driehoek ADC: AD2 + CD2 = AC2 dus (met (3)) CD2 = AC2 - AD2 = (2 - c)2 - ¼c2(2 - c)2 in driehoek DBC: BC2 = CD2 + DB2 = (met het vorige resultaat en (3)) = (2 - c)2 - ¼c2(2 - c)2 + ¼c4 = a2 a2 = 4 - 4c + c2 - ¼c2(4 - 4c + c2) + ¼c4 a2 = 4 - 4c + c2 - c2 + c3 - ¼c4 + ¼c4 a2 = 4 - 4c + c3 a = √(c3 - 4c + 4) |
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||