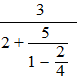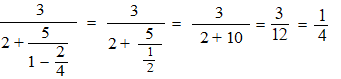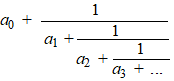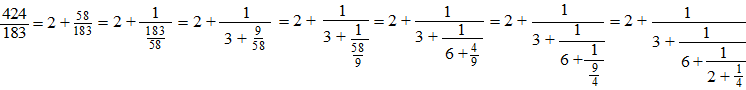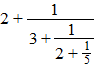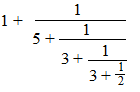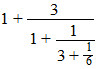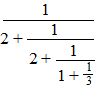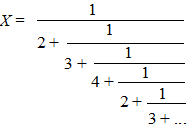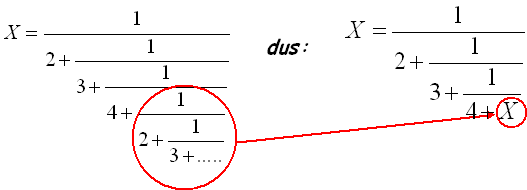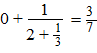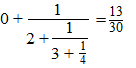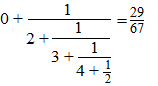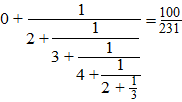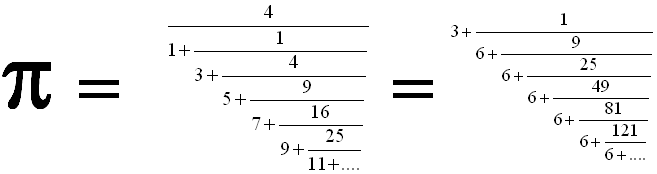kettingbreuken


Kettingbreuken.	© h.hofstede (h.hofstede@hogeland.nl)

delen door een breuk.

euclidisch algoritme

Een kettingbreuk is eigenlijk niets anders dan een breuk in een breuk.

Nou ja, om eerlijk te zijn, meestal is het een breuk in een breuk in een breuk in een breuk in een......enz.
Hier heb je d'r eentje:

Natuurlijk kun je hier ook een "gewone" breuk van maken.
Dat doe je door "van onderaf " alles uit te rekenen. Bedenk daarbij dat delen door breuk gelijk is aan vermenigvuldigen met het omgekeerde (zie anders de voorkennis-les) .
Kijk maar hoe het werkt:

Kennelijk was deze `rare` breuk niets anders dan gewoon ¹/₄ .
Zo kun je elke kettingbreuk omwerken tot een gewone breuk.

1. Basis-Kettingbreuken.

Dat zijn kettingbreuken waarbij alle tellers (die bovenste dingen weet je nog?) gelijk aan 1 zijn.
Dus die zien er zó uit:

In zo'n geval heten die getallen a_1,a_2,a₃ ... ook wel de wijzergetallen van de breuk.
Zo'n breuk wordt verkort genoteerd als {a₀ ; a₁, a₂ , a₃ , ....}

Nou is het leuke dat je elke gewone breuk ook als basis-kettingbreuk kunt schrijven! ECHT WAAR!
Een voorbeeld zal dat denk ik wel duidelijk maken. Het gaat zó:

Zie je het systeem? Elke keer als de teller kleiner is dan de noemer zet je de breuk op z'n kop. Elke keer dat de teller groter is dan de noemer haal je de gehelen er uit.
Hierboven zag je dat de breuk ⁴²⁴/₁₈₃ te schrijven is als {2 ; 3, 6, 2, 4}

Maar wacht eens even.....
Er schiet mij nu iets te binnen...

Als je elke kettingbreuk als gewone breuk kunt schrijven...... (dat zagen we boven aan deze les)

En je kunt elke breuk als basis-kettingbreuk schrijven..... (dat zagen we net)

Dan..................................Dan..............................

Dan kun je elke kettingbreuk dus als basis-kettingbreuk schrijven!!!!!
Kortom: Elke breuk is met zulke wijzergetallen weer te geven.

Geef van de volgende breuken de wijzergetallen:

¹⁵⁵/₆₇

{2 ; 3, 5, 4}

²³³/₇₂

{3 ; 4, 4, 4}

⁶⁵/₅₆

{1 ; 6, 4, 9}

³⁰/₄₃

{0 ; 1,2,3,4}

Schrijf de volgende kettingbreuken als gewone breuk:

⁸⁷/₃₈

¹⁴⁵/₁₂₂

⁸²/₂₅

¹¹/₂₆

2. Oneindige Kettingbreuken.

Het kan natuurlijk ook gebeuren dat zo'n kettingbreuk alsmaar doorgaat. Een oneindig grote kettingbreuk. Die zul je dus NIET als een gewone breuk kunnen schrijven (we zagen bovenaan deze les dat gewone breuken eindige kettingbreuken opleveren), dus die stelt een irrationaal getal voor.
Nou zijn er weer twee soorten: sommige oneindige kettingbreuken gaan zich herhalen; die noemen we periodiek. Anderen doen dat niet, daar blijft het chaos.

Nou blijkt het zo te zijn dat periodieke kettingbreuken altijd als wortel zijn te schrijven! Het bewijs is vrij eenvoudig, ik zal met een voorbeeldje laten zien hoe het werkt.
Neem de oneindige kettingbreuk {0; 2, 3, 4, 2, 3, 4, 2, 3, 4,...}. Laten we hem voorlopig X noemen.
Dan geldt dus:

Maar omdat die breuk zich herhaalt is er iets aparts aan de hand:

Daar in dat rode rondje staat de breuk X zélf weer (omdat hij zich herhaalt), dus kunnen we een vergelijking zoals rechts opstellen. En die is eenvoudig op te lossen, kijk maar:

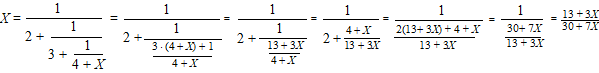dus
X(30 + 7X) = 13 + 3X
⇒ 7X² + 27X - 13 = 0
⇒ X = -²⁷/₁₄ + ¹/₁₄√(1093) (≈ 0,432896465...)
En dat kan niet alleen in dit voorbeeld, maar altijd!
Immers: omdat de breuk zich herhaalt kun je altijd zo'n X ergens na een poosje in de breuk terugvinden. En bij het oplossen van de vergelijking hebben we alleen maar met lineaire vergelijkingen te maken. Dus eindigen we altijd met een ABC-formule, en dat geeft een wortel als antwoord.

Welke "echte" getallen zijn gelijk aan de volgende periodieke kettingbreuken?

{1; 2, 4, 2, 4, 2, 4,...}

-1 + √6

{0; 1, 2, 3, 1, 2, 3, 1, 2, 3,...}

-⁴/₃+¹/₃√37

{4; 5, 5, 5, 5, 5, .....}

³/₂+¹/₂√29

Onderzoek de kettingbreuken van de vorm {0; a, a, a, ...} en leg uit welke wortels er mee kunnen worden weergegeven. Beperk je onderzoek voor 0 < a < 6.

-¹/₂+ ¹/₂√5
-1 + ¹/₂√8
-1¹/₂ + ¹/₂√13
-2 + ¹/₂√20
-2¹/₂+ ¹/₂√29
-3 + ¹/₂√40

Kettingbreuk als benadering.

Zo'n kettingbreuk is meteen een efficiënte manier om een getal te benaderen.
Neem bijvoorbeeld die -²⁷/₁₄ + ¹/₁₄√(1093) van hierboven, die als kettingbreuk gelijk is aan {0; 2,3,4,2,3,4,...}
Hoe meer getallen je van de kettingbreuk dan neemt, des te beter nadert de waarde naar de echte (≈ 0,432896465...)
Kijk maar:

kettingbreuk:	benadering:	afwijking:
	0,5	0,07
	0,42857...	0,004
	0,43333...	0,0004
	0,43283...	0,00006
	0,43290...	0,000004
enz.

3. Beroemde Kettingbreuken.

De allerberoemdste is meteen de eenvoudigste: het is de breuk {1; 1, 1, 1, 1, 1...}
Als je er op de manier van hierboven een gewoon getal van probeert te maken dan krijg je de vergelijking X = 1 + ¹/_X
Dat geeft X² - X - 1 = 0 met als oplossing X = ¹/₂ + ¹/₂√5, en dat is een oude bekende: de Gulden Snede: F
De gulden snede is een erg beroemd getal dat op vele plekken in de wiskunde opduikt. Hier kun je er meer over lezen.

Nog een paar kettingbreuken waar een mooi patroon in zit:

• tan(1) = {1; 1,1,3,1,5,1,7,1,9,1,11,...}

• e = {2; 1,2,1,1,4,1,1,6,1,1,8,1,1,10,...}

• √2 = {1; 2, 2, 2, 2, 2, 2,...}

Natuurlijk is er ook een kettingbreuk die het getal π snel benadert. Dat is π = {3; 7, 15, 1, 292, 1, 1, ...}
Dat geeft als benadering voor π achtereenvolgens: 3, ²²/₇, ³³³/₁₀₆, ³⁵⁵/₁₁₃, en dat nadert erg snel naar π.
Maar dat is natuurlijk een erg lelijke aperiodieke kettingbreuk. Er zijn veel mooiere kettingbreuken die ook π benaderen, en die wel een prachtige regelmaat en schoonheid vertonen.
Kijk en bewonder:

Een toepassing: Gehele oplossingen zoeken.

Er zit een regelmaat in de serie breuken die je krijgt door een kettingbreuk steeds verder uit te rekenen.
Neem bijvoorbeeld de kettingbreuk {1; 2, 3, 4, 5, ...}
Laten we die gaan benaderen, met een serie breuken.
Dat geeft:

kettingbreuk	gewone breuk
{1}	¹/₁
{1; 2}	³/₂
{1; 2, 3}	¹⁰/₇
{1; 2, 3, 4}	⁴³/₃₀
{1; 2, 3, 4, 5}	²²⁵/₁₅₇

Er zit regelmaat in die tweede kolom. Zie je al welke regelmaat?
Kijk naar de tellers en de noemers apart.
De tellers zijn 1 - 3 - 10 - 43 - 225 en de noemers 1 - 2 - 7 - 30 - 157

RARARA......

Misschien helpt het als we het iets algemener bekijken.
Stel dat we de eerste drie breuken hebben berekend (¹/₁ en ³/₂ en ¹⁰/₇)
Laten we nu een extra getal aan de kettingbreuk toevoegen, maar niet 4 zoals hierboven, maar een willekeurige x.
Dat geeft:

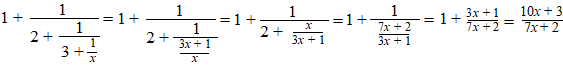Dus als we x toevoegen, en we hebben al de breuken ¹/₁ en ³/₂ en ¹⁰/₇ dan geeft dat de nieuwe breuk ^{(10x + 3)}/_{(7x + 2)}Zie je het nu?
Nog niet??

Elke nieuwe breuk is opgebouwd uit de twee vorigen, volgens deze regel:

Als je hebt de breuken

en je voegt aan de kettingbreuk getal a_ntoe, dan krijg je breuk

Dat geeft een lekkere snelle manier om kettingbreuken te gaan benaderen met gewone breuken. Hoef je niet steeds al dat breuken samennemen en delen door een breuk uit te voeren.
Voorbeeld: neem de kettingbreuk {2; 6, 5, 4, 3, 2}
Dat geeft dan deze rij breuken: ²/₁ en ¹³/₆ om mee te beginnen,
en dan in sneltreinvaart: ⁶⁷/₃₁ en ²⁸¹/₁₃₀ en ⁹¹⁰/₄₂₁ en ²¹⁰¹/₉₇₂ (reken het zelf maar na)

Als we deze rekenregel willen doorvoeren tot en met breuk nummer nul, dan moeten we T₀ en N₀ handig kiezen.
Er moet dan namelijk gelden: T₂ = a₂T₁ + T₀ = a₂ • a₁ + T₀ en ook N₂ = a₂N₁ + N₀ = a₂ • 1 + N₀
Daaruit volgt T₀ = 1 en N₀ = 0

De rij breuken begint altijd met de "breuk" ¹/₀

De volledige rij zou dan worden: ¹/₀ ²/₁ ¹³/₆ ⁶⁷/₃₁ enz.

Nu is er met T_nN_{n + 1} - T_{n + 1}N_n iets bijzonders aan de hand, kijk maar:
T_nN_{n + 1} - T_{n + 1}N_n= T_n(a_n₊₁ • N_n+ N_{n - 1}) - (a_n_{- 1} • T_n + T_{n - 1}) N_n = -(T_{n - 1}N_n - T_nN_{n -1})
Dus bijvoorbeeld T₄N₅ - T₅N₄ = -(T₃N₄ - T₄N₃) = +(T₂N₃ - T₃N₂) = -(T₁N₂ - T₂N₁)
Elke keer als je n eentje lager maakt komt er een minteken voor deze uitdrukking.
Dan kun je ook in één keer schrijven: T_nN_{n
+ 1} - T_{n + 1}N_n= (-1)ⁿ • (T₀N₁ - T₁N₀) = (-1)ⁿ

T_nN_{n + 1} - T_{n
+ 1}N_n=(-1)ⁿ

Maar ehh...waar blijft nou die toepassing?

Die komt nu.

Stel dat we willen weten welke gehele oplossingen de vergelijking ax + by = 1 heeft.
Dan kun je de kettingbreuk ^a/_b gaan uitschrijven als hierboven met zo'n serie van n breuken, waarvan de laatste dan gelijk zal zijn aan ^a/_b.
Dus T_n = a en N_n = b
Het wordt pas interessant als je de één na laatste van die serie breuken bekijkt.
Kies x = (-1)ⁿ • N_{n - 1} en y = -(-1)ⁿ • T_{n - 1} dan voldoen die x en y aan de bovenstaande vergelijking!!!!

Kijk maar:
ax + by
= T_n • (-1)ⁿ • N_{n
- 1} - N_n • (-1)ⁿ • T_{n - 1}
= (-1)ⁿ • (T_n • N_{n
- 1} - N_n • T_{n - 1})
= (één n hoger gaan geeft een minteken)   -(-1)ⁿ • ( T_n+1 • N_n - N_n+1 • T_n)
= (haal een minteken buiten haakjes)    (-1)ⁿ • ( T_n • N_n+1 - N_n • T_n+1)
= (met de eigenschap hierboven)   (-1)ⁿ • (-1)ⁿ = (-1)²ⁿ = 1
q.e.d.

Conclusie:

ax + by = 1 heeft als oplossing x = (-1)ⁿ • N_{n - 1} en y = -(-1)ⁿ • T_{n -
1}

Voorbeeld: geef een oplossing met gehele getallen van de vergelijking 49x + 38y = 1
De breuk ⁴⁹/₃₈ is als kettingbreuk {1; 3, 2, 5}. Reken dat maar na.
De serie benaderende breuken is dan: ¹/₀ en ¹/₁en ⁴/₃ en ⁹/₇ en ⁴⁹/₃₈
De één na laatste breuk is ⁹/₇ en dat is die bij n = 4.
Dat geeft x = (-1)⁴ • 7 = 7 en y = -(-1)⁴ • 9 = -9
Inderdaad geldt dat 49 • 7 + 38 • -9 = 1

Nog algemener.

Nu kunnen we ineens ook de vergelijking ax + by = c oplossen.
Dat gaat zo: deel alles door c, dan vind je de vergelijking   a(^x/_c) + b(^y/_c) = 1
Met de methode hierboven kun je nu ^x/_c en ^y/_c vinden, en dan heb je dus ook x en y

Voorbeeld: geef een oplossing met gehele getallen van de vergelijking   61x + 27y = 5
De breuk ⁶¹/₂₇ is als kettingbreuk {2; 3, 1, 6}. Reken dat maar na.
De serie benaderende breuken is dan:   ¹/₀ en ²/₁en ⁷/₃ en ⁹/₄ en ⁶¹/₂₇De één na laatste breuk is ⁹/₄ en dat is die bij n = 4.
Dat geeft ^x/₅ = 4 en   ^y/₅ = -9 dus de oplossingen zijn x = 20 en y = -45
Inderdaad geldt dat 61 • 20 + 27 • -45 = 5

Nog Nog Nog algemener!

Met de bovenstaande methode vind je precies één oplossing van zo'n vergelijking. Dat noemen we de particuliere oplossing. Maar er zijn natuurlijk nog veel méér oplossingen.
Die kun je vinden met de volgende stelling:

als x_P, y_P een oplossing is van ax + by = c, dan is x_P + k • b, y_P - k • a óók een oplossing.

Daarbij is k een willekeurig geheel getal.
Het bewijs kan in één regel:
a(x_P + kb) + b(y_P - ka) = ax_P + akb + by_P - akb = ax_P + by_P = 1. qed.

Laatste voorbeeld: Zoek alle gehele positieve oplossingen van 8x + 13y = 210
De breuk ⁸/₁₃ is als kettingbreuk {0; 1, 1, 1, 1, 2}. Reken dat maar na.
De serie benaderende breuken is dan:   ¹/₀ en ⁰/₁en ¹/₁ en ¹/₂ en ²/₃ en ³/₅en ⁸/₁₃
De één na laatste breuk is ³/₅ en dat is die bij n = 6.
Dat geeft ^x/₂₁₀ = 5 en   ^y/₂₁₀ = -3 dus de oplossingen zijn x = 1050 en y = -630
De algemene oplossingen zijn dan   x = 1050 + 13k en y = -630 - 8k
Als x > 0 dan moet 1050 + 13k > 0 ofwel k > -80,8...
Als y > 0 dan moet -630 - 8k > 0 ofwel k < -78,7...
Dat geeft twee mogelijkheden: k = -79 en k = -80 en de oplossingen zijn (x = 23 en y = 2) en (x = 10 en y = 10)

Twee broertjes lopen mee aan een sponsorloop. Ze gaan daarvoor de deuren langs om van buren een bepaald bedrag per gelopen rondje te krijgen.
De oudste krijgt €1,50 per rondje en de jongste €0,80
Na afloop hebben de jongens samen €25,90 aan geld verdiend.
Hoeveel rondjes hebben ze gelopen?

5 en 23
of 13 en 8

De lijn y = 16¹/₁₁ - 1⁵/₁₁x loopt door het eerste kwadrant.
Onderzoek hoeveel roosterpunten op de lijn liggen.

één: (9, 3)