|
|
 |
|
Valkuilen.... |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
 |
We hebben intussen geleerd hoe je
een regressielijn opstelt en hoe je de correlatiecoŽfficiŽnt ervan
berekent.
Het wordt pas gevaarlijk als je daar conclusies aan gaat verbinden. Er
zijn een boel valkuilen en interpretatieverschillen te maken rondom onze
r.
In deze les zullen we een aantal, veel voorkomende
fouten/misverstanden/valkuilen de revue laten passeren. |
| |
|
|
Valkuil 1 : Verschillende
deelpopulaties. |
| |
|
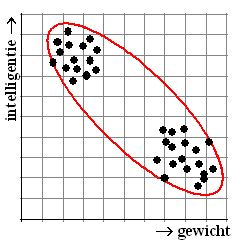
Gijs en Karel onderzoeken samen of er een
verband is tussen de intelligentie en het lichaamsgewicht van een aantal
beesten. Ze hebben een testje ontworpen van hoe snel een beest iets
leert en daarmee meten ze de intelligentie. Ze vinden de puntenwolk
hiernaast.
Berekeningen leveren een best grote negatieve correlatie.
"Hoe zwaarder des te dommer" zou je kunnen concluderen.
Totdat je ziet dat die puntenwolk van Gijs en Karel eigenlijk bestaat
uit twee aparte wolkjes! Wat hebben ze gedaan? Ze hebben hun experiment
op paarden ťn op honden uitgevoerd en alle gegevens op ťťn hoop gegooid. |
 |
| |
|
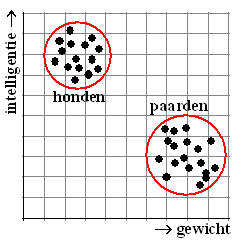
Honden zijn nou eenmaal slimmer dan paarden,
maar dat heeft niets te maken met het feit dat ze lichter zijn.
Als je de puntenwolken voor de honden en de paarden apart bekijkt, zoals
hiernaast, dan zie je dat er van die correlatie niets overblijft! |
 |
| |
|
| |
|
|
Valkuil 2: Selectie van de
steekproef |
| |
|
Dit is eigenlijk het omgekeerde van de vorige
valkuil.
Stel dat Gijs en Karel doorgaan met hun IQ-onderzoek, en deze keer
willen onderzoeken of er verband is tussen de draagtijd van een baby
(het aantal dagen tussen verwekt worden en geboren worden) en het IQ van
het geboren kind.
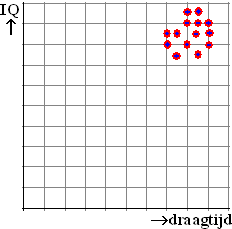
Gijs en Karel zitten beiden op het VWO en meten bij alle klasgenoten het
IQ en de draagtijd.
Dat geeft de puntenwolk hiernaast, en ze vinden maar een erg kleine
correlatie. |
 |
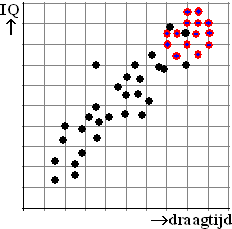
Maar ja, ze bekijken helaas maar een erg
select groepje: alleen maar VWO-leerlingen, en die hebben gemiddeld een
hoog IQ. Misschien zag de puntenwolk voor kinderen van alle leerniveaus
er eigenlijk wel uit als hiernaast en was er best een redelijk grote
correlatie tussen draagtijd en IQ!
In deze tweede grafiek zie je dat er voor alle punten wel een redelijk
grote correlatie is, maar voor die rode punten niet!
Jammer voor Gijs en Karel!
Ze zullen niet de NOBELprijs voor dit onderzoek ontvangen.... |
 |
| |
|
| |
|
|
Valkuil 3: Uitschieters. |
| |
|
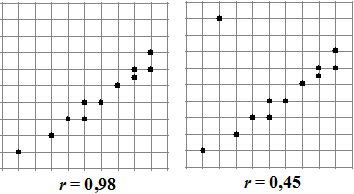
Eťn punt dat erg ver van een verder bijna
perfecte lijn afligt geeft een forse daling in de correlatiecoŽfficiŽnt.
Dat komt natuurlijk omdat die afwijking in het kwadraat wordt genomen,
en dus relatief erg zwaar meetelt. Zo'n "uitschieter" kan heel
goed het gevolg van een meetfout zijn.
Kijk maar naar de figuren hiernaast hoeveel r daardoor kan veranderen.
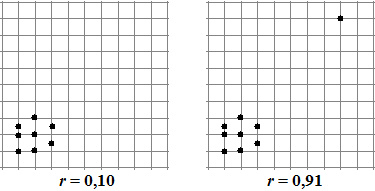
Het kan ook voorkomen dat een uitschieter juist zorgt voor een grotere
r!
Probeer je daar ook eens een puntenwolk bij voor te stellen, en kijk
daarna of je iets in je hoofd had als hieronder. |
 |
| |
|
|
 |
| |
|
|
Valkuil 4: Kromlijnige
samenhang. |
| |
|
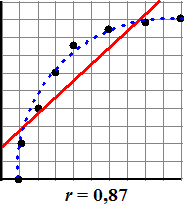
De correlatiecoŽfficiŽnt r hoort bij een
lineair verband. Maar de punten van onze puntenwolk zouden natuurlijk
ook best op een kromme grafiek kunnen liggen!
Hiernaast is de regressielijn berekend voor de puntenwolk.
Dat is de rechte rode lijn, en die geeft r = 0,87. Redelijk, maar niet
super....
Maar als je de puntenwolk bekijkt, dan zie je in ťťn oogopslag dat een
kromme zoals die blauwe er veel beter bij past!
Later zullen we zien hoe je betere krommen bij deze puntenwolk kunt
maken. Voorlopig is het genoeg om je te realiseren dat die rechte rode
lijn niet zo'n goeie is. |
 |
| Een manier om zulke systematische afwijkingen
op het spoor te komen is het maken van een zogenaamde residuplot. |
|
| |
|
|
residuplot |
| |
|
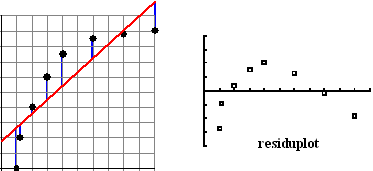
Ik hoop dat je nog weet wat de residuen
waren: het waren die verticale afwijkingen tussen de punten van de
puntenwolk en de regressielijn. Die verticale blauwe lijntjes in de
linkerfiguur hiernaast.
Je kunt ze op je rekenmachine vinden en in een lijst zetten via
2nd
-
LIST
-
7:RESID
-
STO
-
2nd
-
L3
Daarna kun je ze plotten met
STATPLOT
en dan
Xlist:
L1 en
Ylist:
L3
Dat is hiernaast gebeurd in de figuur rechts. Zo'n figuur heet een
residuplot. |
 |
| Als de puntenwolk nou inderdaad
bij een rechte lijn past, dan zullen die residuen willekeurig verdeeld
zijn. |
Zodra je er een patroon in
herkent; ťťn of andere regelmaat, dan is dat een aanwijzing dat er "iets
aan de hand is", en dat een rechte lijn misschien niet het best past bij
jouw puntenwolk.
In zulke gevallen zul je een ander soort verband moeten zoeken. Hoe dat
precies moet, dat zullen we in een latere les bekijken. |
| |
|
|
Valkuil 5: Vertraging |
| |
|
Een onderzoeker meet bij een aantal
proefpersonen
de hoeveelheid hashgebruik en ook het IQ. Hij vraagt zich namelijk af of je van veel
hash roken
misschien dommer wordt.....
Helaas vindt hij geen correlatie....
Kijk maar:
| persoon |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
| hashgebruik (gram) |
0.0 |
0.5 |
0.6 |
1.0 |
1.7 |
1.8 |
1.9 |
2.5 |
2.6 |
2.8 |
3.3 |
3.6 |
3.8 |
4.0 |
4.3 |
4.6 |
| IQ |
96 |
84 |
114 |
104 |
87 |
100 |
109 |
94 |
117 |
105 |
88 |
115 |
102 |
110 |
86 |
97 |
|
| |
|
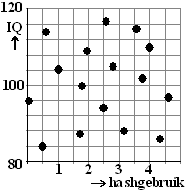
Hij vindt een teleurstellende r = 0,047.
Dat is ook wel te zien aan de puntenwolk hiernaast: vrij
willekeurig verdeeld allemaal.
Helaas, het onderzoek kan de prullenbak in.
Een andere onderzoeker leest een paar jaar later over dit onderzoek en gelooft het
niet: zij is ervan overtuigd dat hash roken mensen dommer maakt,
en ze denkt gewoon dat de eerste onderzoeker meetfouten heeft
gemaakt. Daarom herhaalt zij dit onderzoek bij dezelfde groep
proefpersonen.
Zij vindt de volgende gegevens: |
 |
| |
|
| persoon |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
| hashgebruik (gram) |
0.0 |
2.7 |
2.4 |
3.5 |
1.7 |
1.8 |
4.8 |
0.5 |
2.6 |
2.8 |
0.9 |
1.5 |
2.0 |
4.0 |
4.3 |
4.6 |
| IQ |
116 |
108 |
124 |
108 |
112 |
100 |
112 |
93 |
100 |
92 |
84 |
89 |
92 |
88 |
83 |
90 |
|
| |
|
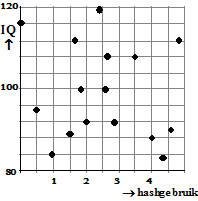
Vol goede hoop maakt zij de puntenwolk
hiernaast.
Helaas!
Alweer geen verband te vinden. Nu is r = -0,12. Erg laag dus. De
punten zijn nog steeds vrij willekeurig verspreid.
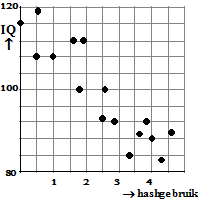
Maar het wordt pas interessant als je een puntenwolk maakt van
het eerste hashgebruik (dat van de eerste onderzoeker)
tegen het laatste IQ (dat van de laatste
onderzoeker)!!!
Dat geeft de puntenwolk hieronder. |
 |
|
 |
|
| |
|
|
En daarin is ineens wťl een
aardige hoge (negatieve) correlatie te zien! De
correlatiecoŽfficiŽnt van deze laatste puntenwolk is maar liefst
r
=
-0,90.
Wat is hier aan de hand?
Het lijkt erop dat veel hashgebruik inderdaad het IQ lager maakt, maar
dat effect komt pas een paar jaar later. Er is wel een correlatie, maar
die is vertraagd. |
| |
|
Valkuil 6: Causaliteit. |
| |
|
| Dat is een zo veel voorkomende en
belangrijke valkuil dat we er een aparte les aan zullen besteden. |
| |
|
| |
|
|
OPGAVEN |
| |
|
| 1. |
Welk van de valkuilen zouden bij de volgende
onderzoeken een rol kunnen spelen? |
| |
|
|
|
| |
a. |
Onder een aantal topschaatsers wordt
een onderzoek gedaan naar de bloeddruk en de hoeveelheid koffie
die men drinkt. Men vindt een kleine correlatie. |
| |
|
|
|
| |
b. |
Van een aantal mannen tussen 4 en 70
jaar wordt het reactievermogen gemeten. Er blijkt haast geen
correlatie tussen leeftijd en reactiesnelheid. |
| |
|
|
|
| |
c. |
Onder alle werknemers van een groot
bedrijf wordt gemeten hoeveel make-up men gebruikt en hoeveel
bier men drinkt. Er blijkt een heel erg sterke negatieve
correlatie te zijn. |
| |
|
|
|
| |
d. |
Van leerlingen die een erg slechte
tijd op de 100 meter hardlopen hadden wordt de bloeddruk
gemeten. Er wordt gezocht naar een correlatie tussen de
bloeddruk en de 100 m tijd. |
| |
|
|
|
| |
e. |
Een frisdrankfabrikant houdt goed
bij hoeveel minuten reclame er voor zijn merk op een bepaalde
dag wordt uitgezonden, en hoeveel frisdrank wordt verkocht. Hij
vindt haast geen correlatie, dus besluit maar met de reclame te
stoppen. "Weggegooid geld" is zijn commentaar. |
| |
|
|
|
| |
|
|
|
| 2. |
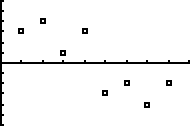
a. |
Frank heeft van een puntenwolk de
regressielijn opgesteld en er zelfs met zijn GR een residuplot
bij gemaakt. Die residuplot staat hiernaast.
Leg duidelijk uit hoe je daaraan kunt zien dat Frank
waarschijnlijk een fout heeft gemaakt bij het opstellen van de
regressielijn. |
|
| |
|
|
|
| |
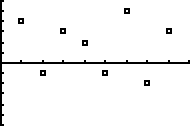
b. |
Zijn broertje Leo zegt: "Haha, dit
lijkt nergens op, Frank, laat mij maar even". Hij produceert
vervolgens de residuplot hiernaast.
Leg duidelijk uit hoe je kunt zien dat ook Leo's methode niet
klopt. |
|
| |
|
|
|
| 3. |
In de volgende tabel staan de
gemiddelde prijzen (in duizenden euro) van alleenstaande
woningen in een bepaalde maand, en ook de hoogte van de
hypotheekrente (in %). Het lijkt aannemelijk dat een lage
hypotheekrente een hoge huizenprijs tot gevolg heeft. |
| |
|
|
|
| |
| maand |
jan |
feb |
mrt |
apr |
mei |
jun |
jul |
aug |
sep |
okt |
nov |
dec |
| gemiddelde rente (r) |
6.0 |
7.6 |
8.9 |
8.5 |
6.2 |
4.1 |
3.7 |
4.5 |
5.8 |
7.2 |
8.6 |
8.7 |
| gemiddelde prijs (p) |
200 |
210 |
260 |
330 |
350 |
320 |
250 |
210 |
200 |
250 |
400 |
450 |
|
| |
|
|
|
| |
a. |
Bereken de correlatiecoŽfficiŽnt. |
| |
|
|
|
| |
b. |
Teken in ťťn figuur de grafieken van
p(t) en r(t) met
t de tijd in maanden. Leg met deze figuur uit dat er
waarschijnlijk sprake is van een vertraagde reactie tussen r
en p. |
| |
|
|
|
| |
c. |
Bereken opnieuw de
correlatiecoŽfficiŽnt als je rekening houdt met deze vertraagde
reactie. |
| |
|
|
|
| |
|
|
|
| 4. |
Cook's Afstand.
Een manier om uitschieters te berekenen (in plaats van naar de
puntenwolk te kijken) is het berekenen van Cook's afstand. Dat
werkt als volgt:
Stel dat yj de voorspelling voor punt j
is als de regressielijn met alle punten wordt berekend.
Stel dat yj-i de voorspelling voor
punt j is als de regressielijn met alle punten behalve
punt i wordt berekend.
Dan is Cook's afstand Di van punt i
gelijk aan: |
| |
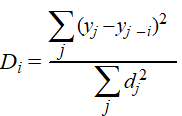 |
| |
|
|
|
| |
Daarbij was dj het
residu van punt j, weet je nog?
Als vuistregel wordt een punt als een uitschieter beschouwd als
Di groter of gelijk aan 1 is. |
| |
|
|
|
| |
a. |
Bereken Cook's afstand voor de
punten (1,1) en (2,10) van de volgende tabel: |
| |
|
|
|
| |
|
| x |
1 |
2 |
2 |
3 |
4 |
5 |
| y |
1 |
3 |
10 |
2 |
4 |
4 |
|
| |
|
|
|
| |
b. |
Laat zien hoe de
correlatiecoŽfficiŽnt verbetert als de uitschieter weggelaten
worden. |
| |
|
|
|
| 5. |
Van een aantal topsporters is de
systolische bloeddruk (B, in mm Hg) en de hartslag (H, in
slagen/min) gemeten.
Dat gaf de volgende tabel: |
| |
|
|
|
| |
| H |
50 |
53 |
55 |
57 |
58 |
61 |
62 |
65 |
69 |
70 |
60 |
54 |
| B |
100 |
110 |
106 |
114 |
126 |
119 |
121 |
130 |
122 |
136 |
120 |
91 |
|
| |
|
|
|
| |
a. |
Bereken van deze gegevens de
correlatiecoŽfficiŽnt. |
|
| |
|
|
|
| |
b. |
De grootte van de
correlatiecoŽfficiŽnt hangt niet af van wat je als oorzaak en
wat als gevolg beschouwt. Leg met formule(s) uit waarom dat zo
is. |
| |
|
|
|
| |
c. |
Stel dat er inderdaad een verband is
tussen hartslag en bloeddruk.
Als je niet alleen topsporters, maar iedereen in dit onderzoek
zou betrekken, verwacht je dan een grotere of een kleinere
correlatiecoŽfficiŽnt? Leg duidelijk uit waarom. |
| |
|
|
|
| |
d. |
Welk punt levert de grootste
bijdrage aan de som van de kwadraten van de residuen en hoe groot is die
bijdrage? |
| |
|
|
|
| |
|
|
|
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
 |