Genoeg van dat gegok!

© h.hofstede (h.hofstede@hogeland.nl)
   
Bij het oplossen van differentiaalvergelijkingen van de eerste orde en eerste graad volgden we de methode om één oplossing te "raden" of te  "proberen" (de particuliere oplossing   p(x)), en daarna de homogene vergelijking op te lossen (homogene oplossing h(x)).
De algemene oplossing was dan y =  p(x) + h(x)
Nou is dat vinden van die particuliere oplossing wel een zwak punt in dit verhaal. Meestal werd er gegeven welke soort oplossing je moest proberen, of moest je raden aan de hand van een lijnelementenveld. Nogal vaag allemaal.

Dat kan beter!

Laten we uitgaan van de differentiaalvergelijking  y' + f(x) • y = g(x)
(Vergeleken met onze basisvorm hebben we  f(x) vervangen door -f(x) dat komt straks beter uit)
Deze hele vergelijking gaan we nu vermenigvuldigen met één of andere functie  h(x). De reden daarvan komt zo meteen. Even geduld. 
Als we dat doen staat er    h(x) • y' + h(x) • f(x) • y = h(x) • g(x)
Dat lijkt alleen maar moeilijker te worden.
Maar stel nou dat het ons lukt die h(x) zó te kiezen dat  h(x) • f(x) = h'        .........(1)

Stel dat het lukt....

Dan  staat er (we laten voor het gemak even alle x-en tussen haakjes staan weg)   h • y' +  h' • y =  h • g
En dat stuk aan de linkerkant moet je bekend voorkomen!
Daar staat  (hy)'   de productregel!!!

Dus de vergelijking geeft  (hy)'  = hg
Primitiveren:   hy = ∫hg   +  c    (de constante c hoeft maar aan één van beide kanten te staan)
Delen door h geeft dan de oplossing:   
   

   
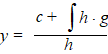Dus áls we zo'n wonderbaarlijke functie h(x) kunnen vinden die voldoet aan (1):   h(x) • f(x) = h'   dan is het klaar!
Maar dat is gelijk aan  h'/h = f   ofwel   1/h • h' = f   en daarvan kunnen we weer makkelijk beide kanten primitiveren:
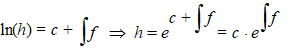Daarbij is weer aan één kant een c gezet, en is  ec   later weer een nieuwe c genoemd.

Laatste hindernis.

We hebben nu een oplossing maar nog wel met twee constanten. Die twee c's zijn vast niet gelijk. Er staat er eentje in h en ook eentje in de oplossing voor y.
Dat lost zichzelf op als we de formule voor h invullen in die voor y:

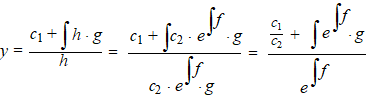
En dus is er maar één nieuwe constante over:  c = c1/c2
Samengevat:

   
Voorbeeld 1.

Gegeven is de differentiaalvergelijking   y'  =  10 - 5y.  Geef de algemene oplossing.
Dat geeft  y' + 5y = 10
 ∫ f  = 5x, dus de integrerende factor is  h = e5x
 ∫ hg = ∫10e5x = 2e5x
De oplossing is dan:

 
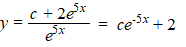   (.......Eitje!!)  
   
Voorbeeld 2.

Gegeven is de differentiaalvergelijking   xy'  + y  =  3x2 - 4 + 1/x.  Geef de algemene oplossing.
Delen door x:   y'  + 1/x • y = 3x - 4/x + 1/x2
 ∫ f =  lnx  dus de integrerende factor is  h = elnx = x
 ∫ hg = ∫ (3x2 - 4 + 1/x) = x3 - 4x + lnx
De oplossing is dan:

   
   
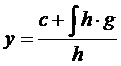  OPGAV EN
   
1. Geef de algemene oplossing van de volgende differentiaalvergelijkingen:
       
  a. cosx • dy/dx = cos2x - sinx • y       (bedenk dat ∫tanx = -ln(cosx))

c • cosx + x • cosx

       
  b. xy'  = 2y + 3x4 + 2

y = cx-2 + 11/2x4 - 1

       
  c. dy/dx + 2xy = 2x

y = 1 + c • e-x²
       
  d. 2x• dy/dx + y = 2x√x

y = c/√x + 1/2x√x
       
  e. y' - 2y =  e3x

y = ce2x + e3x
       
  f. x2 y'  + xy = x2 + 1

y = c/x + 1/2x + lnx/x
       
  g. y' + y/(x - 1) = 1/(x - 1)(x + 3)

y = c/(x - 1) + ln(x + 3)
       
  h. (1 + x2) • y'  + 2xy = 1 + x2   
bedenk daarbij dat  ln(1 + x2) een primitieve is van  2x/(1 + x2)

y = 1/(1 + x2) • (x + 1/3x3 + c)
       
  i. y' x - 3y = 7x

y = -31/2x + cx3
       
  j. y'  + 3y = e-3x

y = (x + c)/e3x
       
  k. xy' + 2y = 8x2

y = c/x2 + 2x2
       
  l. xy'  - 4y = x6ex

y = x5ex - x4ex+ cx4
       
  m. cosx • y'  + ysinx = 2cos3xsinx - 1  
       
     

© h.hofstede (h.hofstede@hogeland.nl)