|
|
 |
|
De Hyperbool. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
De hyperbool is de laatste
conflictlijn die we gaan bestuderen. Het is, net als bij de ellips, de
conflictlijn van een punt met een cirkel, maar nu ligt dat punt buiten
de cirkel.
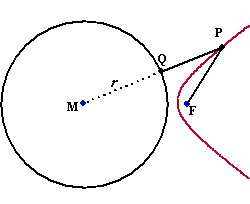
De conflictlijn ziet eruit als de rode lijn hiernaast. Daarin is PQ = PF.
Maar omdat PQ = MP - r
geldt MP - r = PF
Dat geeft MP - PF = r
Bij de ellips ontdekten we dat we de hele figuur konden spiegelen zodat
ook M de rol van brandpunt kan hebben. Dat gaan we bij deze hyperbool
ook doen, maar anders dan bij de ellips levert dat niet dezelfde ellips,
maar een tweede tak op: |
 |
| |
|
|
 |
| |
|
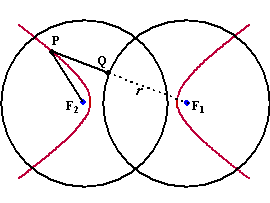
Voor die tweede tak geldt dan net
als bij de eerste tak ook F1P - F2P = r
We zullen straks zien dat beide takken in één eenvoudige vergelijking
zijn weer te geven. Ze zijn nu al in één regel samen te vatten door te
stellen: |F1P
- F2P|
= r .
Aan de figuur hierboven zie je al dat de afstand tussen de toppen van de
hyperbool gelijk is aan r. |
| |
|
|
Hyperbool: | d(P, F1)
- d(P, F2) |
= r |
|
| |
|
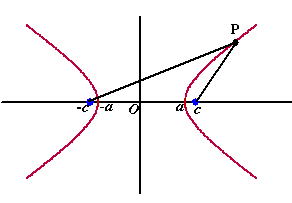
We gaan een vergelijking maken door het
"midden" van de hyperbool in de oorsprong te leggen en de brandpunten in
(c,0) en (-c, 0).
Stel de plaats van de toppen (-a, 0) en (a,0) dan is dus
r = 2a
Als P het punt (x, y) is, dan geldt tweemaal
Pythagoras:
d(P, F1) = √((x
- c)2 + y2)
d(P, F2) = √((x
+ c)2 + y2)
Dus geldt: √((x +
c)2 + y2) -
√((x
- c)2
+ y2) = 2a
In de volgende opgave ga je, net als bij de ellips, deze
vergelijking wat "mooier" schrijven. |
 |
| |
|
| 1. |
a. |
Begin met de vergelijking hierboven:
√((x + c)2
+ y2) - √((x
- c)2 + y2) = 2a
Breng nu de tweede wortel naar de rechterkant en kwadrateer
vervolgens beide kanten.
Laat aan de rechterkant alleen de wortel staan en breng de rest
naar de linkerkant.
Toon aan dat dat geeft: cx
- a2
= a√((x -
c)2 + y2) |
| |
|
|
|
| |
b. |
Kwadrateer nu opnieuw beide kanten en breng
alles met een x of y naar links, en de rest naar
rechts.
Toon aan dat je dan krijgt: x2 • (c2
- a2)
- a2y2
= a2c2
- a4
|
| |
|
|
|
| |
c. |
Noem nu c2
-
a2 = b2 (dat kan
altijd omdat c > a) en laat zien dat deze
vergelijking dan te schrijven is als:
|
|
En het mooie is: Als je
punt P op de linkertak kiest dan leidt dat uiteindelijk tot precies
dezelfde vergelijking! Je kunt dat al wel aanvoelen doordat in de
vergelijking de x alleen maar in de vorm x2
voorkomt, dus zal de figuur symmetrisch ten opzichte van de y-as
zijn, en dat is die ene tak niet! (Ga zelf de
afleiding van de formule voor die andere tak maar na, als je zin hebt,
het gaat precies zo als hierboven).
De grote vraag is nu eigenlijk : Wat stelt die b nou voor?
Bij de ellips gaf b de plaats van de snijpunten met de y-as, maar die zijn
er nu niet! Hoe zit dat???
Toch is het eigenlijk net als bij de ellips. Het getal
b geeft de plaats van de toppen als je de brandpunten op de y-as
kiest (die zijn dan (0, c) en (0, -c)). De
vergelijking wordt in dat geval:
|
Je kunt deze formule makkelijk
net zoals hierboven afleiden, maar ik hoop dat je hem nu al "logisch"
vindt. Ook die -1. Als de toppen op de y-as liggen dan moet x
= 0 immers als oplossing geven y =
±b....
Samengevat: |
| |
|
|
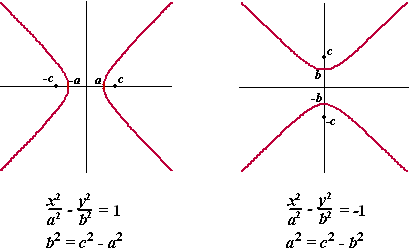 |
| |
|
|
Translaties. |
| |
|
Natuurlijk kun je ook deze
hyperbolen weer verschuiven. Dat gaat op precies dezelfde manier als bij
cirkels en ellipsen en parabolen. Door x te vervangen door x
± a schuif je de hyperbool a
naar links/rechts en door y te vervangen door y ± a
schuif je hem a omlaag/omhoog.
Omgekeerd kun je door kwadraat afsplitsen bij een gegeven
vergelijking achterhalen wat die a is geweest dus hoe de
hyperbool is verschoven.
Een voorbeeld zal wel genoeg zijn, denk ik...
Voorbeeld:
Geef de coördinaten van brandpunten en toppen van de hyperbool 36x2
- 25y2
- 100y + 325 = 0
oplossing:
36x2 - 25(y2 + 4y) + 325 = 0
36x2 - 25(y2 + 4y + 4
- 4)
+ 325 = 0
36x2 - 25((y + 2)2
- 4) + 325 = 0
36x2 - 25(y + 2)2
= -225 |
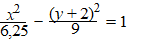 |
Dus a
= 2,5 en b = 3 en de brandpunten liggen op de y-as
en c = √(151/4)
De hyperbool is 2 omlaag geschoven.
De toppen zijn dus (0, 1) en (0, -5)
en de brandpunten (0, -2
± √(151/4)) |
| |
|
| |
|
| 2. |
Geef een vergelijking van de volgende
hyperbolen: |
| |
|
|
|
| |
a. |
Met toppen (-1,1) en (5,1) en brandpunt
(7,1) |
|
16x2 - 64x - 9y2 + 18y - 89 = 0 |
|
| |
b. |
Met top (-2,2) en brandpunten (-2, 6) en
(-2, -4). |
|
x2
- 24y2 + 4x + 48y +
4 = 0 |
|
| |
c. |
Door (6,√5) met
toppen (-4,0) en (4,0). |
|
| |
|
|
|
| 3. |
Geef de brandpunten en toppen van de
volgende hyperbolen: |
| |
|
|
|
| |
a. |
x2 - 7y2
-
14y - 70 = 0 |
|
| |
b. |
16x2 - 9y2
-
32x + 36y + 124 = 0 |
|
(1,6) (1,-2) (1,7) (1,-3) |
|
| |
c. |
x2 - 3y2 + 6x
+ 18 = 0 |
|
| |
d. |
2y2 - x2
- 4y
+ 2x + 5 = 0 |
|
| |
|
|
|
| 4. |
Stel een vergelijking op van de
hyperbool waarvan de richtcirkels de cirkels x2
+ y2 = 16 en (x - 6)2 + y2
= 16 zijn. |
| |
|
|
|
| |
|
|
|
| 5. |
Stel een vergelijking op van de
hyperbool waarvan een richtcirkel (x + 2)2 +
y2 = 25 is en een top (5,0). |
| |
|
|
|
| |
|
|
|
| |
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|