© h.hofstede (h.hofstede@hogeland.nl)

       
Variatie van Parameters.
       
De tweede manier om een particuliere oplossing te vinden was bij tweede orde differentiaalvergelijkingen de methode "Variatie van Parameters".  Lees voor uitgebreidere info daarover eerst deze les door.
Hoe was het ook alweer?  In tegenstelling tot de methode van Onbepaalde Coλfficiλnten werkt deze methode altijd. Het nadeel ervan was dat je soms wel tegen integralen aanloopt die veel te moeilijk zijn om op te lossen.
       

       
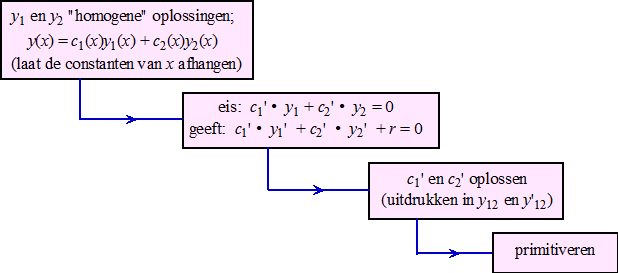
Nou, vooruit dan maar:  hetzelfde voor hogere orde differentiaalvergelijkingen.
Begin met de vergelijking:    y(n) + pn-1 • y(n - 1) + pn-2 • y(n - 2) + ... +  p1 • y' + p0 • y = f(x)  waarbij al die p's en y's van x afhangen.
Stel dat de homogene oplossingen zijn   y1, y2, ... yn 
Probeer als oplossing van de particuliere vergelijking   y = c1 • y1 + c2 • y2 + ... + cn • yn   
Ga er weer van uit dat al die c's ook van x afhangen, en vul deze poging in in de differentiaalvergelijking.

Om die c's op te lossen zul je nu n vergelijkingen nodig hebben. Eens kijken of we die kunnen vinden.  Eventueel door onderweg "handige eisen" te stellen aan de c's.
Als  y = c1 • y1 + c2 • y2 + ... + cn • yn    dan is  y' =  c1' • y1 + c1 • y1' + c2' • y2 +  c2 • y2' + .... +  cn' • yn + cn • yn' 
Kijk dat wordt direct al heel groot, en dat is zelfs nog maar y' .........

Omdat we de c's willen uitrekenen, en om te voorkomen dat het met hogere afgeleiden steeds maar groter zal worden eisen we gewoon direct dat al die termen met c'  gelijk zijn aan nul.

Dus eis gewoon:    c1' • y1 + c2' • y2 + .... +  cn' • yn  = 0
Dan hou je over:    y' =  c1 • y1' + c2 • y2' + .... + cn • yn' 

Met de tweede afgeleide gaan we dan uiteraard precies hetzelfde doen:
  y '' =  c1' • y1' + c1 • y1'' + c2' • y2' +  c2 • y2'' + .... +  cn' • yn' + cn • yn''
eis:    c1' • y1' + c2' • y2' + .... +  cn' • yn'  = 0
geeft:  y '' =  c1 • y1'' + c2 • y2'' + .... + cn • yn''
       
En zo gaan we alsmaar door met hogere en hogere en hogere afgeleiden.  In  het algemeen geeft dat allemaal zulke vergelijkingen:
eis:      c1' • y1(p) + c2' • y2(p) + .... +  cn' • yn(p)  = 0
geeft:     y(p) =  c1 • y1(p)  + c2 • y2(p) + .... + cn • yn(p) 
       
Als die eisen geven samen (n - 1) vergelijkingen voor de c'
Al de vergelijkingen voor y(p)  kun je invullen in de oorspronkelijke differentiaalvergelijking om een nde vergelijking te krijgen. Alleen voor de allerlaatste  y(n)  stel je niet zo'n eis maar laat je de hele vergelijking staan, inclusief de termen met c'

Nou, samen heb je dan n vergelijkingen voor  c1' tot en met cn'  .  Die zul je vast wel op kunnen lossen, dat zal het probleem niet zijn (Overigens krijg je daar weer te maken met de Wronskiaan van de differentiaalvergelijking, dat had je vast al wel verwacht toch?).
Hopelijk kun je daarna die c'  primitiveren om de c te vinden. Dat is een spannender probleem....  
 

Uitgebreid  Voorbeeld.    Los op:    y''' + 2y'' -  y' - 2y  =  1 + et
Karakteristieke vergelijking:   λ3 + 2λ2 - λ - 2 = 0  heeft oplossingen   λ = -1, -2, 1 
De homogene oplossingen zijn dus   e-x  en  e-2x  en  ex
Probeer  y =  ae-x + be-2x + cex    (waarbij  a, b en c ook van x mogen afhangen)

y' = a'e-x - ae-x + b'e-2x - 2be-2x + c'ex + cex
eis:    a'e-x + b'e-2x + c'ex  = 0                                       ........(1)
Dat geeft  y' = -ae-x - 2be-2x + cex

y''  = -a'e-x + ae-x - 2b'e-2x + 4be-2x + c'ex + cex
eis:   -a'e-x - 2b'e-2x + c'ex  = 0                                      .........(2)
Dat geeft:   y''  = ae-x + 4be-2x + cex

y'''  = a'e-x - ae-x + 4b'e-2x - 8be-2x + c'ex + cex            

Vul nu    y,  y' , y''  en y''' in in de oorspronkelijke differentiaalvergelijking:
a'e-x - ae-x + 4b'e-2x-8be-2x + c'ex + cex + 2( ae-x + 4be-2x + cex ) - (-ae-x - 2be-2x + cex ) -2(ae-x + be-2x + cex)=1+ex
rangschikken:
e-x • (a' - a + 2a + a - 2a) + e-2x • (4b' - 8b + 8b + 2b - 2b)  + ex • (c' + c + 2c - c - 2c - 1)  - 1 = 0
a'e-x  + 4b'e-2x   + (c' - 1)ex  =  1                                 ...........(3)

Nu hebben we drie vergelijkingen (1)(2)(3) voor a' en b' en c'.  Die kun je met de regel van Kramer wel oplossen, maar deze drie kunnen ook nog vrij gemakkelijk gewoon door wat substitutie:
  uit (1) volgt  a'e-x = -b'e-2x - c'ex  en dat kun je invullen in (2) en (3):
b'e-2x + c'ex - 2b'e-2x + c'ex  = 0   ofwel  -b'e-2x  + 2c'ex  = 0           .........(2b)
-b'e-2x - c'ex  + 4b'e-2x   + (c' - 1)ex  =  1   ofwel  3b'e-2x  - ex  = 1    .........(3b)
Uit 3b volgt direct  b' = (1 + ex)/3e-2x  =  1/3e2x  + 1/3e-x 
Dan volgt uit  (2b) dat   2c'ex = 1/3 + 1/3ex    dus  c'  = 1/6e-x + 1/6
Dat geeft tenslotte  a'e-x = -1/3 - 1/3ex -  1/6 - 1/6ex   ofwel  a'  =  -1/2ex - 1/2
       
Deze drie primitiveren geeft  a = -1/2ex - 1/2x  en  b =  1/6e2x - 1/3e-x   en   c = -1/6e-x + 1/6x   De eventuele constante bij het primitiveren doet er niet toe, dat zagen we al bij tweede orde vergelijkingen.

Particuliere oplossing:   y =  -1/2 - 1/2xe-x  + 1/6 - 1/3e-3x - 1/6 + 1/6xex
Algemene oplossing:   y =  A • e-x + B • e-2x + C • ex   -1/2 - 1/2xe-x  - 1/3e-3x  + 1/6xex

Voor het vinden van A, B en C heb je beginvoorwaarden nodig.
       

© h.hofstede (h.hofstede@hogeland.nl)