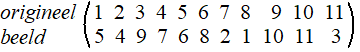definities groep


Algemene Definities Groepen.	© h.hofstede (h.hofstede@hogeland.nl)

Hoogste tijd om na de twee vorige lessen de zaken wat gestructureerder en wiskundig "strenger" te gaan aanpakken.

Een verzameling G met bewerking o is een groep als geldt;
	G1. er is een eenheidselement e. (a o e = e o a = a voor alle a) G2. voor alle a, b en c geldt: a o (b o c) = (a o b) o c G3. voor elke a bestaat er een inverse a^I zodat a o a^I=a^I o a = e

Eigenschap 2 heet de associatieve eigenschap.
Merk nog op dat de commutatieve eigenschap a o b = b o a NIET hoeft te gelden in een groep. Het MAG natuurlijk wel, maar het HOEFT niet! Groepen waarin ook de commutatieve eigenschap geldt, heten Abelse Groepen.

simpel stellinkje 1: bij elke a hoort precies één a^I.
simpel bewijsje 1: stel dat er twee zijn, zodat a^I o a = a o a^I = e en ook a^II o a = a o a^II = e
dan geldt: a^I = a^I o e = a^I o (a o a^II) = (a^I o a) o a^II = e o a^II = a^II.
dus zijn aI en a^II hetzelfde, dis is er maar één a^I.

simpel stellinkje 2: voor de inverse geldt: (a o b)^I = b^I o a^I
sinpel bewijsje 2: (a o b) o (a o b)^I = e
pas aan beide kanten a^I toe: a^I o (a o b) o (a o b)^I = (a^I o a) o b o (a o b)^I = b o (a o b)^I = a^I o e = a^I
pas aan beide kanten b^Itoe: b^I o b o (a o b)^I = (a o b)^I = b^I o a^I
Daarmee is de stelling bewezen.

opmerking: dit wordt ook wel de sokken-en-schoenen regel genoemd. immers als je eerste je sokken aantrekt (b) en daarna je schoenen (a), dan kun je dat proces omkeren door eerst je schoenen uit te trekken (a^I) en daarna je sokken (b^I).

simpel stellinkje 3: er is maar één eenheidselement.
simpel bewijsje 3: stel dat er twee verschillende eenheidselementen e₁ en e₂ zijn.
dan is e₂ o e₁ = e₁ want e₂ is eenheidselement.
dan is e₂ o e₁ = e₂ want e₁ is eenheidselement.
Dus is e₁ = e₂.

Een bijectie is een manier waarop een verzameling V op zichzelf wordt afgebeeld. Niet zo maar een manier.... bij een bijectie wordt elk element van een verzameling op precies één beeldelement afgebeeld. Een bijectie heet daarom ook wel een één-op-één-afbeelding. Bij een bijectie is er een één-op-één-relatie tussen de oorspronkelijke elementen en de beeldelementen.
Zo'n bijectie kun je als een permutatie van V weergeven.

Stelling:

Alle mogelijke bijecties van een verzameling V vormen een groep G
(met de bewerking "na elkaar uitvoeren")

Bewijs:

Twee bijecties na elkaar vormen weer een bijectie (als je eerst de elementen a_i aan b_i koppelt en daarna b_i aan c_i dan koppel je netto gewoon a_i aan c_i.

G1.

Het eenheidselement is natuurlijk de afbeelding waarbij elk element precies op zichzelf wordt afgebeeld.

G2.

"na elkaar uitvoeren" is voor alle afbeeldingen associatief.

G3.

Voor de inverse van een afbeelding "draaien we gewoon alle pijlen om".

Als verzameling V een eindig aantal elementen heeft, dan zijn alle bijecties natuurlijk gewoon samen alle permutaties, immers die geven precies alle mogelijkheden om een verzameling aan zichzelf te koppelen. in dat geval noemen we de verzameling van bijecties S_n; de permutatiegroep.

Cykelnotatie.

Laten we een willekeurige bijectie bekijken, en meteen proberen daar cykels in op te sporen. Hieronder zie je in de bovenste rij het origineel en in de onderste rij het beeld voor een verzameling van 11 elementen.

Wil je dit met cykels opschrijven, dan vind je 1 → 5 → 6 → 8 → 1 en 2 → 4 → 7 → 2 en 3 → 9 → 10 → 11 → 3
Met de cykelnotatie geeft dat (1 5 6 8)(2 4 7)(3 9 10 11).

Stelling:

Elke permutatie is te schrijven als product van losse cykels

Bewijs.

Neem een verzameling X van n elementen x. Stel dat de stelling geldt voor een verzameling met n - 1 of minder elementen (we gaan volledige inductie gebruiken zoals je al wel merkt, en voor een verzameling van één element geldt de stelling zeker).

Kies nu een willekeurige permutatie P.
Als je P herhaaldelijk toepast op een element x, dan krijg je de serie: x, P(x), P²(x), P³(x), ....
Stel dat we in deze rij elementen voor het eerst een dubbele zien staan (eentje die al eerder is geweest) op plaats k. Bijvoorbeeld omdat die ook al op plaats j < k stond....
Dan geldt kennelijk P^j(x) = P^k(x) maar daaruit volgt: P^j • P^-j (x) = P^k • P^-j(x) ofwel x = P^{k - j}(x)
Dat betekent dat op plaats k - j (< k) ook al het element x heeft gestaan. Maar dat kan niet, want k was de eerste dubbele!
De enige mogelijkheid is, dat j = 0 en dat x = P^k(x). Dus het eerste element herhaalt zich op plaats k voor het eerst.

We kunnen de verzameling X nu in twee delen opsplitsen:

•

Het eerste deel: x, P(x), P²(x) , ..., P^k-1(x): dat kunnen we als één cykel schrijven.

•

De "Rest" van verzameling X is een nieuwe verzameling die kleiner dan of gelijk aan n - 1 elementen is, dus volgens de inductieaanname kunnen we ook daarvan een serie losse cykels maken.

De hele verzameling X is dus ook als serie losse cykels te schrijven, namelijk die van het eerste deel plus die anderen van de rest erbij.

q.e.d.

Elke permutatie kan maar op één manier (los van de volgorde) als som van losse cykels geschreven worden. Daarbij kunnen natuurlijk ook heel goed cykels van lengte 1 nodig zijn: dat zijn de punten die op zichzelf worden afgebeeld; ook wel de dekpunten genoemd. De lengtes van die cykels samen zijn dan uiteraard precies gelijk aan het aantal elementen van de verzameling. In het voorbeeld hierboven hebben we een verzameling van 11 elementen, met cykels van lengte 4, 3 en 4; samen precies 11. Zo'n "opdeling" van 11 in kleinere getallen heet ook wel een partitie. Het rijtje getallen 4 - 3 - 4 heet ook wel het cykeltype.

De orde van een groep en de orde van een element.

De orde van een groep is gewoon gelijk aan het aantal elementen van die groep. Een groep met oneindig veel elementen heeft dus orde oneindig.
De orde van een element van een groep hebben we al gehad: het is het kleinste getal n waarvoor geldt aⁿ = e. Zeg maar "hoe vaak je het element moet doen om e te krijgen". Dat betekent dat in de rij a, a², a³, ... bij aⁿ voor het eerst e staat. En vanaf die n gaat de rij zich dus herhalen, immers aⁿ⁺¹= aⁿ • a = e • a = a, en zo is aⁿ⁺² = a² enz.
Grappig: in zo'n geval is a^{n - 1} dus de inverse (a^I) van a; kijk maar: a^{n - 1} • a = aⁿ = e

OPGAVEN

1.	Hieronder staan twee cykelrepresentaties van een bijectie van een verzameling met acht elementen. Deze cykels zijn echter niet disjunct (ze "overlappen"). Niet-genoemde elementen worden gewoon op zichzelf afgebeeld. Schrijf deze bijecties in de vorm van wél disjuncte cykels.

	a.	(2 4 5 6)(8 6 4)(1 7 8)

	b.	(1 3 4)(2 3 5 6 7)(5 6 7 8)