| |
 |
| sina
= sinb |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
Nou ja, wat een stomme
vergelijking" zul je wel denken. "Ik zie natuurlijk meteen de
oplossing: a = b Dûh!!"
Maar dan vergeet je toch iets!
Om precies te zijn: Je vergeet TWEE dingen!!
En dat zijn dezelfde twee dingen die we al tegenkwamen bij het oplossen
van sinx = p |
|
|
De oplossing moet + k
2π
Er is een tweede oplossing:
π
- eerste |
|
|
|
En bij cosa = cosb
gebeurt precies hetzelfde, alleen is dan de tweede oplossing 2π
- eerste.
Denk erom dat in plaats van de a en b van alles mag staan.
Dus, samengevat: |
|
|
|
|
sin a = sin b
⇒ a = b + k
2π
∨
a =
π
- b + k
2π
cosa = cosb ⇒
a = b + k 2π
∨ a = 2π
- b + k 2π |
|
| |
|
| Voorbeeld:
Los op in [0, 2π]:
sin(2x + 1/3π)
= sin(x) |
|
In dit geval is a = 2x +
1/3π
en b = x
Dat geeft dus: 2x + 1/3π
= x + k 2π ∨ 2x
+ 1/3π
=
π - x + k 2π
⇒ x = -1/3π
+ k 2π ∨ 3x =
2/3π
+ k 2π
⇒ x = -1/3π
+ k 2π ∨ x =
2/9π
+ k 2/3π
Dat geeft tussen 0 en 2π de
oplossingen: x = 2/9π,
x = 8/9π,
x = 15/9π,
x = 12/3π |
|
|
| 1. |
Los op in [0,2π]:
|
|
a. |
sin(x - 1/6π)
= sinx |
e. |
sin(x + 1/4π)
= sin(3x - 1/3π) |
|
b. |
cos(x) = cos(x + 1/4π) |
f. |
sin(1/2x)
= sin(π
- x) |
|
|
c. |
cos(2x) = cos(x + 1) |
g. |
sin(x + 4) = sin(2 - x) |
|
|
d. |
cos(x +
π) -
cos2x = 0 |
h. |
cos(2x + 2/3π)
= cos(1/6π
- x) |
|
|
|
|
|
|
| 2. |
De vergelijking sin(x) = sin(x +
p) heeft als oplossing o.a. x = 1/6π.
Bereken drie mogelijke waarden voor p. |
| |
|
|
|
|
|
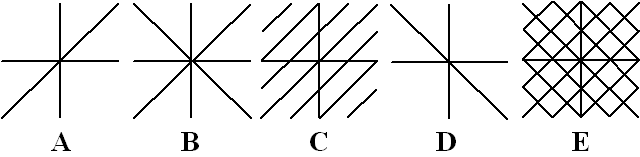
| 3. |
Olympiadevraagstuk.
In welk van onderstaande figuren zijn de punten getekend waarvoor
geldt cosx = cosy ? |
| |
|
|
|
|
|
| |
 |
| |
|
|
|
|
|
| 4. |
Teken de verzameling van alle punten
(x, y) waarvoor geldt: sinx
≥ siny.
Neem x en y beiden in [0, 2π] |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |