© h.hofstede (h.hofstede@hogeland.nl)

Getaltheorie.

Het zal je wel niet erg verbazen dat getaltheorie de theorie van getallen behandelt.......
In deze inleiding daarom eerst maar wat afspraken en namen over getallen.

Verzamelingen.
       

De verzameling van de natuurlijke getallen is de verzameling  ℕ = {0, 1, 2, 3, 4...}
       
Je ziet dat er voor verzamelingen hoofdletters met een dubbele poot worden gebruikt.
Die verzameling ℕ heeft één heel belangrijke eigenschap, en dat is het welordeningsprincipe, en dat luidt als volgt:
       

Elke niet-lege deelverzameling van ℕ heeft een kleinste element.
       
Dit principe maakt het mogelijk om de natuurlijke getallen te rangschikken van klein naar groot, immers als je van elke groep weet wat de kleinste is, kun je ze ook op volgorde zetten.

inductieprincipe.
Het welordeningsprincipe legt de basis voor een bewijssoort die "volledige inductie" wordt genoemd, namelijk op de volgende manier.
Stel dat U(n) een uitspraak is, waarvan het WAAR of ONWAAR zijn afhangt van de waarde van een natuurlijk getal n.
Bijvoorbeeld:  
U(n) = "n < 6"  is WAAR voor n = 0, 1, 2, 3, 4, 5 en ONWAAR voor alle anderen natuurlijke getallen
U(n) = " n is een priemgetal"  is WAAR voor n = 7  en ONWAAR voor n = 9.

Het inductieprincipe zegt dan:
"Als U(0) WAAR is, en als verder voor elke k ∈ ℕ volgt dat, als U(k) WAAR is, dat dan ook  U(k + 1) WAAR is, dan is U(n) WAAR voor alle n".

Bewijs.
  Stel dat U(0) WAAR is, en dat uit het WAAR zijn van U(k) volgt dat U(k + 1) WAAR is.

Stel nu dat er een U(n) is die ONWAAR is......
Noem de verzameling van natuurlijke getallen waarvoor U(n) ONWAAR is de verzameling V. Dan is V dus niet leeg.
Volgens het welordeningsprincipe heeft V dus een kleinste element k.  Maar we weten dat  k ≠ 0 want U(0) was WAAR.
Omdat k > 0  is  k - 1 ook een natuurlijk getal, en daarvoor is  U(k -1) WAAR, want k - 1 is kleiner dan k en k was het kleinste element van V.
Maar uit het WAAR zijn van U(k - 1)  volgt dat  U((k - 1) + 1) óók WAAR is, dus dat U(k) WAAR is.
Dit is een tegenstrijdigheid,  dus er is geen n waarvoor U(n) ONWAAR is.
q.e.d.    
       
Genoeg over het inductieprincipe, als je er meer over wilt weten moet je deze les maar bekijken.
Op naar de volgende verzameling:
       

De verzameling van de gehele getallen is de verzameling  ℤ  = {..., -2, -1, 0, 1, 2, ...}
       
Het is eigenlijk de verzameling van alle mogelijke verschillen van natuurlijke getallen.
Op naar de volgende:
       

De verzameling van de rationale getallen is de verzameling  ℚ
die bestaat uit alle getallen die geschreven kunnen worden als a/b
waarbij a en b natuurlijke getallen zijn en b ≠ 0
       
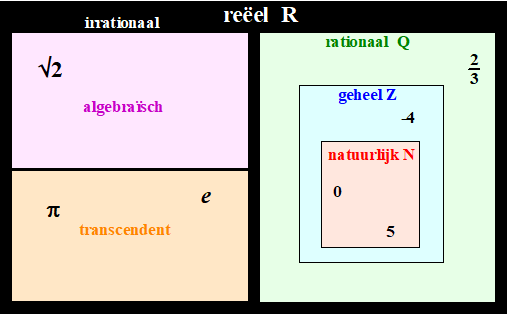
Het is eigenlijk de verzameling van alle mogelijke quotiënten van natuurlijke getallen. Ofwel:  het zijn alle breuken.

Getallen die niet rationaal zijn, noemen we irrationale getallen. Het zijn eigenlijk de getallen die de gaten opvullen, die de rationale getallen op de getallenlijn achterlaten. Irrationale getallen zijn niet als breuk te schrijven, maar wel als limiet van een rij van rationale getallen.
De irrationale en rationale getallen samen noemen we de reële getallen en die geven we aan met de letter ℝ. Omdat irrationale getallen als limiet van een rij breuken kunnen worden weergegeven wordt de verzameling ℝ wel de Cauchy-completering van ℚ genoemd.

De irrationale getallen kunnen nog worden ingedeeld in twee categorieën, namelijk de transcendente getallen en de algebraïsche getallen.
Transcendente getallen zijn getallen die NIET het nulpunt zijn van een polynoom met rationale coëfficiënten en eindige graad.
Dat betekent dus dat, als x een transcendent getal is, er GEEN vergelijking te vinden is van de vorm  a0 + a1x + a2x2 + .... + anxn = 0   met  a's  allemaal rationaal zodat x een oplossing is. Voor algebraïsche getallen is er altijd WEL zo'n vergelijking te vinden.
Transcendente getallen kun je ook NIET met een passer en een liniaal op de getallenlijn construeren. Beroemde transcendente getallen zijn  bijvoorbeeld  π en e.

Het volgende diagram vat al die getallenverzamelingen goed samen:
       

       
De eerlijkheid gebied me te zeggen dat je er nog een rechthoek omheen zou kunnen tekenen met de Complexe getallen. Maar die getallen komen in deze lessen over getaltheorie nauwelijks voor.

Er is nog iets op te merken over de begrenzing van een verzameling.
•  een verzameling V is naar boven begrensd als er een getal bestaat dat minstens zo groot is als elk getal uit V.
•  een verzameling V is naar onderen begrensd als er een getal bestaat dat hoogstens zo groot is als elk getal uit V.

Een naar boven begrensde verzameling hoeft niet noodzakelijk een maximum te hebben. Neem het interval  [0, 1〉.
Maar wel geldt de volgende eigenschap; het zogenaamde supremumprincipe over ℝ:
       

Een niet-lege deelverzameling V van ℝ, die naar boven begrensd is,
heeft een  kleinste bovengrens
       
Die kleinste bovengrens heet het supremum, en wordt genoteerd als  sup(V).
En analoog hieraan heeft elke niet-lege deelverzameling V van ℝ die naar onderen is begrensd een grootste ondergrens; het infimum, genoteerd als inf(V).
       
Afronden en Afkappen.

Met al die begrenzingen en grootste en kleinste onder- en bovengrenzen  zijn een paar nieuwe begrippen te maken.
Kom, we gooien er eerst een definitie voor het afkappen van een getal tegenaan:
       
⌊r⌋  is het grootste gehele getal dat kleiner of gelijk aan r is. 
       
Het wordt ook wel  "floor-r" genoemd, en is natuurlijk eigenlijk niets anders dan het gehele deel van r. Ofwel het gedeelte vóór de komma.
De functie   f(r) = ⌊r⌋  heet (behalve de floor-functie)ook wel de "Entierfunctie" of de "Integerfunctie".

Natuurlijk is er ook een naam voor het gedeelte achter de komma van een getal r :
       

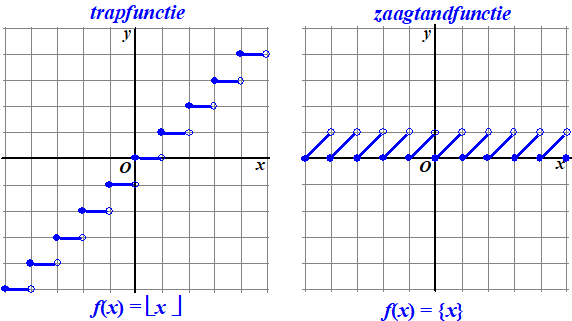
Het fractionele deel van een  getal  r  is gelijk aan  {r} =  ⌊r⌋  - r 

       
Bedenk dus dat  {4} = 0  en  {3,8} = 0,8  en  {-4,3} = 0,7.
Hieronder zie je de grafieken van  f(x) = ⌊r⌋   en  f(x) = {x}. Kijk ernaar en je zult snappen dat ze ook wel de "trapfunctie" en de "zaagtandfunctie" worden genoemd.
       

       
Naar boven afronden kan ook:  ⌈r⌉ is het kleinste gehele getal, groter of gelijk aan r.  We noemen het ook wel  "ceil-r" en de functie  f(x) = ⌈x⌉ heet ook wel de  ceiling-functie. Het is natuurlijk niets anders dan  "naar boven afronden" en de grafiek is weer zo'n trapfunctie (met alle treden net eentje hoger).
       
       
   OPGAVEN
       
1. Onderzoek  hoe groot  ⌊2x⌋ - 2⌊x⌋  kan zijn.
     

   0 of 1
       
     
       
       

© h.hofstede (h.hofstede@hogeland.nl)