verdelingen vergelijken

© h.hofstede (h.hofstede@hogeland.nl)

Gemengde opgaven.

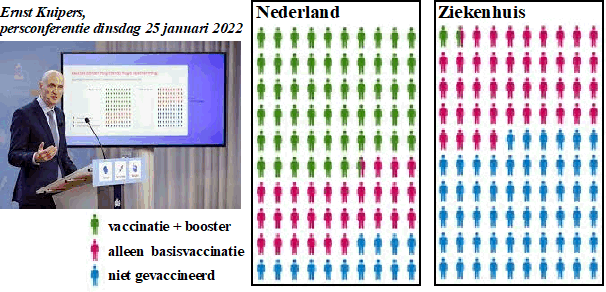
Hierboven zie je minister Kuipers van volksgezondheid op de corona-persconferentie van dinsdag 25 januari 2022. Hij laat hier twee diagrammen zien die rechts vergroot staan weergegeven.

Het linkerdiagram geeft aan hoeveel van de mensen in Nederland een boostervaccinatie hebben of alleen een basisvaccinatie of niet gevaccineerd zijn. Het rechterdiagram geeft deze aantallen voor de mensen die vanwege corona in het ziekenhuis liggen.

Neem aan dat Nederland 17440000 inwoners heeft en dat er op 25 januari 1028 mensen vanwege corona in een ziekenhuis lagen.

Bereken met deze gegevens hoeveel procent van de mensen met een boostervaccinatie in het ziekenhuis liggen en hoeveel procent van de ongevaccineerden in het ziekenhuis liggen.
Hoeveel keer zo groot is de kans om in het ziekenhuis te komen voor een ongevaccineerde vergeleken met iemand met een boosterprik?

160 keer

Wilma Appie gelooft de cijfers van Kuipers niet. Zij leest af dat ongeveer 56% van de mensen in het ziekenhuis ongevaccineerden zijn, en denkt dat dat een veel te hoog aantal is.
Wilma belt met het UMCG in Groningen en krijgt van hen te horen dat er bij hen 22 coronagevallen liggen waarvan 11 ongevaccineerd.
"Zie je wel: 50%! Die 56% is gewoon keihard gelogen" roept Wilma woedend en ze gaat uiteraard direct een demonstratie organiseren.

Bereken welk 95%-betrouwbaarheidsinterval Wilma op grond van de gegevens uit Groningen mag opstellen voor de proportie ongevaccineerden in het ziekenhuis in Nederland

[0.304 ; 0.696]

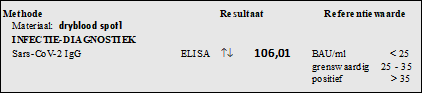
Na een vaccinatie heb je antistoffen in je bloed. De zogenaamde "spike-antistoffen Sars-Cov-2".
De Euroimmun-test meet door een vingerprik de hoeveelheid van deze antistoffen in je bloed. Hieronder zie je de uitslag van zo'n test.

Deze uitslag was een waarde van 106,01.
Je ziet rechts dat waarden boven de 35 positief zijn, en tussen de 25 - 35 grensgevallen

Als na de eerste prik het aantal antistoffen normaal verdeeld is met een gemiddelde van 45 en een standaardafwijking van 10, hoeveel procent van die mensen zal dan na 3 dagen een positief resultaat hebben?

84%

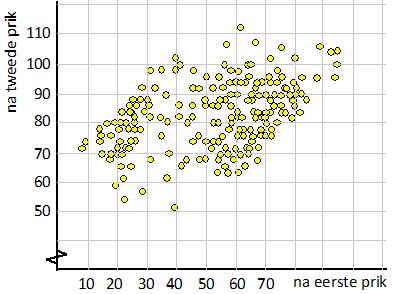
Een groot aantal mensen die met Astra-Zeneca zijn gevaccineerd heeft op verzoek van de GGD 3 dagen na hun eerste prik en ook 3 dagen na hun tweede prik de hoeveelheid antistoffen in hun bloed gemeten. Dat leverde het volgende spreidingsdiagram op:

Leg uit hoe je aan dit diagram kunt zien dat de hoeveelheden antistoffen 3 dagen na de eerste prik niet normaal verdeeld zijn

Geef in de figuur op het werkblad aan bij welke mensen het aantal antistoffen 3 dagen na de tweede prik meer dan dubbel zo groot was als 3 dagen na de eerste prik.

Stappenteller

Twee groepen van 1000 HBO-studenten en 1000 Universiteits-studenten is gevraagd om een poos een stappenteller te dragen en bij te houden hoeveel stappen er gemiddeld per dag werden gezet.
Dat leverde de volgende tabel op:

gemiddeld aantal stappen per dag	HBO	Universiteit
2000 -< 4000	42	71
4000 -< 6000	96	243
6000 -< 8000	144	346
8000 -< 10000	251	102
10000 -< 12000	332	81
12000 -< 14000	103	60
14000 -< 16000	22	47
16000 -< 18000	10	50

Het gemiddelde van de HBO-studenten is ongeveer gelijk aan 9400 stappen en de standaardafwijking is 2800 stappen.
Je zou deze twee getallen nauwkeuriger kunnen berekenen.

Bereken deze twee getallen nauwkeuriger

9364 en 2811

Leg duidelijk uit waarom zo'n nauwkeuriger berekening niet zinvol is.

Bereken het 95%-betrouwbaarheidsinterval van het gemiddelde aantal stappen van de HBO-studenten.

[9223; 9577]

Bereken met het Max Vcp of het verschil in stappen tussen deze twee groepen gering, middelmatig of groot is.

37,8%, middel

Nijmeegse vierdaagse.

De Nijmeegse Vierdaagse, officieel de Internationale Vierdaagse Afstandsmarsen Nijmegen, is een vierdaags wandelevenement dat sinds 1909 ieder jaar wordt gehouden en start op de derde dinsdag van juli. De Nijmeegse Wandelvierdaagse is de oudste en meest bekende Vierdaagse in Nederland. Het is de grootste meerdaagse wandelprestatietocht ter wereld en staat inmiddels ook bekend als The Walk of the World. Elk jaar doen er deelnemers uit circa tachtig landen mee, onder wie een groot aantal militairen. De aantallen deelnemers in 2019 zie je in de volgende tabel.

	Nederland			Andere Landen
	gemiddelde leeftijd	standaard afwijking	aantal deelnemers	gemiddelde leeftijd	standaard afwijking	aantal deelnemers
Militair	32,0	6,0	4320	39,9	5,1	1182
Niet-Militair	44,5	12,3	31645	41,6	10,1	8737

Bereken of het verschil in aantallen militairen en niet-militairen die deelnemen tussen Nederland en de Andere Landen groot, middelmatig of gemiddeld is.

Bereken de gemiddelde leeftijd van alle deelnemers.

Neem aan dat de leeftijden van de deelnemende Nederlandse militairen normaal verdeeld waren.

Bereken hoeveel deelnemende Nederlandse militairen dan een leeftijd tussen de 26 en 44 jaar hadden.

Bereken of Is het verschil tussen de leeftijden van de militairen van Nederland en de militairen uit de Andere Landen groot, klein of middelmatig is.

Aantallen auto's

De laatste jaren komen er meer en meer elektrische auto’s in Nederland. Onderstaand diagram geeft aan welk deel van alle personenauto’s in Nederland benzineauto of dieselauto of elektrische auto is.

Een onderzoeker wil gaan controleren of de gegevens inderdaad wel kloppen. Zo ziet hij in het diagram dat 9% van de auto’s elektrisch is.
Hij meet daarom een week lang 8 uur per dag hoeveel elektrische auto’s er op een bepaald kruispunt voorbijkomen, en ook hoeveel auto's er in totaal langskomen
Van de totaal 1568 blijken er 131 elektrisch te zijn.

Geef aan de hand van deze metingen een 95%-betrouwbaarheidsinterval voor het percentage elektrische auto’s in Nederland. Geef je getallen in drie decimalen nauwkeurig.

Wat is er niet goed aan de steekproef die de onderzoeker heeft genomen?

In totaal waren er in 2021 ongeveer 8,8 miljoen personenauto’s in Nederland. Daarvan waren er ongeveer 6500 bij een ongeluk betrokken. In onderstaande figuur zie je hoe die 6500 auto’s verdeeld waren over benzineauto’s en dieselauto’s en elektrische auto’s.

Bereken met behulp van bovenstaande gegevens hoeveel procent van de elektrische auto’s in 2021 betrokken was bij een ongeluk.

Het percentage benzineauto’s dat bij een ongeluk was betrokken was ongeveer 0,05%. Er is een theorie dat elektrische auto’s vaker bij een ongeluk zijn betrokken omdat ze minder lawaai maken. Dat heeft tot gevolg dat bijvoorbeeld fietsers deze auto’s minder goed horen aankomen.

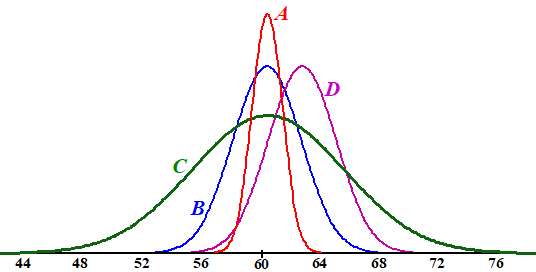
Het geluidsniveau wordt uitgedrukt in aantal Decibel (dB)

Meting onder een aantal elektrische auto’s leverde op dat ze op 2 meter afstand een geluidniveau van 60,2 dB leveren met een standaardafwijking van 2,3 dB. Benzineauto’s geven 63,8 dB geluidsniveau met een standaardafwijking van 2,9 dB

Hieronder staan vier mogelijke normale verdelingen.

Welk van deze vier verdelingen zou kunnen horen bij het geluidsniveau van elektrische auto's? Geef een duidelijk uitleg.

In de tabel hieronder staan de metingen van het geluidsniveau op 2 meter afstand van 20 dieselautos

60	65	61	64	62	65	66	61	59	65
64	66	66	62	63	67	67	65	64	62

Het gemiddelde blijkt gelijk te zijn aan 63,7 en de standaardafwijking is ongeveer 2,3.

Bereken deze standaardafwijking in drie decimalen nauwkeurig

Geef aan de hand van deze gegevens een 95%-betrouwbaarheidsinterval voor het geluidsniveau van dieselautos.

Gemiddelde dagtemperatuur.

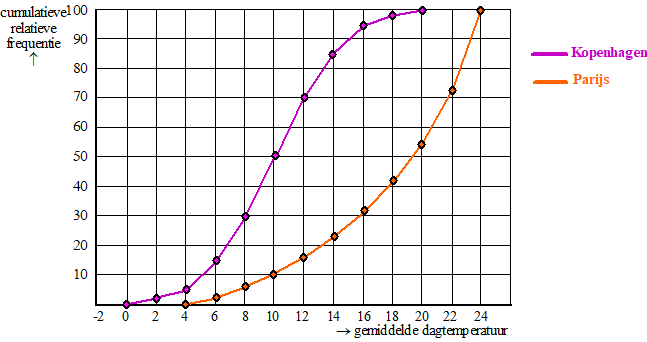
Een aantal dagen is de gemiddelde dagtemperatuur gemeten in de steden Parijs en Kopenhagen.

Hieronder zie je van de resultaten daarvan in één figuur twee relatieve cumulatieve frequentiepolygonen.

Eén van beiden hoort bij een normale verdeling.

Leg duidelijk uit welk van beiden bij een normale verdeling hoort, en geef ook aan hoe de verdeling van de andere wordt genoemd.

Bepaal het MaxV_cp van deze verdelingen en leg daarmee uit of het verschil tussen de temperaturen in deze twee steden groot, middelmatig of klein is.

Bepaal met boxplots of het verschil tussen de temperaturen in de twee steden groot, middelmatig of klein is.

Examenopgave HAVO Wiskunde A, 2022-I

In veel dorpen geldt een snelheidslimiet van 30 of 50 km/uur. Niet elke automobilist houdt zich hieraan en dit kan onveilige situaties opleveren. Daarom kan iedereen onveilige verkeerssituaties melden bij Veilig Verkeer Nederland (VVN). Als men bij VVN het vermoeden heeft dat het om een gegronde melding gaat, dan gaan vrijwilligers op pad om de snelheid van passerende automobilisten te meten.

Vanuit het dorp Borssele is zo’n melding binnengekomen over de Monsterweg. Vervolgens is op een dinsdagochtend tussen 7 en 9 uur op deze weg de snelheid van 250 passerende automobilisten gemeten. Aan de hand van de resultaten van deze steekproef wil men een uitspraak doen over het percentage automobilisten dat in een willekeurige week op deze weg te hard rijdt.

Leg uit waarom deze steekproef waarschijnlijk niet representatief is en geef aan hoe dat verbeterd kan worden.

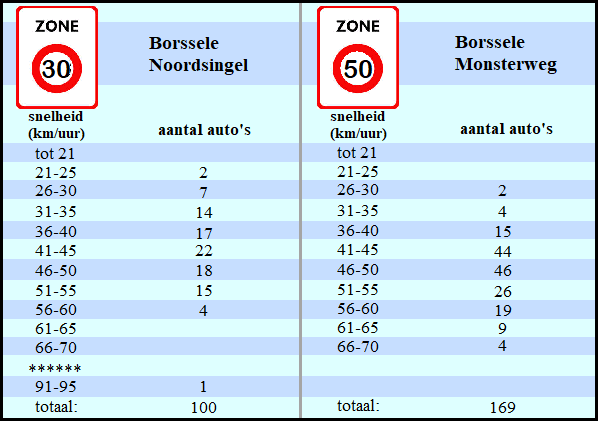
Er wordt een nieuwe steekproef op de Monsterweg gehouden die wel representatief is. Op deze weg, waar de snelheidslimiet 50 km/uur is, is de snelheid van 169 auto’s gemeten.
Ook wordt er een representatieve steekproef gehouden op de Noordsingel in Borssele. Op deze weg, waar de snelheidslimiet 30 km/uur is, is de snelheid van 100 auto’s gemeten. De resultaten van de twee steekproeven zijn weergegeven in de figuur.

Ligt de snelheidslimiet op de Noordsingel in de modale klasse? Licht je antwoord toe.

De situatie op de Noordsingel is zorgwekkend: er waren maar weinig automobilisten die zich aan de snelheidslimiet hielden. Men wil het 95%-betrouwbaarheidsinterval berekenen van het percentage automobilisten op de Noordsingel dat te hard rijdt.

Bereken dit 95%-betrouwbaarheidsinterval. Rond de percentages in je antwoord af op gehele getallen.

Piet wil een diagram maken met de gegevens van de Monsterweg uit de figuur. Hij overweegt de volgende drie diagrammen:
- een boxplot
- een spreidingsdiagram (puntenwolk)
- een cumulatieve relatieve frequentiepolygoon

Hij wil dat uit het diagram af te lezen is hoe groot het percentage van de automobilisten is dat zich aan de snelheidslimiet houdt.

Geef voor elk van deze drie diagrammen aan of dat hiervoor geschikt is. Licht je antwoord telkens toe.

Voor de Monsterweg wordt onderzocht of een groter deel van de automobilisten zich aan de snelheidslimiet houdt als er matrixborden langs de weg worden geplaatst die de maximumsnelheid aangeven. Zie de foto.

In het eerdere onderzoek (situatie zonder matrixborden) van VVN hielden 111 van de 169 automobilisten op de Monsterweg zich aan de snelheidslimiet. In het vervolgonderzoek, waarin er matrixborden geplaatst waren, hielden 183 van de 213 automobilisten zich aan de snelheidslimiet. In de twee onderzoeken is het deel van de automobilisten dat zich aan de snelheidslimiet houdt dus verschillend.

Bepaal met behulp van het formuleblad of dit verschil gering, middelmatig of groot is.

Drankgebruik in de Lage Landen.

Gegevens over het gemiddeld aantal gedronken glazen bier per week van Nederlandse en Belgische volwassenen leverde de volgende tabel:

Glazen per week	0	1	2	3	4	5	6	7	8
BELGIË	40	52	83	121	200	354	403	202	158
NEDERLAND	31	32	44	46	65	88	100	105	109

Glazen per week	9	10	11	12	13	14	15	16	17
BELGIË	100	94	92	76	70	64	64	57	42
NEDERLAND	214	326	450	302	225	145	120	60	24

Glazen per week	18	19	20	21	22	23	24	25
BELGIË	22	20	18	17	10	8	8	4
NEDERLAND	18	14	12	12	12	9	5	1

Iemand wordt als alcoholist beschouwd als hij gemiddeld meer dan 15 glazen bier per week drinkt.
Neem aan dat de standaardafwijking in de gehele populaties steeds gelijk is aan de standaardafwijking in deze steekproeven.

Bereken met het maxV_cp of het verschil tussen België en Nederland gering, middelmatig of groot is.

Bereken met de effectgrootte of het verschil tussen België en Nederland gering, middelmatig of groot is.

Bereken met boxplots of het verschil tussen België en Nederland gering, middelmatig of groot is.

Bereken met de phi-coëfficiënt of het verschil tussen het aantal alcoholisten in België en Nederland gering, middelmatig of groot is.