 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
Gemengde opgaven, parameterkrommen. |
|
|
| 1. |
Kromme K hiernaast
wordt gegeven door:
x(t) = 1/2
- 1/2cos(2t)
en y(t) = 2/3sin3t
|
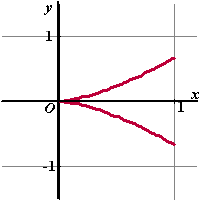 |
| |
|
|
| |
a. |
Stel een formule op voor de baansnelheid van
punt P als functie van t en bereken daarmee de lengte van deze
kromme. |
| |
|
|
| |
Deze kromme is een deel van de
grafiek van y = ±
2/3x√x |
| |
|
|
| |
b. |
Toon dat aan. |
| |
|
|
| |
c. |
Bereken met deze formule opnieuw, nu
algebraïsch, de lengte van de kromme. |
| |
|
|
|
| 2. |
Gegeven zijn de parameterkrommen Ka
door x(t) = t3 - at
en y(t) = t2 en
a > 0 |
| |
Die krommen hebben
allemaal een vorm zoals hiernaast geschetst.
Het snijpunt met de positieve y-as is het punt (0, a) |
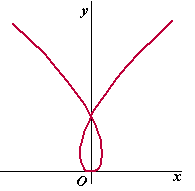 |
| |
|
|
| |
a. |
Toon dat aan. |
| |
|
|
| |
b. |
Onderzoek of het punt waar de snelheid van P
minimaal is samenvalt met een punt waar de raaklijn evenwijdig aan de
y-as is. |
| |
|
|
| |
c. |
Neem a = 2 en bereken de
lengte van alleen het lusje in twee decimalen nauwkeurig |
| |
|
|
|
| 3. |
Een "Tricuspoïde"
ziet eruit als hiernaast.
De vergelijkingen zijn x(t) = 2cost + cos(2t)
en y = 2sint - sin(2t) |
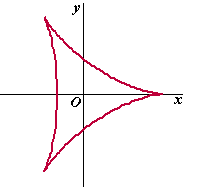 |
| |
|
|
| |
a. |
Bereken de coördinaten van de snijpunten van K
met de coördinaatassen. |
| |
|
|
| |
b. |
Geef een vergelijking van de raaklijn in het
punt waar t = 1/4π |
| |
|
|
| |
Voor de snelheid van
punt P geldt v = √(8 - 8sint) |
| |
|
|
|

|
c. |
Toon dat aan. |
| |
|
|
| |
d. |
Bereken de lengte van de tricuspoïde |
| |
|
|
|
| 4. |
Gegeven zijn de parameterkrommen Ka
door: x(t) = sin(t + a) en
y(t) = cost + cos(3t)
Hieronder zie je voor een aantal waarden van a de kromme Ka |
| |
|
|
|
| |
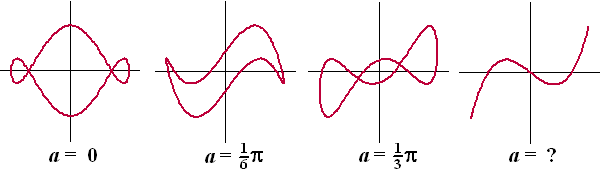 |
| |
|
|
|
| |
a. |
Onderzoek welke waarde van a bij de vierde kromme
hoort. |
| |
|
|
| |
b. |
Toon aan dat de kromme met
a = -1/2π
ook te schrijven is als y = 2x - 4x3 |
| |
|
|
| |
c. |
De kromme met a =
1/3π
heeft twee snijpunten met de y-as. Bereken de afstand tussen die
snijpunten. |
| |
|
|
| |
d. |
De kromme met a =
1/6π
lijkt een keerpunt te hebben voor t = 1/3π.
Onderzoek algebraïsch of dat inderdaad zo is. |
| |
|
|
|
| 5. |
De krommen met x(t)
= sint en y(t) = 2sin(t
- aπ)
zijn allemaal ellipsen: |
| |
|
|
|
| |
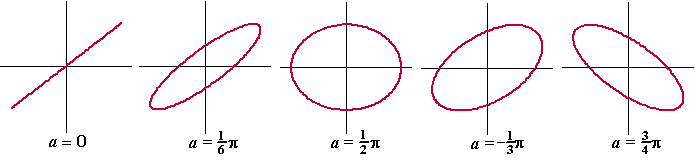 |
| |
|
|
|
| |
Als a =
1/2
kun je de snelheid van punt P beschrijven door v =
√(1 + 3sin2t) |
| |
|
|
|
| |
a. |
Toon aan dat dat zo is. |
| |
|
|
| |
b. |
Bereken de omtrek van de ellips
met a = 1/2π |
| |
|
|
|
| |
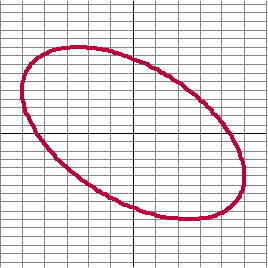
c. |
Bepaal zo nauwkeurig mogelijk de waarde van
a die bij de ellips hiernaast hoort. Geef een duidelijke uitleg
van je werkwijze. |
 |
| |
|
|
|
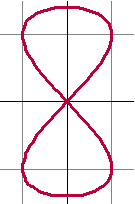
| 6. |
Hiernaast zie je de kromme K
gegeven door: |
 |
| |
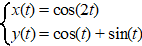 |
| |
|
|
| |
a. |
Bereken in graden nauwkeurig de hoek waaronder
K zichzelf snijdt. |
| |
|
|
| |
b. |
Toon aan dat elk punt van K voldoet aan x2
+ (y2 - 1)2 = 1 |
| |
|
|
| |
c. |
P is een punt van K. Bereken de maximale
waarde van OP. |
| |
|
|
|
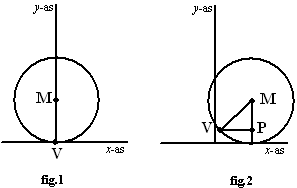
| 7. |
Een
wiel met straal 1 meter rust op de x-as met het ventiel V in de
oorsprong. Het wiel gaat rollen over de x-as waarbij het in 2π
seconden precies één omwenteling voltooit. We bekijken de beweging die
punt V aflegt.
Draait het wiel over een hoek van t radialen (in t
seconden dus) dan is de situatie als in figuur 2, met ∠VMP
= t. Punt M is dan over een afstand t horizontaal
verplaatst. |
 |
| |
|
|
| |
a. |
Bewijs
dat MP = cost en dat
VP = sint
Laat vervolgens zien dat de coördinaten van V voldoen aan:
x(t) = t - sint en y(t) = 1
- cos t
Plot
de grafiek van deze parameterkromme (neem t > 0) |
| |
|
|
|
| |
b. |
Tussen
t = 0 en t = 2π bevindt V zich tweemaal op hoogte
0,5.
Bereken de afstand tussen de twee punten waarvoor dat zo is. |
| |
|
|
|
| |
c. |
Bereken
wanneer punt V een snelheid van 1
m/s heeft. |
| |
|
|
|
| |
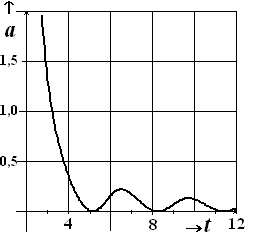
 d. d. |
Vanaf een
willekeurige plaats van punt
V trekken we een lijn naar de oorsprong. Deze lijn heeft vergelijking y
= ax.
De waarde van a hangt dus af van de plaats van punt V, dus ook
van de tijd t.
De grafiek van a als functie van t staat hiernaast
geschetst.
Geef een functievoorschrift voor deze functie. |
 |
| |
|
|
|
| 8. |
examenvraagstuk
VWO Wiskunde B, 1997. |
| |
|
|
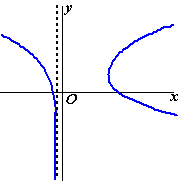 |
| |
De kromme K die in
de figuur hiernaast is getekend, is gegeven door: |
| |
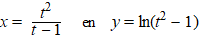 |
| |
waarbij t
∈ 〈←, -1〉
∪
〈1, →〉
|
| |
|
|
| |
a. |
Bereken de coördinaten van de
punt(en) van K waar de raaklijn aan K evenwijdig is aan de y-as. |
| |
|
|
|
| |
Er is een waarde
van p ∈ R zo dat de lijn y
= x + p de kromme K raakt. |
| |
|
|
|
| |
b. |
Bereken p. |
| |
|
|
|
| |
Voor elke a
∈ R snijdt de lijn y = a
de kromme K in de punten Pa en Qa.
Ma is het midden van lijnstuk PaQa. |
| |
|
|
|
| |
c. |
Toon aan dat de
x-coördinaat van Ma gelijk is aan 1 + e-a |
| |
|
|
|
| 9. |
examenvraagstuk
VWO Wiskunde B, 2006. |
| |
|
|
|
| |
De plaats van een bewegend punt
P in een assenstelsel wordt gegeven door:
x(t) = cos2t en y(t) = cos3t,
waarbij t de tijd voorstelt,
met 0 ≤ t
≤
π.
De baan van het punt P lijkt op de Griekse letter
α.
Zie de figuur.Op het tijdstip t
= 0 bevindt P zich in (1,1), dus even ver van de x-as als van de y-as. |
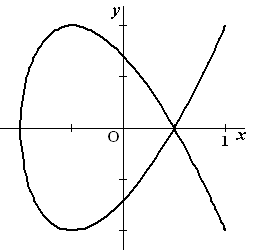 |
| |
|
|
| |
a. |
Bereken het eerste tijdstip na t = 0
waarop P zich wéér even ver van de x-as als van de y-as
bevindt. |
| |
|
|
|
| |
Tussen t = 0 en t
=
π beweegt P éénmaal over de baan.
Gedurende twee tijdsintervallen bevindt P zich boven de lijn y
= 1/2. |
| |
|
|
|
| |
b. |
Bereken de totale tijd dat P zich boven de lijn y =
1/2 bevindt. |
| |
|
|
|
| |
c. |
Onderzoek of de grootste snelheid van het punt P wordt
bereikt op het tijdstip t = 1/2π. |
| |
|
|
|
| |
|
|
|
| 10. |
examenvraagstuk
VWO Wiskunde B, 2012.
Punt
P
doorloopt in het
Oxy-vlak
een ellipsvormige baan volgens de bewegingsvergelijkingen |
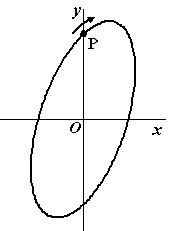 |
| |
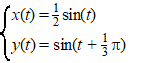 |
| |
Hierin is t de tijd.
De baan van P is gegeven in de figuur hiernaast
Gedurende de beweging verandert de afstand van
P
tot de oorsprong. |
| |
|
|
|
| |
a. |
Bereken de maximale afstand van
P
tot de oorsprong. Geef je antwoord
in twee decimalen nauwkeurig. |
| |
|
|
|
| |
b. |
Bereken exact de snelheid van P
als
t
=
0
. |
| |
|
|
|
| |
c. |
De baan van P
snijdt de lijn met
vergelijking y
=
2x
in de punten
A
en
B.
Bereken exact de coördinaten van A en B. |
| |
|
|
|
| 11. |
examenvraagstuk
VWO Wiskunde B, 2017-I. |
| |
|
|
|
| |
De baan van een punt P wordt gegeven door de
volgende bewegingsvergelijkingen: |
| |
|
| |
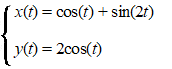 |
| |
|
|
|
| |
Met t in seconden en
x en y in meter.
Als t loopt van 0 tot 2π
, doorloopt P de baan
precies één keer.
In de figuur linksonder is deze baan weergegeven. Ook is te zien
waar P zich bevindt op t
=
0 en in welke richting P
zich dan beweegt. |
| |
|
|
|
| |
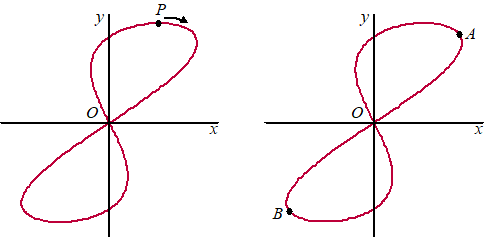 |
| |
|
|
|
| |
a. |
Bereken met behulp van differentiëren de maximale
snelheid van het punt P in meter per seconde. Rond je
antwoord af op één decimaal. |
| |
|
|
|
| |
Voor 0
≤
t ≤
2π
zijn er vier tijdstippen waarop
de x-coördinaat
en de y-coördinaat
van P
aan elkaar gelijk zijn. Op deze
tijdstippen bevindt
P zich achtereenvolgens in
de punten A,
O,
B
en
O.
Zie de figuur rechtsboven. |
| |
|
|
|
| |
b. |
Bereken exact hoeveel seconden de beweging van A
naar B duurt. |
| |
|
|
|
| |
Een punt Q maakt dezelfde beweging als P,
maar Q loopt π
seconden vóór op P.
De bewegingsvergelijkingen van Q zijn dan: |
| |
|
| |
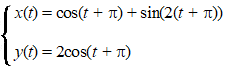 |
| |
|
|
|
| |
Als t
=
1/2π
en
als t = 3/2π
, vallen P en Q samen. Op alle andere tijdstippen
is er sprake van een lijnstuk PQ. |
| |
|
|
|
| |
c. |
Bewijs dat de helling van lijnstuk
PQ onafhankelijk van t is. |
| |
|
|
|
| 12. |
examenvraagstuk
VWO Wiskunde B, 2021-III.
Voor t ≥
0 beweegt het punt P1 volgens de
bewegingsvergelijkingen
x(t) = t2 + 2t
y(t) = 4t
Tegelijkertijd
beweegt het punt P2 volgens de
bewegingsvergelijkingen:
x(t) = 4t
y(t) = 2t2
Er is één tijdstip t waarop de punten P1 en
P2 gelijke snelheid hebben |
| |
|
|
|
| |
a. |
Bereken dat tijdstip. |
| |
|
|
|
| |
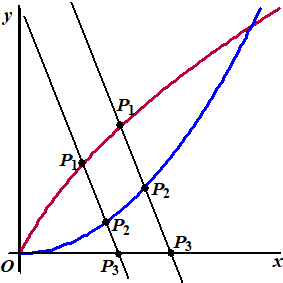
In onderstaande
figuur zijn beide banen getekend. Op twee tijdstippen,
namelijk t = 0 en t = 2, vallen P1
en P2 samen. Op alle andere tijdstippen kun je de
lijn l door P1 en P2
tekenen. In de figuur is dit voor twee tijdstippen gedaan. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
De
richtingscoëfficiënt van l is gelijk aan -2 voor elke waarde
van t (met t ≠ 0 en t ≠ 2 ). |
| |
|
|
|
| |
b. |
Bewijs dit. |
|
| |
|
|
|
| |
Voor elke
waarde van t (met t ≠ 0 en t ≠ 2 ) is P3
het snijpunt van l met de x-as. Zie de figuur, waarin
P3 is aangegeven voor twee verschillende
tijdstippen. |
| |
|
|
|
| |
c. |
Bereken exact
op welk tijdstip de x-coördinaat van P3
gelijk is aan 3. |
| |
|
|
|
| |
|
|
 |
| ©
h.hofstede (h.hofstede@hogeland.nl) |