| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Gemengde opgaven HAVO Wiskunde A. |
| |
| |
| |
| 1. |
vuistregels normaal
effectgrootte
wortelformule GR
grafiek aflezen
Op consultatiebureaus houdt men nauwkeurig de lengte
van baby’s bij.
De gemiddelde lengte van een pasgeboren baby was in Nederland in 2015
gelijk aan 50 cm.
Natuurlijk zijn niet alle pasgeboren baby’s even lang: L is de
gemiddelde lengte.
De lengtes zijn normaal verdeeld en de standaarddeviatie blijkt 8 cm te
zijn. |
 |
| |
|
|
|
| |
a. |
Als je de lengtes van 1600 pasgeboren baby's bekijkt, hoeveel van die
baby's
zullen dan een lengte tussen de 42 en 66 cm hebben? |
| |
|
|
|
| |
De arts van een consultatiebureau heeft in 2019 de lengte van alle
pasgeboren baby's in haar praktijk bijgehouden en zij vond een
gemiddelde lengte van 52 cm. De arts wil statistisch onderzoeken of dat
gemiddelde afwijkt van 50 cm. Gelukkig heeft zij wiskunde A op de
middelbare school gehad.
Zij berekent daarom de effectgrootte.
Zij vindt een effectgrootte van 0,4. Precies op de grens tussen
"gering" en "middelmatig". |
| |
|
|
|
| |
b. |
Bereken m.b.v. je GR hoe groot de
standaardafwijking van haar metingen zal zijn geweest. Leg ook met een
redenering uit of de effectgrootte bij grotere standaardafwijkingen
groter of kleiner zal zijn. |
| |
|
|
|
| |
Ook tijdens de eerste paar jaar van het leven wordt de gemiddelde lengte
van de baby's bijgehouden. Er blijkt te gelden: L = 20 + 10 • √(t
+ 9).
Daarin is L de lengte van een baby in cm en t de leeftijd in
maanden met t = 0 op het tijdstip van de geboorte. |
| |
|
|
|
| |
c. |
Onderzoek met deze formule in hoeveel tijd de lengte van een baby vanaf
de
geboorte verdubbelt. |
| |
|
|
|
| |
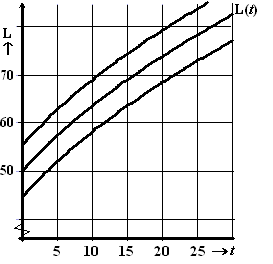
Om aan te geven wat een normale lengte is heeft de arts van het
consultatiebureau in de figuur hiernaast de grafiek van L getekend plus
de twee lijnen waartussen 50% van de baby’s zich bevindt. De baby's
tussen die beide lijnen noemen we "normaal".
Een trotse moeder beweert dat haar pasgeboren baby "normaal" was, en
na 20 maanden nog steeds " normaal" was, ondanks een groei van maar
liefst 80% |
 |
| |
|
|
| |
d. |
Onderzoek met de figuur of dat een sterk verhaal is, of dat dit
inderdaad in principe mogelijk is. |
| |
|
|
|
| |
| |
|
|
|
| 2. |
redeneren formule
breuk optellen
formule GR
Max Vcp
In een kroeg merkt men meestal dat er meer drankjes worden gekocht als
de temperatuur omhoog gaat.
Het percentage bezoekers (P) dat meer dan 6 drankjes koopt hangt af
van de temperatuur (T) volgens de formule: |
| |
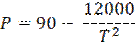 |
| |
|
|
|
| |
a. |
Laat met een duidelijke redenering zien dat bij stijgende temperatuur
het percentage inderdaad toeneemt, en bereken de grenswaarde van dit
percentage. |
| |
|
|
|
| |
b. |
Schrijf de formule voor P als één breuk. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
De drie gezusters en de Groote Griet zijn twee kroegen naast elkaar aan
de Grote Markt in Groningen.
De eigenaren vergelijken het aantal drankjes dat hun bezoekers op een
donderdagavond gebruikten.
Dat leverde de volgende tabel op. |
| |
|
|
|
| |
| Aantal drankjes |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Aantal klanten
Groote Griet |
5 |
12 |
34 |
45 |
20 |
14 |
7 |
5 |
4 |
1 |
Aantal klanten
Drie Gezusters |
4 |
6 |
26 |
31 |
35 |
25 |
10 |
8 |
8 |
4 |
|
| |
|
|
|
| |
c. |
Wat zal, gezien het aantal mensen dat bij de Groote Griet meer dan 6
drankjes nam, de temperatuur volgens bovenstaande formule zijn geweest?
|
| |
|
|
|
| |
d. |
Leg uit door het Max Vcp te berekenen of het verschil in
aantallen drankjes tussen beide kroegen gering, middelmatig
of groot is. |
| |
|
|
|
| |
| |
|
|
|
| 3. |
tellen
gemiddelde
betrouwbaarheidsinterval
parameter berekenen
grenswaarde beredeneren |
| |
|
 |
| |
Veel onderzoek in laboratoria wordt
gedaan aan muizen.
Om te testen of muizen slimmer zijn dan andere muizen laat men ze een
doolhof doorlopen waarbij aan het uiteinde een stuk kaas ligt.
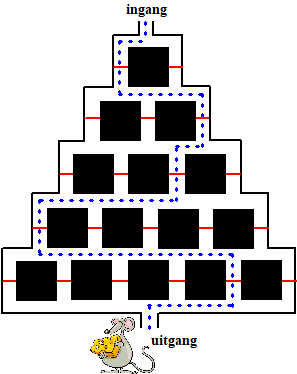
Hiernaast zie je zo'n doolhof. In elk van de verticaal getekende gangen
zit een rood klapdeurtje, dat slechts in één richting kan worden
gepasseerd. Dat verhindert dat een muis terug naar "boven" kan lopen.
Een muis kan langs een groot aantal routes van ingang naar uitgang
lopen. In de figuur is een voorbeeld van een route getekend. Twee routes
van ingang naar uitgang worden als gelijk beschouwd als dezelfde serie
klapdeurtjes wordt gepasseerd. |
| |
|
|
| |
a. |
Hoeveel verschillende routes zijn er van ingang naar uitgang in het
getekende doolhof? |
| |
|
|
|
| |
Daarbij meet men de gemiddelde tijd in seconden die het een muis kost om
de kaas te bereiken.
Van een grote controlegroep van 130 muizen is die doorlooptijd gemeten.
Daarbij heeft men verschil gemaakt tussen grijze muizen en witte
muizen. De groep bestond uit 80 witte muizen en 50 grijze. De gemiddelde
doorlooptijd van de hele groep bleek gelijk te zijn aan 228 seconden.
De gemiddelde doorlooptijd van de grijze muizen was 234 seconden.
|
| |
|
|
|
| |
b. |
Wat was de gemiddelde doorlooptijd van de witte muizen? |
| |
|
|
|
| |
Men onderzoekt of de muizen slimmer worden als men het
fosfodiësterase-4B (PDE4B) enzym blokkeert.
Dan kan door de muizen het middel Sidenafil toe te dienen.
Men noemt een muis "slimmer" als de doorlooptijd minder dan 228 seconden
is.
In het onderzoek bleek dat van de 130 muizen die Sidenafil toegediend
kregen, er 106 slimmer waren. |
| |
|
|
|
| |
c. |
Geef een 95%-betrouwbaarheidsinterval voor de proportie slimmere muizen
in deze groep. |
| |
|
|
|
| |
Hoe meer Sidenafil de muizen kregen toegediend, des te lager werd de
gemiddelde doorlooptijd. In de volgende tabel staan de gegevens van 5
muizen. |
| |
|
|
|
| |
| hoeveelheid Sidenafil (mg) |
0,83 |
1,54 |
1,92 |
2,24 |
2,41 |
| gemiddelde doorlooptijd (sec) |
224 |
200 |
186 |
175 |
169 |
|
| |
|
|
|
| |
d. |
Toon aan dat deze tabel bij benadering een lineair verband beschrijft en
geef een formule voor dat verband. |
| |
|
|
|
| |
Natuurlijk kan
dit effect niet alsmaar doorgaan want dan zouden de muizen op een
gegeven moment in nul seconden het doolhof doorlopen! Het blijkt
dat bij een dosis van 3 mg de doorlooptijd (D in sec) gelijk was
aan 148 sec, maar bij hogere doses neemt die doorlooptijd minder snel
af.
Vanaf D = 3 bleek te gelden: D = a/x
+ 253 |
| |
|
|
|
| |
e. |
Bereken de waarde van a |
| |
|
|
|
| |
f. |
Beredeneer met de formule dat de doorlooptijd nadert naar een bepaalde
grenswaarde. |
| |
|
|
|
| |
| 4. |
procentberekening
betrouwbaarheidsinterval
normale verdeling
spreidingsdiagram |
| |
|
| |
 |
| |
|
|
|
| |
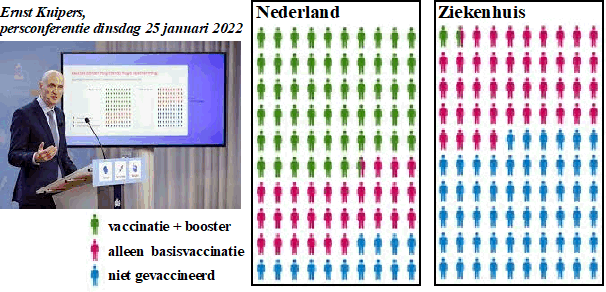
Hierboven zie je minister Kuipers van volksgezondheid op de
corona-persconferentie van dinsdag 25 januari 2022. Hij laat hier twee
diagrammen zien die rechts vergroot staan weergegeven.
Het linkerdiagram geeft aan hoeveel van de mensen in Nederland een
boostervaccinatie hebben of alleen een basisvaccinatie of niet
gevaccineerd zijn. Het rechterdiagram geeft deze aantallen voor de
mensen die vanwege corona in het ziekenhuis liggen.
Neem aan dat Nederland 17440000 inwoners heeft en dat er op 25 januari
1028 mensen vanwege corona in een ziekenhuis lagen. |
| |
|
|
|
| |
a. |
Bereken met deze gegevens hoeveel procent van de mensen met een
boostervaccinatie in het ziekenhuis liggen en hoeveel procent van de
ongevaccineerden in het ziekenhuis liggen.
Hoeveel keer zo groot is de kans om in het ziekenhuis te komen voor een
ongevaccineerde vergeleken met iemand met een boosterprik? |
| |
|
|
|
| |
Wilma Appie gelooft de cijfers van Kuipers niet. Zij leest af dat
ongeveer 56% van de mensen in het ziekenhuis ongevaccineerden zijn, en
denkt dat dat een veel te hoog aantal is.
Wilma belt met het UMCG in Groningen en krijgt van hen te horen dat er
bij hen 22 coronagevallen liggen waarvan 11 ongevaccineerd.
"Zie je wel: 50%! Die 56% is gewoon keihard gelogen" roept Wilma
woedend en ze gaat uiteraard direct een demonstratie organiseren. |
| |
|
|
|
| |
b. |
Bereken welk 95%-betrouwbaarheidsinterval Wilma op grond van de gegevens
uit Groningen mag opstellen voor de proportie ongevaccineerden in het
ziekenhuis in Nederland |
| |
|
|
|
| |
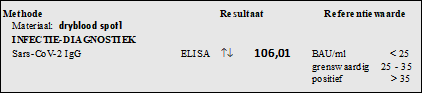
Na een vaccinatie heb je antistoffen in je bloed. De zogenaamde "spike-antistoffen
Sars-Cov-2".
De Euroimmun-test meet door een vingerprik de hoeveelheid van
deze antistoffen in je bloed. Hieronder zie je de uitslag van zo'n
test. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Deze uitslag was een waarde van 106,01.
Je ziet rechts dat waarden boven de 35 positief zijn, en tussen de 25 -
35 grensgevallen |
| |
|
|
|
| |
c. |
Als
na de eerste prik het aantal antistoffen normaal verdeeld is met een
gemiddelde van 45 en een standaardafwijking van 10, hoeveel procent
van die mensen zal dan na 3 dagen een positief resultaat hebben? |
| |
|
|
|
| |
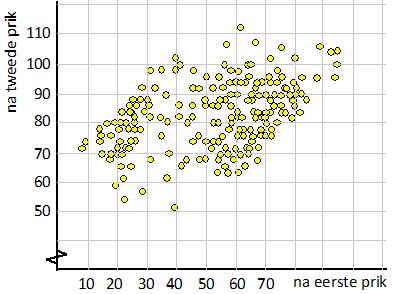
Een groot aantal mensen die met Astra-Zeneca zijn gevaccineerd heeft op
verzoek van de GGD 3 dagen na hun eerste prik en ook 3 dagen na hun
tweede prik de hoeveelheid antistoffen in hun bloed gemeten. Dat leverde
het volgende spreidingsdiagram op: |
| |
|
|
|
| |
 |
| |
|
|
|
| |
d. |
Leg
uit hoe je aan dit diagram kunt zien dat de hoeveelheden antistoffen 3
dagen na de eerste prik niet normaal verdeeld zijn |
| |
|
|
|
| |
e. |
Geef in de figuur op het werkblad aan bij welke mensen het aantal
antistoffen 3 dagen na de tweede prik meer dan dubbel zo groot was als 3
dagen na de eerste prik. |
| |
|
|
|
| |
| 5. |
standaardafwijking
klassenindeling
betrouwbaarheidsinterval
MaxVcp |
| |
Stappenteller
Twee groepen van 1000 HBO-studenten en 1000 Universiteits-studenten is
gevraagd om een poos een stappenteller te dragen en bij te houden
hoeveel stappen er gemiddeld per dag werden gezet.
Dat leverde de volgende tabel op: |
| |
|
|
|
| |
|
gemiddeld aantal
stappen per dag |
HBO |
Universiteit
|
|
2000 -< 4000 |
42 |
71 |
|
4000 -< 6000 |
96 |
243 |
|
6000 -< 8000 |
144 |
346 |
|
8000 -< 10000 |
251 |
102 |
|
10000 -< 12000 |
332 |
81 |
|
12000 -< 14000 |
103 |
60 |
|
14000 -< 16000 |
22 |
47 |
|
16000 -< 18000 |
10 |
50 |
|
| |
|
|
|
| |
Het gemiddelde van de HBO-studenten is ongeveer gelijk aan 9400 stappen
en de standaardafwijking is 2800 stappen.
Je zou deze twee getallen nauwkeuriger kunnen berekenen. |
| |
|
|
|
| |
a. |
Bereken deze twee getallen nauwkeuriger |
| |
|
|
|
| |
b. |
Leg duidelijk uit waarom zo'n nauwkeuriger berekening niet zinvol is. |
| |
|
|
|
| |
c. |
Bereken het 95%-betrouwbaarheidsinterval van het gemiddelde aantal
stappen van de HBO-studenten. |
| |
|
|
|
| |
d. |
Bereken met het Max Vcp of het verschil in stappen tussen deze twee
groepen gering, middelmatig of groot is.
|
| |
|
|
|
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|