|
|
 |
|
Hoogtelijnen. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
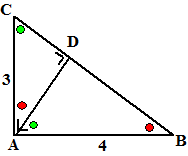
Als je een hoogtelijn in een rechthoekige
driehoek tekent krijg je de figuur hiernaast. Je kunt vast de schuine
zijde wel met Pythagoras berekenen; die is 5.
De andere lengtes in de figuur zijn te berekenen door gebruik te maken
van gelijkvormige driehoeken. Dit is één van de drie basisfiguren
die je in de vorige les hebt geleerd, dus dat moet lukken!
Daar vonden we dat ABC ~
DAC ~ DBA
Daarmee kun je dan een verhoudingsschema maken en allerlei lengtes gaan
uitrekenen. |
 |
Maar het kan handiger!
Hoe dat veel en veel sneller kan, kun je zien door de oppervlakte
van de driehoek uit te rekenen.
Die is gelijk aan 1/2
× basis × hoogte. In dit
geval 1/2
× 3 ×
4 = 6.
Misschien denk je nu "wat heb ik hier in vredesnaam aan", maar
het mooie komt als je deze driehoek andersom legt: |
| |
|
|
 |
| |
In de rechterfiguur kun je
natuurlijk ook de oppervlakte uitrekenen. Nu is de basis CB = 5 en
de hoogte AD, dus de oppervlakte is gelijk aan 1/2
× 5 ×
AD = 21/2AD
Maar die oppervlakte is tijdens het draaien niet veranderd natuurlijk!
Dus de oppervlakte van de rechterfiguur is nog steeds gelijk aan 6.
21/2AD
= 6 geeft heel eenvoudig AD = 2,4. |
| |
|
Waar
komt het op neer?
In de driehoek hierboven vonden we 1/2
× 3 ×
4 = 1/2
× 5
× AD.
Als je al die factoren 1/2
alvast weglaat staat er 3 × 4
= 5 × AD
Het algemene geval zie je in de driehoek hiernaast: c
× b = a
× h
Bedenk goed dat dit een erg snelle manier is, maar dat het alleen werkt
bij de hoogtelijn in een rechthoekige driehoek!!!! |
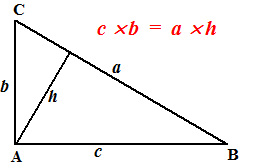 |
| |
|
|
OPGAVEN |
| |
|
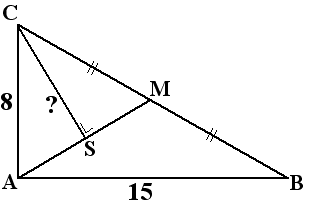
| 1. |
ABC is een
rechthoekige driehoek met AB = 15 en
AC = 8 en rechte hoek A.
AM is de zwaartelijn vanuit A
Teken een lijn door CS die loodrecht op deze zwaartelijn staat.
Hoe lang is CS? |
 |
| |
|
|
|
| |
|
|
|
| 2. |
Hoeveel procent van de oppervlakte van een rechthoekige driehoek
met zijden 3, 4 en 5 ligt
tussen de hoogtelijn en de zwaartelijn vanuit de rechte hoek? |
| |
|
|
|
| |
|
|
|
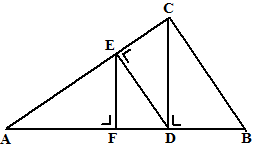
| 3. |
Hiernaast staat een rechthoekige
driehoek met zijden
AC = 8, BC = 6 en AB = 10.
Bereken de lengte van EF |
 |
| |
|
|
|
| |
|
|
|
|
4. |
Een rechthoekige driehoek heeft een
zijde van 30 en een hoogtelijn van 24.
Bereken de oppervlakte van deze driehoek. |
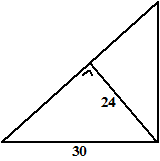 |
| |
|
|
|
| |
|
|
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|
|
| |
|