| |
 |
| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| Gemengde opgaven
gegevensverwerking |
| |
|
|
|
| 1. |
Examenopgave VWO,
Wiskunde A, 2008 |
| |
|
|
|
| |
Niet alleen
in fitnesscentra maar ook bij andere trainingen letten veel sporters
op hun hartslag. Ze gebruiken daarvoor een hartslagmeter.
De hartslag is het aantal keren dat het hart per
minuut klopt en wordt altijd op een geheel getal afgerond.
Bij een fitnesscentrum heeft men van alle nieuwe leden de hartslag gemeten
bij het begin van de eerste training. Het resultaat
daarvan is weergegeven in twee relatieve
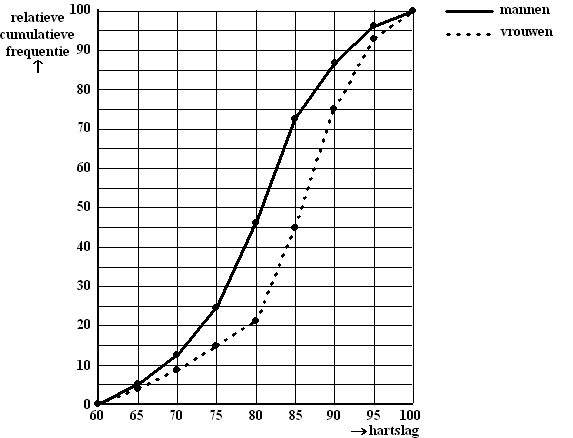
cumulatieve frequentiepolygonen. Zie de volgende figuur. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
In deze
figuur lees je bijvoorbeeld af dat 75% van de vrouwen een hartslag heeft
van 90 of lager.
Uit deze figuur kunnen we een boxplot afleiden
die hoort bij de verdeling van de hartslag van de vrouwen. |
| |
|
|
|
| |
a. |
Teken
deze boxplot. Licht je werkwijze toe. |
|
| |
|
|
|
| |
b. |
Hoe groot
zijn het gemiddelde en de standaardafwijking van de hartslag van de
vrouwen? Licht je werkwijze toe. |
| |
|
|
|
| 2. |
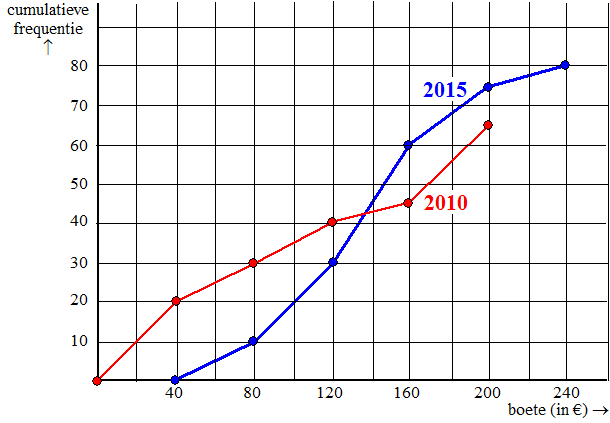
Hieronder
zie je één figuur twee cumulatieve frequentiepolygonen waarin de
verkeersboetes staan, die in een klein dorpje in een jaar zijn gegeven.
Op de x-as staat de hoogte van de boete in euro's. Er is een
grafiek voor het jaar 2010 en een grafiek voor 2015. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
a. |
Hoeveel procent is het totaal aantal boetes van 2010 naar 2015
toegenomen? |
| |
|
|
|
| |
b. |
Hoeveel procent van de boetes in 2015 was hoger dan €160 ? |
| |
|
|
|
| |
c. |
Bereken de gemiddelde hoogte van een boete in 2010. |
| |
|
|
|
| |
d. |
Teken onder de grafieken een boxplot voor de boetes in 2015. |
| |
|
|
|
| 3. |
In een enquête is een aantal mensen gevraagd hoeveel dagen per week zij
alcohol drinken. Dat gaf de tabel hieronder: |
| |
|
|
|
| |
| aantal dagen |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| aantal mensen |
23 |
40 |
62 |
68 |
18 |
12 |
4 |
2 |
|
| |
|
|
|
| |
a. |
Bereken zonder rekenmachine de mediaan van deze gegevens. Leg
duidelijk uit! |
| |
|
|
|
| |
b. |
Bereken de standaarddeviatie van deze gegevens. |
| |
|
|
|
| |
c. |
Als je een cirkeldiagram zou willen tekenen van deze gegevens, hoeveel
graden zou de hoek dan worden die bij de categorie "3 dagen" hoort?
Rond af op gehele graden |
| |
|
|
|
| |
d. |
De onderzoeksgroep bestond uit mannen en vrouwen en gaf een gemiddelde
van 2,35 dagen. Als je alleen de 180 mannen uit de groep zou bekijken
zou je een gemiddelde van 2,60 dagen vinden.
Hoeveel dagen dronken de vrouwen uit de groep gemiddeld alcohol? |
| |
|
|
|
| 4. |
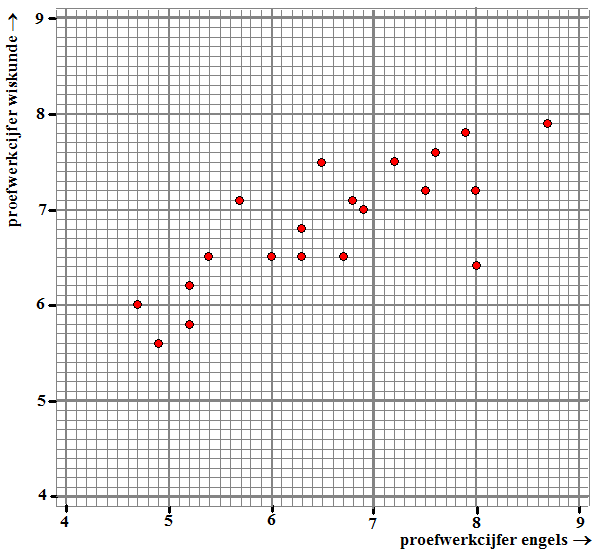
Hieronder
zie je een spreidingsdiagram waarin voor 20 leerlingen het
proefwerkcijfer engels (x-as) en het proefwerkcijfer wiskunde (y-as)
staan uitgezet. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
a. |
Leg zonder berekening te maken uit welk van beide cijfers
de grootste standaarddeviatie zal hebben. |
| |
|
|
|
| |
b. |
Hoeveel leerlingen hadden op Engels een hoger cijfer dan op wiskunde? |
| |
|
|
|
| |
c. |
Geef de modus en de mediaan van de wiskundecijfers. |
| |
|
|
|
| |
d. |
Maak van
deze figuur een dubbel steel- en blad-diagram. |
| |
|
|
|
| 5. |
Examenopgave HAVO
wiskunde A, 2017-I |
| |
|
|
|
| |
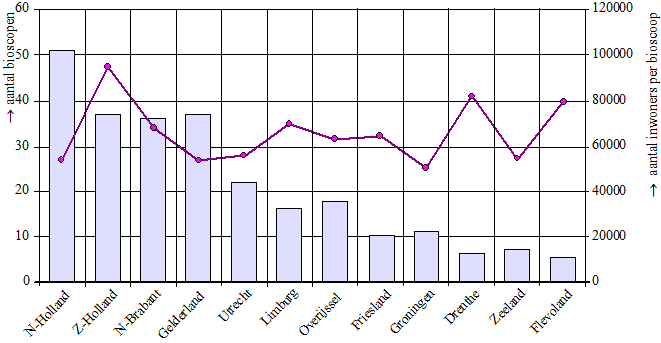
In de figuur staan gegevens over
bioscopen in Nederland in 2012. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Het staafdiagram geeft het aantal bioscopen per
provincie weer (linker verticale as). Het lijndiagram toont het
aantal inwoners per bioscoop uitgesplitst per provincie (rechter
verticale as).
In de tabel staat per provincie het aantal bioscoopbezoeken in
2012. |
| |
|
|
|
| |
| provincie |
bezoeken |
| N-Holland |
7532000 |
| Z-Holland |
7298000 |
| N-Brabant |
4366000 |
| Gelderland |
2695000 |
|
|
| provincie |
bezoeken |
| Utrecht |
2009000 |
| Overijssel |
1663000 |
| Limburg |
1662000 |
| Groningen |
1180000 |
|
|
| provincie |
bezoeken |
| Friesland |
625000 |
| Flevoland |
525000 |
| Drenthe |
519000 |
| Zeeland |
486000 |
|
|
| |
|
|
|
| |
Kees beweert: “In de provincie met de meeste
bioscopen per inwoner is het gemiddeld aantal bioscoopbezoeken per
inwoner meer dan 2.”
Onderzoek over welke provincie Kees het heeft en
bereken voor deze provincie of hij gelijk heeft. |
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|