| |
 |
|
f (x) = p. |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
Omdat f(x)
natuurlijk gewoon het zelfde is als y (namelijk wat er
uitkomt als je x in de gegeven formule invult) betekent
f(x) = p eigenlijk dus gewoon
y = p, waarbij p één of
ander constant getal is. |
 |
| |
Met de grafiek.
Maar als je dat in "grafiektaal" wilt vertalen, dan stelt y
gewoon de hoogte van de grafiek voor, dus staat er eigenlijk dat
de hoogte van de grafiek gelijk moet zijn aan p. |
| |
|
|
|
|
f
(x) = p ⇔
bij welke x is de hoogte van de grafiek gelijk aan
p ??? |
|
| |
|
|
|
Het antwoord op zo'n vraag is dan
ook gemakkelijk te vinden: teken gewoon een horizontale lijn op hoogte
p en kijk waar (bij welke x-waarden) die de grafiek
snijdt.
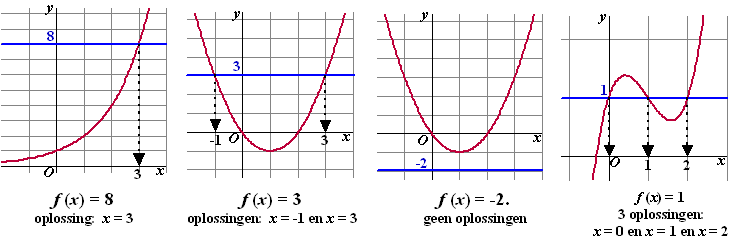
Hieronder zie je een aantal grafische oplossingen: |
| |
|
|
|
|
 |
| |
|
|
|
Je ziet hierboven direct al dat
het aantal oplossingen van de vergelijking f(x) = p
nogal afhangt van p. In deze voorbeelden varieerde het aantal
oplossingen van 0 tot 3, maar het zouden er bij andere grafieken
natuurlijk gemakkelijk nog veel meer dan 3 kunnen zijn.
Kijk eens naar die grafiek helemaal hier rechtsboven...... Het is de
grafiek van y = x3 - 3x2 + 2x
+ 1.
Stel dat de vraag zou zijn: "Voor welke p heeft de
vergelijking f(x) = p precies twee oplossingen?" |
| |
|
|
|
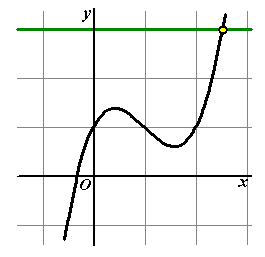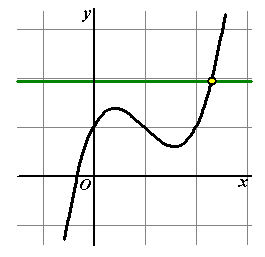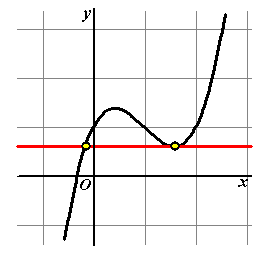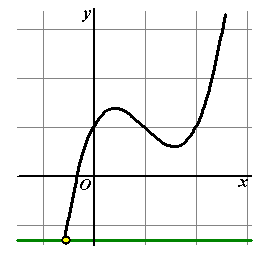
Hiernaast zie je wat
er in het rechterplaatje voor verschillende waarden van p gebeurt.
De groene lijnen geven 1 snijpunt (dus 1 oplossing), de rode lijnen
geven 2 snijpunten (2 oplossingen) en de blauwe lijnen geven 3
snijpunten (3 oplossingen).
De vraag: "Voor welke p heeft de
vergelijking f(x) = p precies twee oplossingen?"
is dus precies dezelfde vraag als: "Waar zitten de rode lijnen?"
En aan de figuur zie je dan weer dat dat ook dezelfde vraag is als:
"Waar zitten de maxima en minima van de grafiek?"
|
 |
| |
|
|
|
|
 |
| |
|
|
|
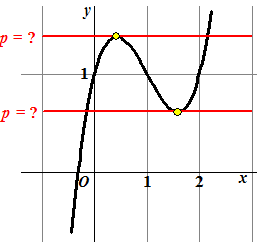 |
Nou, die laatste
vraag heb je al veel vaker beantwoord natuurlijk. Los het op met je
rekenmachine (calc - maximum/minimum) of als je dat kunt algebraïsch met de afgeleide
(f ' = 0). Denk er daarbij wel om dat de waarde van p
gelijk is aan de y-waarde van het gevonden maximum/minimum.
In
het bovenstaande geval geeft dat trouwens de oplossingen p
≈ 1,38
en p
≈ 0,62. Dat zijn dus die rode p's
in de figuur hiernaast.
|
|
| |
|
| |
|
|
OPGAVEN |
| |
|
| 1. |
Gegeven is de functie
f(x) = x3 - 6x + 8
Voor welke p heeft de vergelijking f(x)
= p drie oplossingen?
Geef je antwoord in twee decimalen nauwkeurig. |
| |
|
| |
|
| 2. |
Gegeven is de functie
f(x) = 2x + 6 + 1/x
Voor welke p heeft de vergelijking f(x)
= p twee oplossingen?
Geef je antwoord in twee decimalen nauwkeurig. |
| |
|
| |
|
|
|
|
| 3. |
Gegeven is de functie
f(x) = (x²
- 8)/(4x + 4)
De lijn y = p snijdt de grafiek van f
in de punten A en B.
Bereken p als AB = 8 |
| |
|
|
|
|
| |
|
|
|
|
| 4. |
examenvraagstuk HAVO
wiskunde B, 2016-II |
| |
|
|
|
|
| |
De functie f is gegeven door:
|
| |
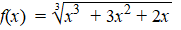 |
| |
De grafiek van f
snijdt de x-as in drie punten. Zie de figuur. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
a. |
Bereken de x-coördinaten van de drie snijpunten
van de grafiek van f met de x-as. |
| |
|
|
|
|
| |
Verder is gegeven de horizontale lijn l met
vergelijking y = p . De grafiek van f snijdt l
in drie punten. |
| |
|
|
|
|
| |
b. |
Bereken voor welke waarden van p dit het geval
is. Rond de getallen in je antwoord af op drie decimalen. |
| |
|
|
|
|
| |
|
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|
|
|
| |
|
|
|