© h.hofstede (h.hofstede@hogeland.nl)

De exponentiële formule: het algemene geval.
De algemene vorm van een exponentiële formule was:

y = B • gx
We gaan nu uit een willekeurige exponentiële tabel of grafiek of verhaaltje zo'n exponentiële formule opstellen.
De beginwaarde B.
In de les over groeifactoren staat hoe je een groeifactor kunt vinden.
Als we de groeifactor hebben, dan is verder voor een volledige formule alleen nog de beginwaarde B nodig. Hoe kun je die vinden? Simpel:
Vul gewoon een punt in!

Voorbeeld:
Een exponentieel proces y = B • gx  heeft groeifactor 1,2 en bij x = 4 hoort  y = 34. Geef de formule.

Oplossing:
De algemene formule zal zijn  y = B • 1,2x
Vul het punt (2, 34) in:  34 = B • 1,24  = B • 2,0736  ⇒  B = 34/2,0736 = 16,4
Kortom: y = 16,4 • 1,2x 

   
Vier Soorten Berekeningen met de Exponentiële Formule.

OK, de exponentiële formule  y = B • gx  heeft 4 letters, namelijk een y, een B, een g en een x,
Daarom kunnen er in principe ook 4 soorten vragen gesteld worden, waarbij steeds één van de vier letters onbekend is. Die onbekende moet je dan berekenen, en de andere drie kun je op de één of andere manier uit het verhaaltje bij de vraag halen.

Van alle vier dan maar een voorbeeldje?  Vooral om even samen te vatten welke rekentechnieken je wanneer moet gebruiken.
   
 
Berekening 1.  y is onbekend.
Het aantal kakkerlakken in een flatgebouw neemt elke week met 8% toe.
Nu zijn het er 850.  Hoeveel zijn het er over 10 weken?

oplossing:   B = 850, g = 1,08  en  x = 10.  Gewoon invullen:   y = 850 • 1,0810 = 1835.

y = B ·gx
   
 
Berekening  2.  B is onbekend.
Een bank geeft mij 2,3% rente per jaar.
Hoeveel moet ik nu op een rekening zetten om over 15 jaar  €10000 te hebben?

oplossing:  y = 10000, g = 1.023,  x = 15. 
Invullen geeft:  10000 = B • 1,02315
10000 = B • 1,406 ⇒   B = 10000/1,406 = €7110

y = B ·gx
   
 
Berekening  3.  g is onbekend.
Het aantal inwoners van een stad is de laatste 12 jaar afgenomen van 56000 naar 32500.
Hoeveel procent afname per jaar is dat? 

oplossing:  y = 32500,  B = 56000,  x = 12. 
Invullen geeft  32500 = 56000 • g12
g12 = 32500/56000 = 0,5803  ⇒   g = 0,58031/12 = 0,9557
Dat is een afname van 4,43% per jaar.

y = B ·gx
   
 
Berekening  4.  x is onbekend.
Het aantal bacteriën in een biefstuk verdubbelt elke dag.
Als het er nu 200 zijn, hoe lang duurt het dan voordat het er 1 miljard zijn?

oplossing:  y = 1000000000,  B = 200, g = 2
Invullen geeft  1000000000 = 200 • 2x
2x = 1000000000/200 = 5000000
⇒ x = log5000000/log2 = 22,2 dagen

y = B·gx
   
 
Berekening  4.  x is onbekend.
Het aantal bacteriën in een biefstuk verdubbelt elke dag.
Als het er nu 200 zijn, hoe lang duurt het dan voordat het er 1 miljard zijn?

oplossing:  y = 1000000000,  B = 200, g = 2
Invullen geeft  1000000000 = 200 • 2x
Die kunnen we voorlopig niet algebraïsch oplossen.
Duur maar de GRL
Y1 = 1000000000
Y2 = 200 ×× 2x
intersect geeft

y = B·gx
1. Geef een formule voor onderstaande exponentiële tabellen.
x 18 22 26 30 34
y 362 655 1185 2146 3886
x 11 16 21 26 31
y 683 528 409 316 245
x 120 130 140 150 160
y 2994 2707 2449 2215 2003
x 6 14 22 30 38
y 0,309 0,322 0,335 0,348 0,363
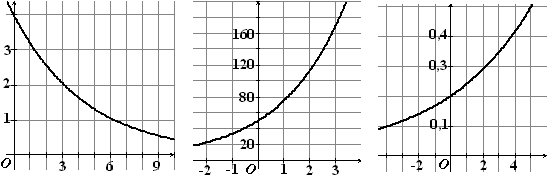
2. Geef een formule die hoort bij onderstaande exponentiële grafieken.

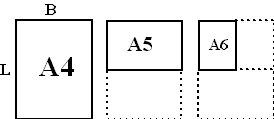
3. Wiskunde is overal!
Zelfs als je een brief voor Frans of zo zit te schrijven heb je eigenlijk wiskunde voor je neus. Letterlijk. Het velletje papier waar je op schrijft heeft namelijk meestal het zogenaamde A4-formaat.
Hoe zit dat precies in elkaar?
Als je een A4-formaat dubbel vouwt langs de langste zijde krijg je een A5-formaat.
A5 vouwen geeft A6, enzovoorts.

Het leuke is: al deze formaten zijn gelijkvormig! Dat wil zeggen dat de verhouding tussen lengte en breedte het zelfde is. 
   
a. Laat zien dat daaruit volgt  L = B • √2
   
b. De serie papierformaten begint bij A0 en A0 heeft een oppervlakte van precies 1 m2. Laat zien dat dan voor de lengte (in meter) van formaat An geldt:  L(n) = 1,19 • (0,71)n
4. Een aantal leerlingen van het HHC is het niet eens met het drankbeleid op leerlingavonden. Ze besluiten stiekem een reuzenfles jenever mee te nemen en verstoppen die samen met een borrelglas in de stortbak van de jongens-W.C. Ze spreken af om de fles tegen het eind van de avond aan te breken.

Echter, een groot aantal van hen krijgt al eerder wel trek. Ze spelen vals, en nemen als ze zogenaamd naar de WC gaan stiekem een lekkere borrel. Steeds precies een borrelglas vol. Omdat de rest straks niet mag merken dat er al uit de fles is gedronken vullen ze hem netjes weer bij met kraanwater.

De fles bevatte oorspronkelijk 2 liter jenever (35% alcohol). In het borrelglas gaat 15 cl.  Neem aan dat het kraanwater zich direct geheel vermengt met de jenever.

Voor het alcoholpercentage (P) van de drank in de fles als de nde  persoon wil gaan drinken geldt bij  benadering :      P(n) = 37,8 . (0,925)n  
a. Toon dat aan.
   
b. De hoeveelste drinker krijgt drank van nog maar 10% alcohol?

 de 18e
   
5. De luchtdruk neemt af met de hoogte.  De volgende tabel geeft daar informatie over:
   
 
hoogte in m 0 1000 2000 3000 4000 5000 6000 7000 8000
luchtdruk in mb 1013 897 793 702 621 550 487 431 381
   
  Laat zien dat de luchtdruk (P, in mb) een exponentiële functie is van de hoogte h (in duizenden meters) en geef een functievoorschrift voor deze functie.
   
Als de x-waarden helemáál niet regelmatig zijn.
Neem de volgende tabel:
x 2 5 13 19 30 50
y 4,6 5,8 10,9 17,3 40,3 187,6
1.  Als gegeven is dat het een exponentieel proces betreft.
Da's een makkie: je kiest gewoon twee punten uit de tabel. 
bijvoorbeeld de eerste en de laatste: (2, 4.6) en (50, 187.6)
daartussen geldt  een groeifactor  187,6/4,6 = 40,78 maar dat is in 50 - 2 = 48 stappen dus dat is g48 
g48 = 40,78  geeft  g = 40,781/48 = 1,08
gebruik  bijv. (2, 4.6) om nu B te berekenen:  4,6 = B • 1,082  ⇒  B = 3,9
De formule is  dus  y = 3,9 • 1,08x
2. Als je moet aantonen dat het exponentieel is.
bekijk de groeifactoren per "etappe":

tussen x = 2 en x = 5:  3 stappen dus  g3 = 5,8/4,6 = 1,2826  ⇒  g = 1,28261/3 = 1,080
tussen x = 5 en x = 13:  8 stappen dus  g8 = 10,9/5,9 = 1,847  ⇒  g = 1,8471/8 = 1,080
tussen x = 13 en x = 19:  6 stappen dus  g6 = 17,3/10,9 = 1,587  ⇒  g = 1,5871/6 = 1,080
tussen x = 19 en x = 30:  11 stappen dus  g11 = 40,3/17,3 = 2,329 ⇒  g = 2,3291/11 = 1,080
tussen x = 30 en x = 50:  20 stappen dus  g20 = 187,6/40,3 = 4,655 ⇒  g = 4,6551/20 = 1,080  

Die zijn allemaal gelijk dus het is een exponentiële tabel, en dan kun je zoals hierboven bij onderdeel 1 de formule opstellen (de g is trouwens 1,08, dat heb je intussen al gevonden).
6. Geef een formule voor onderstaande exponentiële tabellen. Toon eerst aan dat het gaat om een exponentieel verband.
x 0,9 4,5 6,2 8,9 12,1 13,4
y 8,5 70 191 935 6134 13171
x -8,7 -7,6 -4,4 -3,5 -2,1 -1,8
y 5,00 4,45 3,18 2,89 2,50 2,42
7. Een hoeveelheid water in een reservoir wordt verwarmd.
Na 5 minuten verwarmen is de temperatuur  24ºC en na 13 minuten is de temperatuur 30ºC
Neem aan dat de temperatuur lineair van de tijd afhangt.
   
a. Geef in dat geval een formule voor de temperatuur als functie van de tijd.
 

T = 0.75t + 20,25

b. Bereken met deze formule hoe groot de begintemperatuur was.

20,25

Neem vervolgens aan dat de temperatuur exponentieel van de tijd afhangt.
   
c. Geef in dat geval een formule voor de temperatuur als functie van de tijd.
 

T = 20,87 · 1,028t 

d. Bereken met deze formule hoe groot de begintemperatuur was.

T = 20,87

   
8. Het stralingsniveau (S) op en bepaalde plaats direct na het inslaan van een langeafstandsraket met nucleaire kop hangt af van de afstand (a in km) tot de plaats van inslag. Metingen leverden de volgende tabel:
stralingsniveau (S) 161000 108000 32600 12000 4400
afstand (a) 2 4 10 15 20
Er blijkt te gelden  S(a) = 240000 • 0,8a
a. Leg duidelijk uit hoe deze formule uit bovenstaande tabel valt af te leiden. Toon daarbij eerst aan dat het hier gaat om exponentiële afname.
   
b. De voor een mens dodelijke dosis straling is 200 of meer. Tot welke afstand vanaf de plaats van inslag zullen er direct doden gaan vallen?

31,77 km

   
9. Examenvraagstuk VWO Wiskunde A, 2005

Vijverbezitters kunnen tegenwoordig bij een tuincentrum laten onderzoeken of het water in hun vijver van goede kwaliteit is. Met een eenvoudige test kan van het water zowel de hardheid,  aangegeven met KH (carbonaathardheid), als de zuurgraad,  aangegeven met pH, worden vastgesteld. Deze twee waarden bepalen op hun beurt het CO2-gehalte van het water. Het CO2-gehalte, dat we in deze opgave zullen aangeven met C, is een belangrijke indicator voor de kwaliteit van het vijverwater. Met behulp van de volgende tabel kan bij gegeven KH en pH de waarde van C worden bepaald.
   
 
 

pH
6,0 6,4 6,8 7,2 7,6 8,0
KH
12
10
8
6
5
4
3
2
480,0 191,1 76,1 30,3 12,1 4,8
400,0 159,2 63,4 25,2 10,0 4,0
320,0 127,4 50,7 20,2 8,0 3,2
200,0 79,6 31,7 12,6 5,0 2,0
160,0 63,7 25,4 10,1 4,0 1,6
120,0 47,7 19,0 7,6 3,0 1,2
80,0 31,8 12,7 5,0 2,0 0,8
   
  De waarde van KH wordt in gehele getallen weergegeven; de waarde van pH wordt altijd met een nauwkeurigheid van 0,1 weergegeven. Uit de tabel lezen we bijvoorbeeld af dat voor vijverwater met KH = 5 en pH = 7,2 geldt: C = 12,6.

Als je voor pH een vaste waarde kiest, dan hangt C alleen nog maar af van KH. In de kolommen  van de tabel is te zien dat bij iedere vaste waarde van pH er een lineair (en zelfs evenredig) verband is tussen KH en C.

In de tabel is de rij die hoort bij KH = 6 leeg gelaten.

   
  a. Bereken welk getal er moet komen te staan op de plaats die hoort bij KH = 6 en pH = 6,8.
       

38,0

  Als je voor KH een vaste waarde kiest, dan hangt C alleen nog maar af van pH. Bij iedere vaste waarde van KH bestaat er een exponentieel verband tussen pH en C: als pH met 1 toeneemt, neemt C met 90% af.

Bekijk de rij die hoort bij KH = 4
         
  b. Laat door middel van berekeningen zien dat alle waarden van C in deze rij in overeenstemming zijn met het bovengenoemde exponentiële verband tussen pH en C en met de genoemde afname van 90%.
         
  Volgens de folder is het water in de vijver van goede kwaliteit als voldaan is aan de volgende drie voorwaarden:
  I de KH-waarde van het water moet tenminste 6 en ten hoogste 10 zijn.
  II de pH-waarde van het water moet tenminste 7 en ten hoogste 8 zijn.
  III de C-waarde van het water moet tenminste 10 zijn.
         
  Een vijverbezitter laat zijn vijverwater testen. Bij de test worden de volgende waarden gemeten: pH = 7 en KH = 8. Op basis van bovenstaande tabel kan de bijbehorende waarde voor C worden berekend. Vervolgens kan worden nagegaan of voldaan is aan de drie voorwaarden voor goede waterkwaliteit.
         
  c. Bereken deze bijbehorende waarde van C en onderzoek daarmee of dit vijverwater van goede kwaliteit is.
       

C = 32

         
10. Examenvraagstuk VWO Wiskunde A, 2009

Koeien worden tegenwoordig gemolken door een zogenaamde melkrobot. De melkrobot melkt de koe zonder dat de boer daarbij aanwezig hoeft te zijn. In 2005 werd door de dierenbescherming het volgende persbericht gepubliceerd:
         
 

persbericht.

“In 2002 bleef 10% van de melkveestapel in de stal. De melkrobot heeft tot gevolg dat er steeds minder koeien in de wei komen. De dierenbescherming is daarom tegenstander van melkrobots. Dit jaar (2005 dus) blijft maar liefst 17% van de melkveestapel het hele jaar in de stal. Daardoor blijven de weilanden leeg. Als deze trend zich doorzet, verwachten wij dat over zo’n tien jaar de helft van de melkveestapel uit het Nederlandse landschap is verdwenen.”
         
  Uit het persbericht blijkt dat 90% van het melkvee in 2002 in de wei komt. Ook zien we dat in 2005 nog slechts 83% van het melkvee in de wei komt. In het persbericht is sprake van een ‘trend’, maar het wordt niet duidelijk van welk model men daarbij is uitgegaan en waar “de helft van de melkveestapel” vandaan komt. Enkele voor de hand liggende modellen zijn:
  1. een trend waarbij het percentage melkvee dat in de wei komt lineair daalt;
  2. een trend waarbij het percentage melkvee dat in de wei komt exponentieel afneemt.
         
  a. Bereken hoeveel procent van het melkvee in 2015 volgens model 1 en hoeveel procent volgens model 2 in de wei komt.
       

59,7 en 63,3

  Voor het beschrijven van de situatie op de lange duur is model 1 op grond van wiskundige overwegingen niet bruikbaar maar model 2 misschien wel.
         
  b. Leg uit waarom model 1 op de lange duur zeker niet realistisch kan zijn, maar model 2 misschien wel.
         
 

© h.hofstede (h.hofstede@hogeland.nl)