elasticiteit


Elasticiteit.	© h.hofstede (h.hofstede@hogeland.nl)

Als je van een artikel de prijs verandert, dan zal in het algemeen ook het aantal verkochte artikelen veranderen. Meestal zal de vraag naar een product afnemen als de prijs toeneemt. Economen vinden het erg interessant hoe snel de vraag naar een product verandert als de prijs verandert.

Laten we drie eenvoudige gevallen bekijken (q is steeds de vraag, p de prijs).

geval 1.
Stel dat geldt q = 800 - 4p
Dat betekent bijvoorbeeld dat bij een prijs van €12,50 een vraag van 750 hoort.
Als die prijs nu verandert van €12,50 naar €17,50 dan verandert de vraag van 750 naar 730.
Dus als de prijs €5,- toeneemt, dan neemt de vraag 20 af.

geval 2.
Stel dat geldt q = 24000 - 4p
Dat betekent dat bij een prijs van €10,50 een vraag van 23958 hoort, en bij een prijs van €15,50 een vraag van 23938.
Ook hier betekent een prijstoename van €5,- een vraagafname van 20.

geval 3.
Stel dat geldt q = 35000 - 4p
Dat betekent dat bij een prijs van €1200 een vraag van 30200 hoort en bij een prijs van €1205 een vraag van 30180.
Alweer betekent een prijstoename van €5,- een vraagafname van 20.

En toch vinden economen dat in deze drie gevallen de vraag heel verschillend reageert op de prijs!
Jij ook???

Hoe komt dat?

In het tweede geval is de vraagafname van 20 eigenlijk te verwaarlozen ten opzichte van de totale vraag van zo'n 25000. Of je nou 23958 artikelen verkoopt of 23938, daar zal geen handelaar van wakker liggen. Eigenlijk reageert de vraag hier dus amper op de prijs.
In het derde geval is er eigenblijk amper een prijsafname. Of je nou iets verkoopt voor €1200 of voor €1205, dat zal ook niet echt een winkelier de das om doen! Maar bij zo'n minieme prijsverandering is er toch al een vraagafname van 20. Dat betekent dat de vraag juist vrij heftig reageert op de prijs.
Samengevat:

Je moet alles relatief zien!

Economen gebruiken daarom als maat voor de vraagverandering bij een bepaalde prijsverandering een getal dat ze de elasticiteit noemen. Om precies te zijn:

in formule:

Als dit getal E_pq groot is, dan reageert de vraag sterk op prijsverschillen en als het klein is juist heel weinig.
De drie gevallen hierboven geven elasticiteiten -0,07 en -0,002 en -0,16 (reken zelf maar na).

Prijselasticiteit bij één bepaalde prijs.
Hiervoor ging het steeds over een prijstoename tussen twee prijswaarden.
Als men het heeft over de prijselasticiteit bij één bepaalde prijs dan wordt bedoeld de elasticiteit als p een heel klein beetje toeneemt. Dan verandert p met dp en daardoor q met dq en dat geeft in de formule voor E:

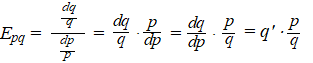
Die ^dq/_dp dat was een oude bekende: de afgeleide q'(p).

Voorbeeld.
Voor de vraag naar een bepaald product geldt: q = - p² - 20p + 1600.

a. Bereken E_pq als p toeneemt van €12 naar €18.

p = 12 geeft q = 1216 en p = 18 geeft q = 916 dus Δp = 6 en Δq = -300
^Δ^q/_q = ^-300/₉₄₄ = -0,318 en ^Δ^p/_p = ⁶/₁₂ = 0,5 dus E_pq = ^-0,318/_0,5 = -0,64.

b. Bereken E_pq bij een prijs van p = €12.

Bij p = 12 hoort q = 1216
q'(p) = -2p - 10 dus q'(12) = -2 • 12 - 10 = -34
E_pq = -34 • ¹²/₉₄₄ = -0,43.

OPGAVEN

Voor de vraagfunctie bij een bepaald artikel geldt q = -0,1p³ + 1,5p² - 7,5p + 100 voor 0 < p < 14

Bereken de prijselasticiteit van de vraag als p afneemt van €12,50 naar €12,00.

-4,35

Bereken de prijselasticiteit van de vraag bij een prijs p = €10,00

-1

Bij een bepaalde prijs (behalve p = 0) is de elasticiteit nul. Welke prijs is dat?
Hoe kun je die prijs in de grafiek van q(p) terugvinden?

p = 5

Voor een bepaald artikel geldt de vraagfunctie: q = 1200 - 3,5p
De grafiek van q staat hiernaast.

Bereken E_pq :
• als p stijgt van 100 naar 106
• als p stijgt van 100 naar 114
• als p daalt van 100 naar 88

Leg uit waarom vraag a) drie dezelfde antwoorden oplevert.

Als p van 0 naar 300 toeneemt zal E_pq dan toenemen of afnemen? Geef een uitleg zonder berekeningen te maken.

Een oliebollenbakker verkoopt per dag 800 zakken oliebollen voor een prijs van €6,- per zak.
Hij ontdekt dat elk dubbeltje prijsverlaging leidt tot 5 extra verkochte zakken, en elk dubbeltje prijsverhoging tot 5 zakken minder verkocht.
Dan volgt daaruit dat q = 1100 - 50p

Toon dat aan.

Bereken de prijselasticiteit van de vraag als de prijs toeneemt van €6,00 naar €7,00

-0,375

Bereken E_pq bij een vraag van 650 zakken oliebollen.

-0,69

Bereken bij welke prijs de opbrengst van de bakker maximaal zal zijn.

-11

Toon aan dat bij functies van de vorm q(p) = a • p^b (met a en b constanten) de elasticiteit bij elke prijs hetzelfde zal zijn.