© h.hofstede (h.hofstede@hogeland.nl)
Formules maken met de eenheidscirkel.
   
Hiernaast zie je nog eens de eenheidscirkel waarin je bij een hoek α de bijbehorende sinα en cosα kunt vinden; dat zijn het rode en het blauwe lijnstuk.

Dit plaatje geeft de mogelijkheid om zelf formules te maken!

Dat gaat met de volgende vijf stappen:
1.  teken zomaar een hoek α in de eenheidscirkel.
2.  waar ligt dan de hoek die gevraagd wordt?
3.  welk lijnstuk is de sinus/cosinus van die hoek?
4.  waar vind ik dat lijnstuk nog meer?
5.  is het inderdaad positief /negatief?

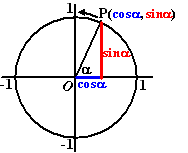
Stel bijvoorbeeld dat je sin(π - α) wilt veranderen in een andere formule.
Dan gaat dat zó:

   
   
In het vierde plaatje zie je dat beide lijnstukken gelijk zijn, (en ook beiden positief (stap 5)), dus geldt  sin(π - α) = sinα

AHA!! Een formule afgeleid:
   

sin(π - α) = sinα

   
En zo kun je heel veel formules zelf afleiden.

Let wel goed op het teken!

Denk erom dat sinus of cosinus niet precies gelijk zijn aan de lengte van die lijnstukjes. Het zijn eigenlijk de x- en de y-coördinaten van het punt op de eenheidscirkel. Die kunnen dus ook heel goed negatief zijn! Daar moet je met je formules wel rekening mee houden.
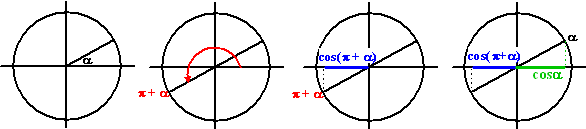
Neem de volgende formule voor  cos(π + α):
   

   
In het laatste plaatje zijn dat blauwe (cos (π+α)) en dat groene (cosα) lijnstukje wel even lang, maar de groene hoort bij een positieve x-coördinaat en de blauwe bij een negatieve. dus cos(π+α) en cosα verschillen van teken.
De formule wordt dus  cos(π+α) = -cosα. Let op dat minteken!!
Wáár dat minteken staat doet er natuurlijk niet toe, je kunt van dit voorbeeld ook maken  -cos(π+α) = cosα
   
Een nuttige formule.

In  het volgende voorbeeld wordt op deze manier een formule afgeleid die erg nuttig is.

Voorbeeld.   Waaraan is sin(1/2π - α)  gelijk?
Ik hoop dat de volgende vier plaatjes nu voor zich spreken:
   

   
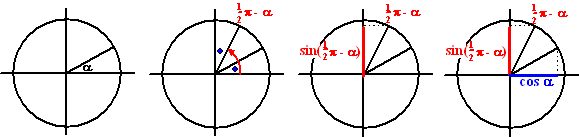In het laatste plaatje zie je dat  sin(1/2π - α) = cos(α)
En op precies dezelfde manier is af te leiden dat: cos(1/2π - α) = sin(α)
Deze twee komen erg vaak voor, want ze geven een manier om sinus in cosinus te veranderen (en andersom).
Misschien is het de moeite waard deze twee daarom uit je hoofd te leren.
   

sin(1/2π - α) = cos(α)
cos(1/2π - α) = sin(α)
   
Vergelijkingen oplossen.
 
Die nieuwe formules die je nu kunt afleiden kun je natuurlijk gebruiken om vergelijkingen op te lossen.

Twee voorbeelden.

Voorbeeld 1.  Los op in [0, 2π]:   sin2x + sin(1/4π - x) = 0
sin2x + sin(1/4π - x)  = 0   ⇒ sin2x = -sin(1/4π - x)
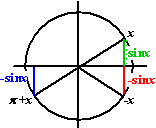
in de figuur hiernaast zie je aan het rode lijntje dat  -sinx  gelijk is aan  sin(-x)
(aan het blauwe kun je zien dat ook geldt  -sinx = sin(π + x), maar we kiezen de eenvoudigste formule)
dus  -sin(1/4π - x) = sin(-(1/4π - x)) = sin(-1/4π + x)

Daarmee wordt de vergelijking:  sin2x = sin(-1/4π + x)
⇒  2x =  -1/4π + x + k • 2π  ∨  2x = π - (-1/4π + x) + k • 2π.
⇒  x = -1/4π + k • 2π  ∨  3x = 11/4π + k • 2π.
⇒  x = -1/4π + k • 2π ∨  x = 5/12π + k • 2/3π.
In [0, 2π] geeft dat de oplossingen  5/12π,  13/12π,  21/12π  en  5/4π.		  
   
Voorbeeld 2.  Los  op  in [0, 2π]:  cos(x - 1/3π) = sin(1/2x)
Uit bovenstaande theorie hebben we een manier gevonden om sinus in cosinus te veranderen:   sin(α) = cos(1/2π - α)
Dat geeft hier:  cos(x - 1/3π) = cos(1/2π - 1/2x)
⇒  x - 1/3π = 1/2π - 1/2x  + k • 2π  ∨   x - 1/3π = 2π - (1/2π - 1/2x) + k • 2π 
⇒  11/2x = 5/6π + k • 2π ∨  1/2x = 11/6π + k • 2π 
⇒  x = 5/9π + k • 4/3π  ∨  x = 22/6π + k • 4π
Binnen [0, 2π] geeft dat de oplossingen  5/9π en 17/9π.
   
OPGAVEN
 
1. Leid formules af voor:
               
  a. sin(π + x)

-sinx
d. sin(1/2π + x)

cosx
 
  b. cos(-x)

cosx
e. cos(π + x)

-cosx
 
  c. sin(11/2π + x)

-cosx
f. cos(11/2π - x)

-sinx
 
        .      
2. Los algebraďsch op in [0, 2π]:
               
  a. sin(x + 1/6π) = cosx

-1/6π, 7/6π
  b. cos(2x) + sinx = 0

1/2π,7/6π, 11/6π
  c. 4cos(π - x) + 3 = 2cosx 

1/3π, 12/3π
  d. sin(1/2π + x) =  cos2x

0,1/2π,11/2π,2π
  e. sinx = cos(x + 1/3π)

1/12π,  11/12π
  f. cosx = sin(x - 1/6π)

1/3π, 11/3π
  g. cos(3x + π) = sin(x - 1/2π)

0,1/2π,π,
11/2π, 2π
  h. sin(3x) = cos(2x)

-1/10π,1/2π, 9/10π,1310π,17/10π
               
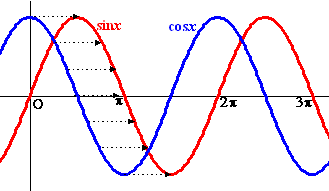
3. Ook uit de grafieken van cosx en sinx kun je formules afleiden. Kijk maar naar de twee grafieken hieronder.
               
 

               
  Je kunt de rode grafiek krijgen door de blauwe 1/2π naar rechts te schuiven.
Of je krijgt de blauwe door de rode 1/2π  naar links te schuiven
               
  Welke twee formules volgen daaruit?
           

sinx = cos(x - 1/2π)
cosx = sin(x + 1/2π)

4. We onderzoeken in deze opgave de vergelijking  sin(x + p) = cos(x - p)
               
  a. Toon aan dat deze vergelijking voor p = 1/4π voor elke x klopt.
               
  b. Toon aan dat x = 1/4π  altijd een oplossing van deze vergelijking is.
               
  c. Welke x-waarde (tussen 0 en 2π)  is nog meer altijd een oplossing van deze vergelijking?
           

x =11/4π
5. Geef alle oplossingen van  sin(2x + p) = cos(x + p)
           

x = 11/2π
x = -2/3π + 1/6π
               
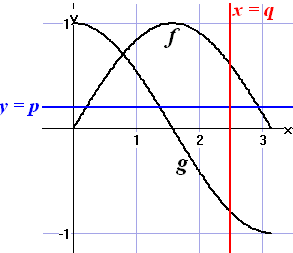
6. Gegeven zijn de functies  f(x) = sin x  en  g(x) = cos x, beiden met domein  [0,π].
De lijn met vergelijking y = p snijdt de grafiek van f in de punten A en B.
           
  a. Bereken p als AB = 2/3π
         

0,259
  b. Bereken AB in twee decimalen nauwkeurig als p = 0,3
         

0,96
  De lijn met vergelijking x = q snijdt de grafiek van  f  in het punt C en de grafiek van g in het punt D.
               
  c. Bereken q als het midden van lijnstuk CD op de x-as ligt
           

q = 3/4π
             

© h.hofstede (h.hofstede@hogeland.nl)