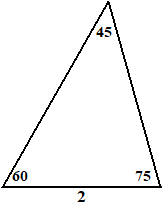© h.hofstede (h.hofstede@hogeland.nl)

Drie speciale driehoeken.
       
In de afgelopen lessen heb je intussen al aardig veel geleerd over het berekenen van lengtes en hoeken in driehoeken (en daarmee ook in andere figuren). Helaas kreeg je daarbij vaak afgeronde antwoorden, vooral door het gebruik van sinus, cosinus en tangens.  Brr..... lelijk.....!

Dat is in deze les afgelopen!

Er zijn drie speciale driehoeken waarvan de hoeken en lengtes exact te berekenen zijn, en die komen deze les aan de orde. Kortom:  doe de rekenmachine maar weg, we gaan lekker alles weer exact berekenen.

Het gaat hier om de volgende drie driehoeken.

       
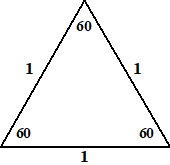
60 - 60 - 60
       
Een driehoek met alle hoeken 60º heet een gelijkzijdige driehoek.
Alle zijden zijn even lang.

Veel meer valt er eigenlijk  niet over te vertellen.

 

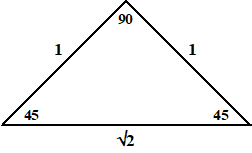
45 - 45 - 90
       
Dat heet ook wel een gelijkbenige rechthoekige driehoek. Je geo-driehoek is er een mooi voorbeeld van.
Als je de rechthoekszijden lengte x geeft, dan geldt voor de schuine zijde  s:
s2 = x2 + x2
s2 = 2x2
s =  √(2x2) = x√2

Kortom:  de zijden hebben verhouding  1 - 1 - √2

       
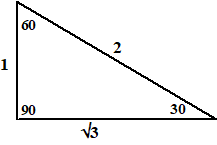
30 - 60 - 90  
       
Dit is eigenlijk de helft van een gelijkzijdige driehoek (teken hem er maar onder gespiegeld tegenaan en je hebt een gelijkzijdige driehoek).  Dat betekent dat de schuine zijde dubbel zo groot is als die ene rechthoekszijde.

Noem de kleinste rechthoekszijde x, dan is de schuine zijde dus 2x.
Noem de andere rechthoekszijde r, dan geeft Pythagoras:
x2 + r2 = (2x)2
x2 + r2 = 4x2
r2 = 3x2
r = √(3x2) = x√3

Kortom:  de zijden hebben verhouding  1 - 2 - √3

       
Met deze verhoudingen kun je dus nu de zijden altijd exact geven, dus hoef je niet af te ronden!
Misschien is het wel handig als je nog even deze les over het vereenvoudigen van wortels bekijkt.

Voorbeeld.

 

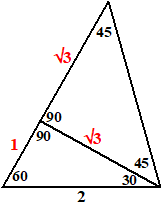
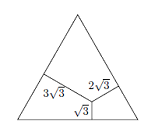
Bereken de oppervlakte van de driehoek hiernaast. Geef je antwoord exact (dus niet afgerond)

 

       
Door de hoogtelijn hiernaast te tekenen zie je dat je te maken hebt met twee driehoeken die hierboven staan beschreven.

Dat betekent dat de rode zijden de lengtes hebben zoals is aangegeven.

De oppervlakte is dan  0,5 • (1 + √3) • √3
Dat is dus gelijk aan  0,5√3 + 1,5

       
  OPGAVEN
       
1. Driehoek BCD heeft een hoek van 75º en een hoek van 45º
BD wordt verlengd tot BE, en CD tot CA, zodanig dat AE en BE loodrecht op elkaar staan, en dat bovendien geldt  AE = BE.

BC = 8

Bereken exact de oppervlakte van driehoek ABE.

     

48
2. In  een parallellogram ABCD met AD = 12 worden vanuit de punten B en D loodlijnen op de tegenoverstaande zijden getekend.

Daardoor ontstaat een vierkant BEDF.

Bereken exact de zijde AB.
     

 12√3 - 12
3. In vierkant ABCD wordt een gelijkzijdige driehoek DEC getekend.

AE wordt verlengd, en vanuit punt C wordt de loodlijn CF op AE getekend.

Deze loodlijn heeft lengte 6.

Bereken exact de oppervlakte van het vierkant.

     

 72
4. Kangoeroewedstrijd.

In een rechthoekige driehoek verdeelt de bissectrice van een scherpe hoek de overstaande zijde in 2 stukken. Eén stuk heeft lengte 1, het andere stuk heeft lengte 2.

Wat is de lengte van de bissectrice?

     

 2
5. Kangoeroewedstrijd.

Twee cirkels hebben beide straal 1.
De middelpunten van de cirkels liggen op een diagonaal ven een vierkant.
De cirkels raken elkaar en het vierkant.
Hoe groot is de zijde van het vierkant?

     

 2 + √2
6. Kangoeroewedstrijd.

Twee vierkanten met zijden 1 hebben een hoekpunt gemeen en een zijde van een van de vierkanten ligt op een diagonaal van het andere. Zie de figuur.
Wat is de oppervlakte van het gele gebied?

     

 √2 - 1
7. Kangoeroewedstrijd.

Twee cirkels met middelpunten C en D snijden elkaar in de punten A en B. De getekende hoek bij C is 600, de hoek bij D is 900.

Hoe verhouden de oppervlaktes van de cirkels zich?

     

 1 : 2
8. Kangoeroewedstrijd.

Sietse heeft een rechthoek waarvan de korte zijde √3 is. Als hij twee tegenover elkaar liggende hoekpunten naar het midden van de rechthoek vouwt, blijkt er een ruit te ontstaan: KLMN.

Wat is de oppervlakte van die ruit?

     

 2√3
9. Kangoeroewedstrijd.

In de tekening zie je een cirkelsector. De hoek van de sector is 60º en de straal is 12.
Wat is de straal van de kleine cirkel die precies in de sector past?

     

 4
10. Vlaamse Olympiade.

De onderstaande boom van Pythagoras is opgebouwd uit vierkanten en gelijkbenige rechthoekige driehoeken.
       
 

       
  Als AB = 1, waaraan is dan de oppervlakte van de gekleurde zevenhoek gelijk?
     

 15/16
11. Vlaamse Olympiade.

In deze veelhoek zijn alle zijden gelijk aan 1, en  α = 120° en  β = 60°.
De overige hoeken zijn, hetzij als binnenhoek, hetzij als buitenhoek, gelijk aan 150°

Hoe groot is de oppervlakte?
 

     

 4 + 2,5√3
12. Vlaamse Olympiade.

In een gelijkzijdige driehoek trekt men vanuit een punt binnen die driehoek de drie loodlijnen op de zijden.
De afstanden van dat punt tot de zijden zijn  √3, 2√3 en  3√3

Hoe groot is de zijde van die driehoek?

       
13. A is een gelijkzijdige driehoek en B is een vierkant met dezelfde zijden als de driehoek.

Het vierkant wordt tegen de driehoek gelegd zoals in de figuur hiernaast.

Om de hele figuur wordt vervolgens een rechthoek gezet.

De breedte van de rechthoek is 4

Bereken exact  de hoogte van de rechthoek.

       
14.

       
  ABC is een rechthoekige gelijkbenige driehoek met rechte hoek C

Met middelpunten A en B worden twee cirkels getekend die elkaar raken.

Met middelpunt C wordt vervolgens een kleinere cirkel getekend die beide andere cirkels raakt.
Die kleinere cirkel heeft straal 4

Bereken de oppervlakte van de driehoek.
       
15. ABC is een driehoek met alle zijden gelijk aan 10.

Vanuit punt P op zijde AB wordt een lijnstuk PS getekend dat  loodrecht op AC staat.
Vervolgens wordt met zijde PS een rechthoek PQRS getekend waarvan alle hoekpunten op de zijden van ABC liggen (zie de tekening)
De oppervlakte van PQRS is gelijk aan 8√3

Bereken exact de lengte van AP.

       
       
     
       

© h.hofstede (h.hofstede@hogeland.nl)