| |
 |
|
De Decibel-eenheid. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
|
De Decibel is de eenheid voor
geluidssterkte.
Nou is geluid natuurkundig gezien eigenlijk gewoon een hoeveelheid
energie die per seconde ons oor ingaat. Het is immers niets anders dan
trillende lucht. Die energie per seconde wordt in de natuurkunde meestal
uitgedrukt met de eenheid Watt.
Maar als een geluidgolf op ons oor valt, dan is de totale hoeveelheid
Watt die ons oor binnenkomt natuurlijk ook afhankelijk van de
oppervlakte van ons oor.
Het gaat bij geluidssterkte (er wordt meestal de letter I voor gebruikt)
daarom om de hoeveelheid Watt per oppervlakte-eenheid. Ofwel:|
| |
| geluidssterkte = I =
W/m2 |
|
| |
|
|
Maar er is één probleem met de hoeveelheid energie die ons oor kan
horen: dat varieert nogal!
De gehoordrempel, (dat is de kleinste hoeveelheid geluid die we normaal
gesproken kunnen waarnemen), ligt ongeveer bij 10-12 W/m2
en de pijngrens van ons oor ligt ongeveer bij 102
W/m2
Wauw! Dat is een verschil van maar liefst 14 machten van 10!!!!
Dat vraagt om een logaritmische schaal, vind je niet?
Nou nee, eigenlijk schrééuwt dit om een logaritmische schaal.
(schreeuwt natuurlijk met veel decibels, hahahahahaha)
En die logaritmische schaal die is dan ook gemaakt. De hoeveelheid
geluid wordt daarbij uitgedrukt in decibel.
Men heeft de gehoorgrens gesteld op I0 = 10-12 W/m2
Voor het aantal decibel (D) van een geluid met
intensiteit I geldt dan: |
| |
|
|
|
|
|
|
| |
|
|
|
|
Denk erom dat de log in deze
formule gelijk is aan 10log.
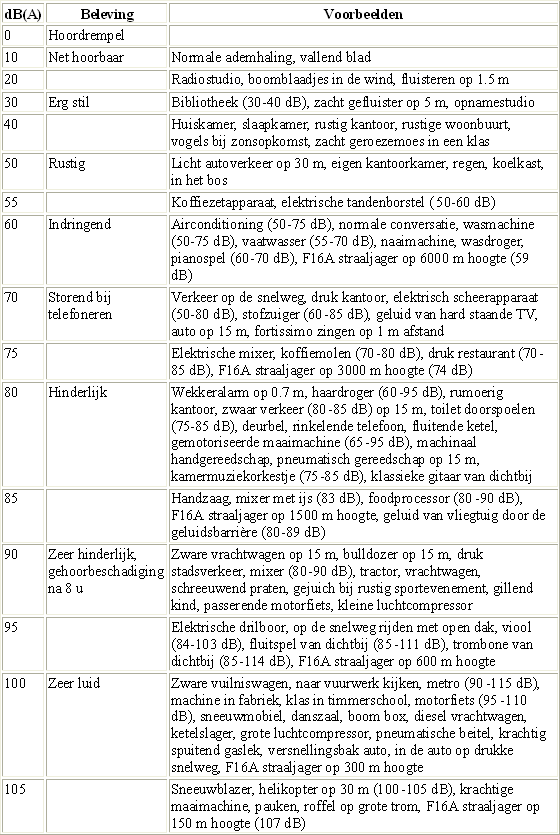
Hier zie je een decibel-tabel met
een aantal veel voorkomende gevallen: |
| |
|
|
|
|
|
 |
| |
|
|
|
|
Geluiden combineren
Als er meerdere geluiden tegelijk klinken, dan moet je natuurkundig
gezien de energie daarvan bij elkaar optellen.
Dat betekent in bovenstaande formule dat je de I' s bij elkaar
moet optellen.
| |
| Geluiden optellen
⇒
tel de
I-waarden op |
|
Je mag niet gewoon de decibellen optellen, dat zullen de volgende
voorbeelden wel duidelijk maken.
Voorbeeld 1.
Je hoort tegelijk een grasmaaier met I = 10-5 W/m2
en een rijdende vrachtwagen van I = 10-4 W/m2.
Hoeveel decibel hoor je? |
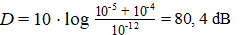 |
| |
|
|
|
|
Voorbeeld 2.
Je hoort tegelijk drie brommers met elk een geluidsniveau van 75dB
voorbijkomen.
Hoeveel decibel hoor je?
Voor één brommer geldt: |
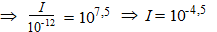 |
| Dan geldt voor drie brommer dat I
= 3 • 10-4,5 |
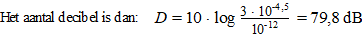 |
| |
|
|
|
|
| |
|
|
|
|
| 1. |
Een operazangeres produceert 50 dB geluid.
Hoeveel decibel wordt dat samen, als ze een duet zingt met een
operazanger die 55 dB produceert? |
| |
|
|
|
|
| 2. |
De leden van het Shantykoor "Zeegeluiden"
produceren elk een geluidsniveau van 40 dB. |
| |
|
|
|
|
| |
a. |
Als het hele koor uit 60 leden
bestaat, hoeveel dB produceert dat hele koor dan? |
| |
|
|
|
|
| |
b. |
Uit hoeveel leden zou het koor
moeten bestaan om 75 dB geluid te produceren? |
| |
|
|
|
|
| |
|
| 3. |
Wat weet je van de
geluidsintensiteitsverandering als het aantal decibel 3 groter
wordt? |
| |
|
| 4. |
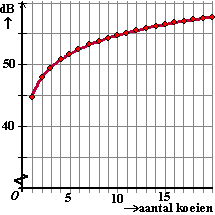
Hiernaast staat een
grafiek van de hoeveelheid decibel (D) in een stal als functie
van het aantal koeien (k)
Het blijkt dat één koe, als hij loeit, lawaai van 50 dB
produceert. |
 |
| |
|
|
| |
a. |
Met hoeveel decibel zal het
geluidsniveau in de stal toenemen als er zes koeien extra
loeien? |
| |
|
|
|
|
| |
Al je de decibellen voor 11 koeien
samen berekent, dan kom je uit op 60,4 decibel. Maar dat klopt
niet met de gegeven grafiek! Dat komt natuurlijk omdat een koe
niet de hele tijd aan het loeien is. |
| |
|
|
|
|
| |
b. |
Bepaal met behulp van de grafiek
hoeveel procent van de tijd een koe ongeveer loeit. |
| |
|
|
|
|
| |
|
|
|
|
|
|
De afstand tot de geluidsbron. |
| |
|
|
|
| Nou is er in het bovenstaande
verhaal één ding voor het gemak steeds achterwege gelaten: hoe hard iets klinkt
hangt natuurlijk af van hoe ver je er vanaf bent. Laten we beredeneren
hoe de geluidssterkte afhangt van de afstand tot de geluidsbron. |
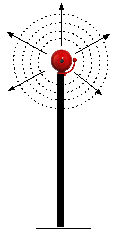
Een vrijstaande geluidsbron stuurt het geluid (zijn energie dus) alle
kanten op. Een geluidsgolf die begint bij de bron gaat dus alle kanten
op, en dat ziet eruit als een bol die steeds groter wordt.
Maar de oorspronkelijke energie van die golf wordt dus verdeeld over het
hele oppervlakte van de bol.
Omdat de oppervlakte van een bol gelijk is aan 4πr2
zal de intensiteit van het geluid dus gedeeld moeten worden door
4πr2 . Ofwel:
| |
| de intensiteit is evenredig met
1/r2
|
|
| |
Dat betekent bijvoorbeeld dat, als je 3 keer zo ver van een
geluidsbron af gaat staan, dat dan de intensiteit 9 keer zo klein wordt. |
 |
| |
|
|
|
|
| |
|
|
|
|
| 5. |
Ik sta op 2 meter afstand van de geluidsbox bij
een popconcert, en ik hoor een geluidsintensiteit van naar
schatting 130 dB. Dat is maar liefst 10 dB boven wat meestal
gezien wordt als de pijngrens. Het doet ook behoorlijk zeer en
ik besluit daarom verder van de box af te gaan staan.
Hoe ver moet ik van de geluidsbox gaan staan zodat de
geluidsintensiteit gelijk wordt aan 110 dB? |
| |
|
|
|
|
| |
|
|
|
|
| 6. |
Twee geluidsbronnen staan 20 meter van elkaar
af. Zij produceren op 1 meter afstand een aantal decibel van 30
en 40. Onderzoek met je GR waar tussen deze twee bronnen in je
je moet bevinden om zo min mogelijk geluid te horen. |
| |
|
|
|
|
| |
|
|
|
|
| 7. |
De
hoeveelheid decibel (dB) die een vrachtwagen produceert is
afhankelijk van de geluidsenergie I die hij levert volgens de
formule: dB = 10 · log(I · 1012). |
| |
|
|
|
|
| |
a |
Hoeveel energie produceert een vrachtwagen die een lawaai van 95
dB produceert? |
| |
|
|
|
|
| |
b. |
Hoeveel vrachtwagens van 95 dB zijn er nodig om onze pijngrens
(140 dB) te bereiken? |
| |
|
|
|
|
| |
Natuurlijk is het aantal decibel afhankelijk van de afstand tot
de vrachtwagen. Als de afstand s (in m) is, dan
blijkt dB voor s groter dan één meter omgekeerd evenredig
met s2 te zijn. De volgende tabel geeft een
aantal metingen aan één lawaaibron: |
| |
|
|
|
|
| |
|
Afstand s (in m) |
2,3 |
4,7 |
9,1 |
12,1 |
|
Geluidssterkte (in dB) |
2,36 |
0,56 |
0,15 |
0,09 |
|
| |
|
|
|
|
| |
c. |
Leg uit waarom dit verband niet kan gelden voor s = 0 |
| |
|
|
|
|
| |
d. |
Stel een formule op voor dB als functie van s. |
| |
|
|
|
|
| |
|
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
|