d'Alembert en Cauchy

© h.hofstede (h.hofstede@hogeland.nl)

Twee speciale convergentiekenmerken.

Stel er is een rij u_nwaar een somrij van gemaakt wordt, met oneindig veel termen.

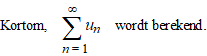Dan zijn er twee kenmerken waaraan je snel kunt zien of die som zal convergeren (naar een bepaalde grenswaarde toe gaan) of divergeren (oneindig worden, of heen en weer springen of zoiets). Deze les gaat over die twee kenmerken.

1. Het kenmerk van d' Alembert.

Het kenmerk van d'Alembert zegt het volgende:

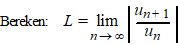Dan zijn er voor die L drie mogelijkheden:

•

L < 1. Dan convergeert de rij u_n

•

L > 1. Dan divergeert de rij u_n

•

L = 1. Dan is het onbekend....

Het bewijs.
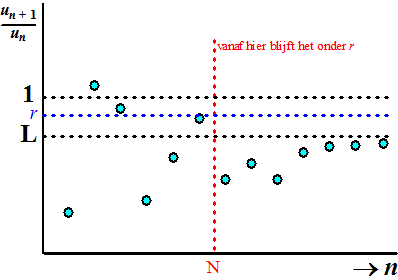
Als die rij naar L toe gaat, dan zal hij vanaf een bepaalde n daar heel dicht bij gaan zitten.

Als L < 1 dan zul je vanaf bepaalde n dus best een getal r tussen L en 1 in kunnen vinden.

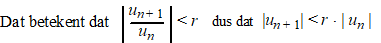
Stel dat dat gebeurt vanaf n = N.
Dan kunnen we een rijtje maken (uit luiheid laat ik de absolute waarde strepen even weg):

u_{N + 1} < r • u_Nu_{N + 2} < r • u_{N + 1} < r² • u_Nu_{N + 3} < r • u_{N + 2} < r³ • u_N
u_{N + 4} < r • u_{N + 3} < r⁴ • u_{N

.........}

Komt je al bekend voor?
Daar staat een rij positieve getallen u_{N+ 1}, u_{N + 2}, u_{N + 3}, ... die kleiner zijn dan de getallen u_N, ru_N, r² u_N, r³ u_N, ...
Maar die laatste rij is een oude bekende: een meetkundige rij met reden r < 1 en beginwaarde u_N
Daarvan is bekend dat die convergeert (naar nul). Dus onze rij u_n vanaf de waarde N ook.
Tel daar alle waarden van u_n vóór N bij op, en het convergeert nog steeds (je telt er alleen een constant eindig getal bij op).

Als L > 1 dan zal vanaf bepaalde N juist gelden dat ½u_{N + 1}½ > ½u_N ½ dus de u_n-waarden zullen steeds groter worden, en dus zeker niet naar nul gaan. Maar dat moet voor convergentie wel!
Dat kun je zó zien door u_n als verschil van twee sommen te bekijken:

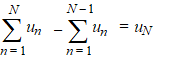Dat klopt want de ene u_N is net degene die er bij is gekomen tussen beide sommen.
Maar als N groot genoeg is, en de rij convergeert dan zullen die beide sommen aan de linkerkant gelijk worden, dus moet u_N wel naar nul gaan. Omdat voor L > 1 de u_n steeds groter wordt kan hij niet naar nul gaan dus de rij zal niet convergeren, (dus divergeren).

Voorbeeld.

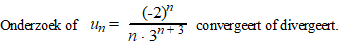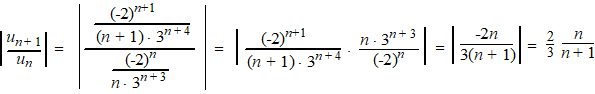voor n naar oneindig gaat die breuk ⁿ/_{(n + 1)} naar 1, dus de rechterkant gaat naar ²/₃.
Dat is kleiner dan 1, dus de rij convergeert.

2. Het kenmerk van Cauchy.

Ook Cauchy kwam met een kenmerk om convergentie te onderzoeken. Dat luidt als volgt:

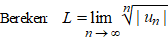Dan zijn er voor die L drie mogelijkheden:

•

L < 1. Dan convergeert de rij u_n

•

L > 1. Dan divergeert de rij u_n

•

L = 1. Dan is het onbekend....

Het bewijs.
Gaat bijna hetzelfde als bij d'Alembert, daarom geef ik het wat beknopter.
Neem eerst L < 1. Kies weer zo'n r tussen L en 1 in, dan geldt: ½u_n½^1/n < r dus ½u_n½< rⁿ
Maar daar staat alweer zo'n meetkundige rij die voor r < 1 naar nul gaat, maak het verhaal zelf maar verder af....

Voorbeeld.

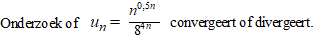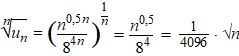Dat laatste gaat voor n naar oneindig zelf ook naar oneindig, dus de rij divergeert.

Tipje voordat de opgaven beginnen.
Bij onderzoek met het kenmerk van Cauchy is het vaak handig om de volgende limiet te weten:

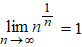Onderzoek met het kenmerk van d'Alembert of de volgende rijen convergeren of divergeren.

convergent

divergent

Onderzoek met het kenmerk van Cauchy of de volgende rijen convergeren of divergeren.

divergent

convergent

Stel dat je bij het kenmerk van d'Alembert vindt dat L = 1. Dan werkt die methode dus niet.
Toon aan dat het in dat geval geen zin heeft te proberen of het kenmerk van Cauchy misschien wél wat oplevert.

Toon aan dat, als een rij u_n convergeert dat dan de rij n • u_n ook convergeert.

Gegeven is de rij a + b + a² + b² + a³ + b³ + ... met 0 < a < b < 1
Leg uit waarom het kenmerk van d'Alembert niet werkt bij deze rij.