|
|
 |
|
De cosinusregel. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
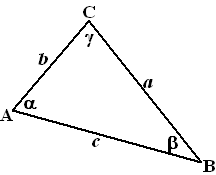
Hiernaast zie je nog een keer de
afspraken over naamgeving in een driehoek. Voor de hoekpunten gebruiken
we hoofdletters, voor de zijden kleine letters en voor de hoeken Griekse
letters.
Met de stelling van Pythagoras, en met sos-cas-toa en met de sinusregel
kun je intussen al heel wat driehoeken "berekenen".
Maar er zijn twee gevallen waarbij zelfs die mooie sinusregel niet
werkt.
Hier zijn daar twee voorbeelden van: |
 |
| |
|
|
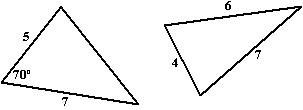 |
Zie je al dat het niet wil met de sinusregel?
Dat komt natuurlijk omdat je in deze twee gevallen nergens een hoek en
de bijbehorende zijde ertegenover weet.
Irritant hé? |
| |
|
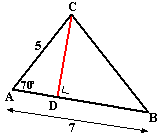
En toch kunnen we met wat kunst- en vliegwerk
toch de andere hoeken en zijden van deze driehoeken berekenen.
Neem de linkerfiguur. Hiernaast is daar een hoogtelijn CD bij
ingetekend.
In driehoek ADC geldt dan cos70º = AD/5
dus AD = 5 • cos70º
Pythagoras geeft dan: AD2 + CD2 = AC2
ofwel (5 • cos70º)2 + CD2 = 52
⇒ CD2
= 25 - 25 • (cos70º)2
Nu schakelen we over naar driehoek CDB. |
 |
| DB = AB AD = 7
- 5 • cos70º |
|
En dan komt onze goede oude
vriend Pythagoras ons weer helpen: DB2 + CD2
= BC2
Dat geeft met de gegevens hierboven: (7
- 5 • cos70º)2
+ 25 - 25 • (cos70º)2 = BC2
Haakjes wegwerken: 49 - 70cos70º + 25(cos70º)2 +
25 - 25(cos70º)2 = BC2
Hé! Leuk!!
Die stukken met (cos70º)2 vallen tegen elkaar weg!!!
Dan blijft over BC2 = 49 + 25
- 70 • cos70º
Intoetsen geeft BC2 ≈
50,05 dus BC ≈ 7,07.
Gelukt! |
| |
|
Die hele berekening kun je natuurlijk ook met
letters doen. Vervang overal de 5 door b en de 7 door c
en de 70º door
α. Als je de berekening dan
nog een keer opschrijft dan geeft dat de volgende prachtige formule:
| |
|
a2
= b2 + c2
- 2bc • cosα |
|
| |
|
 |
| Deze formule heet de cosinusregel.
|
|
| |
|
| 1. |
Leid zelf de cosinusregel volgens het voorbeeld hierboven
af. |
| |
|
|
De cosinusregel ziet er misschien wat
ingewikkeld uit, maar valt erg mee als je je maar bedenkt dat die twee
letters b en c aan de rechterkant in willekeurige volgorde
staan. Het enige waar je aan moet denken is, dat de hoek
α tegenover de zijde a moet liggen.
Dus: de zijde aan de linkerkant ligt tegenover de hoek.
Bij berekeningen in driehoeken zou ik daarom eerst kijken welke hoek ik
wil gebruiken of berekenen en die dan
α
noemen. Dan is de zijde daartegenover automatisch zijde a en zijn
de andere twee b en c. |
 |
Waarschuwing.
Denk er goed om dat deze formule algebraïsch gezien eigenlijk bestaat
uit 4 stukken. |
 |
|
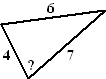 |
Als je bijvoorbeeld van de driehoek hiernaast
de hoek met het vraagteken wilt berekenen, dan begin je met de
zijde ertegenover. Dat geeft: 62 = 42
+ 72 - 2 • 4 • 7 • cosα
Dus: 36 = 16 + 49 - 56 • cosα.
Maar nu kun je niet eerst 16 + 49
- 56 uitrekenen!!!!
Die 56 zit namelijk vast aan de cosα.
De goede manier is om eerst de stukken 16 en 49 naar de andere
kant te brengen en daarna te delen door die -56.
zo dus: |
|
| 36 = 16 + 49
- 56 • cosα |
| ⇒ |
36 - 16
- 49 = -56 • cosα |
| ⇒ |
-29 = -56 • cosα |
| ⇒
|
-29/-56 = cosα |
| ⇒
|
α = cos-1(-29/-56)
≈ 58,8º |
|
| |
|
Geruststelling:
Je hoeft er bij de cosinusregel niet op te letten of de hoeken stomp of
scherp zijn (zoals bij de sinusregel wel nodig was)
De functie cos-1x geeft een hoek tussen 0º en
180º dus die doet de stompe hoeken vanzelf goed. |
| |
|
|
OPGAVEN |
| |
|
|
|
| 8. |
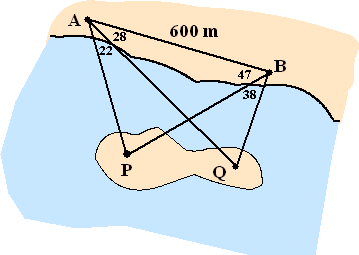
Voor de kust ligt een eiland met
daarop twee kerktorens: één bij P en één bij Q. Iemand wil graag
de afstand tussen beide torens bepalen.
Zij doet dat door vanaf twee punten A en B aan de oever de
hoeken die hiernaast staan aangegeven te meten.
Verder meet zij de afstand AB = 600 meter.Bereken de afstand
tussen beide torens op het eiland.
|
 |
| |
|
|
| |
|
|
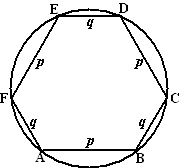
 9. 9. |
Een zeshoek heeft zijden met lengtes p
en q.
Om-en-om.
Als R de straal is van de omgeschreven cirkel van deze zeshoek,
dan geldt:
R2 =
1/3(p2
+ pq + q2)
Toon dat aan.
Gebruik daarbij het feit dat driehoek FDB in de figuur hiernaast
gelijkzijdig is. |
 |
| |
|
|
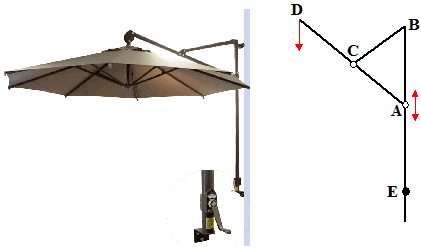
| 10. |
Hiernaast zie je een afbeelding van een
muurparasol "Tenerife" van de firma Garden Impressions (€250,-).
Helemaal onderaan in punt E zit een molentje waarmee je een
staalkabeltje (dat door stang AE loopt) kunt opwinden waardoor
punt A naar beneden wordt getrokken langs stang BE
Als je het molentje weer "afwindt" zal door het gewicht van de
parasol punt A weer omhoog gaan.
C is een vast punt waar BC scharnierend aan AD vastzit. |
 |
| |
De afmetingen zijn BE = 120, BC =
30, CD = 50, AC = 40. Alles in cm.
Stel dat AB = x
Dan geldt voor de verticale afstand (h) tussen D en
E: h = 120 + 1/8x + 787,5/x |
| |
|
|
| |
| a. |
Toon dat aan. |
| |
|
| b. |
Laat zien dat vanaf ingeklapte toestand (x =
70) punt D alleen maar stijgt als x afneemt (dus
als A omhoog gaat). |
|
| |
|
|
 |
|
| |
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|