cilindercoordinaten

© h.hofstede (h.hofstede@hogeland.nl)

Cilindercoördinaten.

Eerst even een superkorte herhaling van poolcoördinaten, waant daar lijkt deze les nogal verdacht veel op.
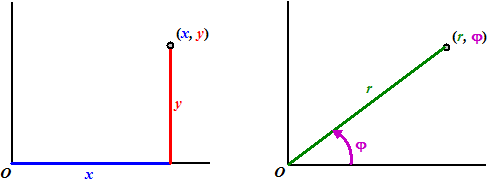
Poolcoördinaten was een andere manier om de plaats van een punt in een vlak aan te geven. Niet zoals "gewoonlijk" met een x-coördinaat en een y-coördinaat, maar met en r-coördinaat en een φ-coördinaat, waarbij r de afstand tot de oorsprong is, en j de hoek met de positieve x-as. Dat ziet er zó uit:

Vooral als het ging om problemen met cirkelvormen erin dan was het vaak handig om poolcoördinaten te gebruiken in plaats van "gewone" (rechthoekige) coördinaten.

Wanneer het gaat om ruimtecoördinaten waarvan één van de drie aanzichten ook cirkelvormen bevat, dan werken zogenaamde "cilindercoördinaten" soms handiger dan rechthoekige coördinaten.
Dat ziet er zó uit:

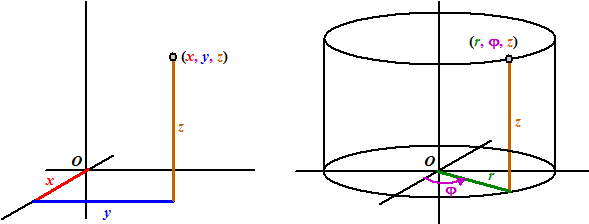Daar in de bodem gebruiken we gewoon poolcoördinaten, alleen is er nu een z-coördinaat aan toegevoegd om een derde dimensie te krijgen.
Ik hoop dat je direct ziet dat het verband tussen rechthoekige coördinaten en cilindercoördinaten is:

x = rcosφ, y = rsinφ en z = z

en andersom:

r² = x² + y² , φ = arctan(^y/_x) en z = z

Die φ is een eikeltje:
Kijk wel goed uit of de arctan-functie wel de goede waarde van φ geeft). De standaard arctan-functie geeft namelijk altijd een waarde tussen -¹/₂π en ¹/₂π dus soms moet je er nog π bij optellen om de goede φ te krijgen! Maak een schets!
Verder kun je natuurlijk die φ nog kiezen plus of min een aantal keer 2π.

Cilindercoördinaten werken vooral erg handig als het gaat om problemen met een as van symmetrie (die we dan uiteraard als z-as nemen). Zo is de vergelijking van de cilindermantel in rechthoekige coördinaten gelijk aan x²+y² =c² maar in cilindercoördinaten is die vergelijking veel eenvoudiger: r = c, that's all!!

En de dubbele kegelmantel hiernaast met als as de z-as heeft in rechthoekige coördinaten de vergelijking x² + y² = z²
Maar in cilindercoördinaten is het gewoon z = ± r
Een stuk makkelijker.


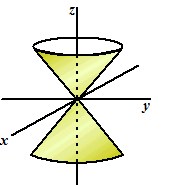1.	Verander de coördinaten van de volgende punten van rechthoekige naar cilindercoördinaten. Rond indien nodig de hoeken af op twee decimalen.

	a.	A = (2, -4, 6)

	b.	B = (1, 1, 1)

	c.	C = (3, 4, -2)

2.	Verander de coördinaten van de volgende punten van rechthoekige naar cilindercoördinaten:

	a.	A = (2, ²/₃π, 1)

	b.	B = (1, ⁵/₄π, 4)

	c.	C = (6, ¹/₂π, -6)

3.	Schets de vlakken met de gegeven vergelijking in cilindercoördinaten:

	a.	φ = ¹/₄π

	b.	r = 5

	c.	z = 9 - r²

Integralen met cilindercoördinaten.

Als je vermoedt dat je een drievoudige integraal makkelijk met cilindercoördinaten kunt oplossen (omdat de figuur de z-as als symmetrieas heeft), integreer dan éérst over z. Dan houd je daarna nog het bovenaanzicht over, en dat is een integraal over r en j over, en die kun je net zo berekenen als we al met poolcoördinaten deden.
Denk om de Jacobiaan: dx • dy = r • dr • dφ

Integreren met cilindercoördinaten:
•	integreer éérst over z.
•	integreer dan het bovenaanzicht met poolcoördinaten: dx • dy = r • dr • dφ

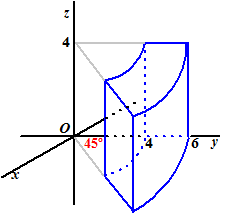
Voorbeeld.
Bereken de integraal van de functie f(x, y, z) = z • (x² +y²)over het blauwe lichaam hiernaast.

z loopt van 0 tot 4

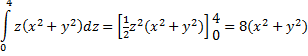En nu houden we in het bovenaanzicht een integraal over voor r van 4 tot 6 en φ van ¹/₄π tot ¹/₂π van de functie 8r² :

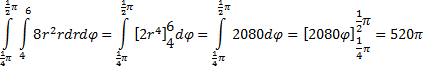Nou, zo werkt dat dus.....


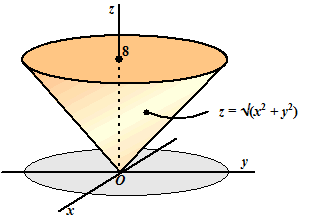
4.	Bereken de integraal van f(x, y, z) = 2z over de gekleurde kegel hiernaast. (de kegelmantel heeft zoals je in de figuur ziet vergelijking z = √(x² + y²) en loopt van z = 0 tot z = 8)