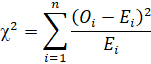© h.hofstede (h.hofstede@hogeland.nl)

De χ-kwadraat verdeling.
       
De χ2 verdeling (spreek uit  "chi-kwadraat")  is één van de meest gebruikte en misbruikte verdelingen in de statistiek. Waarschijnlijk komt dat omdat deze verdeling makkelijk en op meerdere gebieden toe te passen is.
Officieel is de χ2 verdeling gedefinieerd als:
       

De χ2 verdeling met n vrijheidsgraden is de verdeling van de kwadraten
van n onafhankelijke standaardnormaal-verdeelde variabelen. 

       
Ofwel simpeler gezegd:  "Als variabelen normaal verdeeld zijn, dan zijn hun kwadraten χ2-verdeeld".

We zullen de komende lessen een aantal verschillende toepassingen van de χ2 verdeling zien:
       
1. De kwaliteit van een fit.
2. Het testen van een verdeling.
3. Een test voor onafhankelijkheid.
       
Zoals je ziet:  een echt manusje van alles!

De kwaliteit van een fit.
       
Bij  een onderzoek naar obesitas (zwaar overgewicht) onder de jeugd werden er 400 kinderen bekeken en daarbij werden er 124 gevallen van obesitas gevonden. Dat is maar liefst 31%.
De volgende tabel geeft de aantallen voor vier leeftijdscategorieën:
       
leeftijd aantal kinderen aantal obesitas-gevallen (O)
6-9 145 50
9-12 80 22
12-15 110 30
15-18 65 22
totaal 400 124
       
We vragen ons af of obesitas in alle leeftijdsgroepen even vaak voorkomt, en stellen als nulhypothese:
H0:  "Obesitas komt bij alle leeftijden even vaak voor".
Hoe goed passen de gegevens uit deze tabel bij deze hypothese? Ofwel:  hoe goed "fit" deze tabel met H0?

We breiden de tabel daarvoor uit met de verwachte aantallen obesitas (E van "Expected", en het gemeten aantal is de O van "Observed") als de kans inderdaad voor elke groep 31% is:
       
leeftijd aantal kinderen gemeten  aantal (O) verwachte aantal (E)
6-9 145 50 44,95
9-12 80 22 24,80
12-15 110 30 34,10
15-18 65 22 20,15
totaal 400 124 124
       
Daarna berekenen we de kwadratische afwijkingen tussen O en E, en delen die door de verwachte aantallen E (om er een wegingsfactor aan te geven):
       
leeftijd aantal kinderen gemeten aantal (O) verwachte aantal (E) (O - E)²/E
6-9 145 55 44,95 2,25
9-12 80 19 24,80 1,36
12-15 110 25 34,10 2,43
15-18 65 25 20,15 1,17
totaal 400 124 124 χ2 = 7,21
       
De som van de laatste kolom geeft nu de waarde van χ2  bij 3 vrijheidsgraden. Het aantal vrijheidsgraden is altijd één minder dan het aantal metingen, omdat de metingen niet onafhankelijk zijn.  De laatste waarde 1,17 bijvoorbeeld ligt al vast als de andere drie bekend zijn, omdat het totaal vast ligt.
       

       
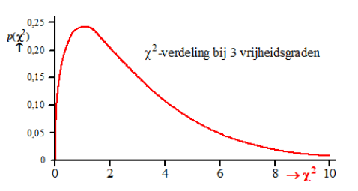
(De O staat voor "observed" en de E voor "expected").
Tot slot kijken we hoe groot de kans op een minstens even grote χ2 is. De χ2-verdeling voor 3 vrijheidsgraden zie je hieronder:
 

       
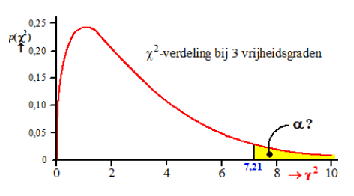
En nu is het de vraag of de overschrijdingskans (dat is de kans op een minstens even grote waarde van χ2) kleiner is dan het significantieniveau α. Ofwel:  Als α = 0,05, is de gele oppervlakte hieronder dan meer of minder dan 5%?
       

       
Er zijn uiteraard weer tabellen om bij allerlei verschillende vrijheidsgraden en significantieniveaus de grenswaarden op te zoeken. De grenswaarde bij 3 vrijheidsgraden en α = 0,05 is gelijk aan 7,81. De gele oppervlakte is kennelijk groter dan 0,05 dus we moeten concluderen dat er geen reden genoeg is om H0 te verwerpen.

Hier is de tabel met de grenswaarden voor de χ2-verdelingen.
       
significantieniveau
vrijheids-
graden		 0,250 0,100 0,050 0,025 0,010 0,005 0,001
1
2
3
4

5
6
7
8
9

10
11
12
13
14

15
16
17
18
19

20
21
22
23
24

25
26
27
28
29

30
40
50
60
70|
80
90
100		 1,32
2,77
4,11
5,39

6,63
7,84
9,04
10,2
11,4

12,5
13,7
14,8
16,0
17,1

18,2
19,4
20,5
21,6
22,7

23,8
24,9
26,0
27,1
28,2

29,3
30,4
31,5
32,6
33,7

34,8
45,6
56,3
67,0
77,6
88,1
98,6
109		 2,71
4,61
6,25
7,78

9,24
10,6
12,0
13,4
14,7

16,0
17,3
18,5
19,8
21,1

22,3
23,5
24,8
26,0
27,2

28,4
29,6
30,8
32,0
33,2

34,4
35,6
36,7
37,9
39,1

40,3
51,8
63,2
74,4
85,5
96,6
108
118		 3,84
5,99
7,81
9,49

11,1
12,6
14,1
15,5
16,9

18,3
19,7
21,0
22,4
23,7

25,0
26,3
27,6
28,9
30,1

31,4
32,7
33,9
35,2
36,4

37,7
38,9
40,1
41,3
42,6

43,8
55,8
67,5
79,1
90,5
102
113
124		 5,02
7,38
9,35
11,1

12,8
14,4
16,0
17,5
19,0

20,5
21,9
23,3
24,7
26,1

27,5
28,8
30,2
31,5
32,9

34,2
35,5
36,8
38,1
39,4

40,6
41,9
43,2
44,5
45,7

47,0
59,3
71,4
83,3
95,0
107
118
130		 6,63
9,21
11,3
13,3

15,1
16,8
18,5
20,1
21,7

23,2
24,7
26,2
27,7
29,1

30,6
32,0
33,4
34,8
36,2

37,6
38,9
40,3
41,6
43,0

44,3
45,6
47,0
48,3
49,6

50,9
63,7
76,2
88,4
100
112
124
136		 7,88
10,6
12,8
14,9

16,7
18,5
20,3
22,0
23,6

25,2
26,8
28,3
29,8
31,3

32,8
34,3
35,7
37,2
38,6

40,0
41,4
42,8
44,2
45,6

46,9
48,3
49,6
51,0
52,3

53,7
66,8
79,5
92,0
104
116
128
140		 10,8
13,8
16,3
18,5

20,5
22,5
24,3
26,1
27,9

29,6
31,3
32,9
34,5
36,1

37,7
39,3
40,8
42,3
43,8

45,3
46,8
48,3
49,7
51,2

52,6
54,1
55,5
56,9
58,3

59,7
73,4
86,7
99,6
112
125
137
149
       
Als je het graag exact wilt weten, dan heb je hier de formule voor de kansdichtheid van de chi-kwadraat verdelingen met k vrijheidsgraden:

       
Daarin is  Γ de beroemde gammafunctie waarover je in deze les meer te weten kunt komen.
       
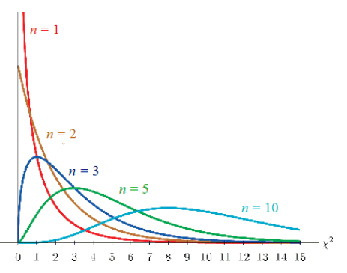
Je hebt er verder niets aan, maar hieronder staan de grafieken van de verschillende χ2-verdelingen. Nou ja.... kun je je er misschien een beetje iets bij voorstellen.....
       

       
Een binomiale toets benaderen.
       
Een onderzoeker wil kijken of snoepproducten die bij de kassa aangeboden vaker worden verkocht worden dan snoepproducten ergens anders in de winkel. Hij zet daarom twee identieke displays met snoep in de winkel:  eentje bij de kassa en eentje ergens anders.
Het blijkt dat op de eerste dag 41 snoepproducten uit het kassadisplay zijn verkocht en 27 uit het andere display.
Mag je concluderen dat de kassadisplay beter verkoopt (met α = 0,05)?

Je kunt dit makkelijk met een p-toets berekenen. Dat gaat als volgt:
H0:  "Er is geen verschil":   p = 0,5    (voor elke klant die snoep kocht was de kans voor beide displays 50%)
H1:   "Er is wél een verschil":  p ≠ 0,5  (succes = een snoepzakje uit de kassadisplay verkocht).
n = 68.  Meting was 41 successen.
P(X ≥ 41) = 1 - binomcdf(68, 0.50, 40) = 0,0571
Dat is groter dan 0,5α  (= 0,025) dus H0 aannemen:  de kassadisplay verkoopt niet significant beter.

We kunnen dit ook benaderen met een χ2-verdeling.
Omdat er maar twee metingen zijn (kassadisplay  en  andere display) is het aantal vrijheidsgraden 2 - 1 = 1.
Maar omdat de binomiale verdeling discreet is  (succes/geen succes), en de χ2-verdeling continu is,  is er ook hier een  continuïteitscorrectie nodig (net zoals bij de normale benadering van de binomiale verdeling).
Die correctie houdt in dit geval in dat de gemeten frequenties  0,5 dichter naar de verwachte frequenties moeten worden genomen.
Dat geeft deze tabel voor de χ2-verdeling:
       
verkooppunt frequentie gecorrigeerde frequentie gemiddelde bijdrage aan χ2
kassadisplay 41 40,5 34 1,24
andere display 27 27,5 34 1,24
       
χ2 = 1,24 + 1,24 = 2,48
De tabel geeft bij 1 vrijheidsgraad en α = 0,05  een kritieke waarde van 3,84
De gemeten χ2 is kleiner dan de kritieke waarde, dus H0 wordt aangenomen:  er is niet voldoende verschil om te kunnen concluderen dat de kassadisplay beter verkoopt.

één-  of tweezijdig?
Toch zou je in bovenstaand voorbeeld ook de hypothesen H0:  "er is geen verschil" en  H1: "de kassadisplay verkoopt beter" kunnen opstellen. In dat geval wordt de toets éénzijdig, en zou je bij de p-toets nu H0 noog steeds moeten aannemen (0,057 > 0,05).
De χ2 verdeling is altijd tweezijdig:  je kunt altijd alleen concluderen "of er iets aan de hand is". Kwadraten zijn immers allemaal positief, dus de χ2-verdeling heeft altijd aalleen een staart naar rechts.
Als je dan toch per se éénzijdig wilt toetsen dan moet je de kritieke waarden van de χ2-verdeling met 1 vrijheidsgraad daarop aanpassen.
De kritieke waarden worden dan: (alle significantieniveaus uit bovenstaande tabel zijn gehalveerd)
       
  significantieniveau
vrijheids-
graden		 0,125 0,050 0,025 0,0125 0,005 0,0025 0,0005
1
2
3
4

.....
 		 1,32
2,77
4,11
5,39

.....		 2,71
4,61
6,25
7,78

.....		 3,84
5,99
7,81
9,49

.....		 5,02
7,38
9,35
11,1

.....		 6,63
9,21
11,3
13,3

.....		 7,88
10,6
12,8
14,9

.....		 10,8
13,8
16,3
18,5

.....
       
De kritieke waarde voor ons voorbeeld is nu 2,71.  Nog steeds H0  aannemen.
       
       
   OPGAVEN
       
1. De volgende tabel is het resultaat van 30 worpen met een dobbelsteen.
       
 
ogen 1 2 3 4 5 6
frequentie 4 3 6 9 2 6
       
  Gebruik een χ2 test met een significantieniveau van 10% om te bepalen of je mag stellen dat dit een zuivere dobbelsteen is of niet.
       
2. Albert, Bernice en Charles spelen samen 48 keer een kansspelletje.
Albert wint er 10, Bernice wint er 24 en Charles wint er 14.
Gebruik een χ2 test met een significantieniveau van 5% om te bepalen of je mag stellen dat de kans om te winnen voor iedereen gelijk is.
     
       

© h.hofstede (h.hofstede@hogeland.nl)