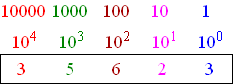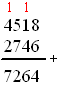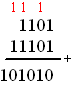tweetallig stelsel, binair


	© h.hofstede (h.hofstede@hogeland.nl)

Het tweetallig stelsel

Laten we iets eenvoudigs gaan doen: we gaan knikkers tellen!

Ik leg een aantal knikkers in het zand, en jij moet zeggen hoeveel het er zijn.
Zie de figuur hiernaast.

Wat zeg je?

Heel goed: het zijn er vier. Daar hebben we dit symbool voor: 4

Weet je wat: we maken een sommetje.
Ik leg er een aantal knikkers bij, en jij moet weer zeggen hoeveel het totaal wordt.
Zie de figuur hiernaast.

Ik hoop dat je nu vindt dat er 7 knikkers liggen, en dat we nu de som 4 + 3 = 7 hebben gemaakt.

Laten we met die 7 weer een sommetje gaan maken.
Zie de figuur hiernaast.

Tja: wordt al lastiger hè?
Als je goed telt zul je wel tot vijftien knikkers komen, want ik heb er acht bijgelegd.

En nu heb ik opeens een geweldig idee!!

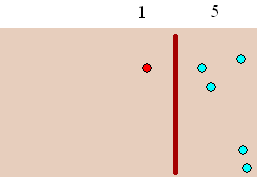
Om het jou makkelijker te maken trek ik een streep in het zand, en ik vervang tien knikkers door ééntje aan de andere kant van die streep.
Kijk: dat telt toch veel makkelijker dan die chaos hierboven....

Je moet wel even goed onthouden dat die ene rode knikker dus eigenlijk telt voor TIEN.

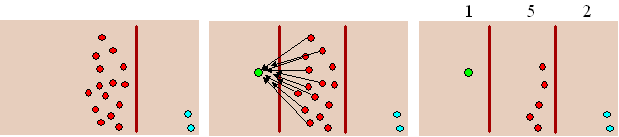
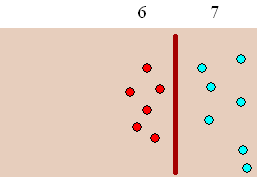
Je ziet daar boven de figuur ook trouwens al wel de cijfers 1 en 5 staan. Die 1 is van die ene rode knikker (die eigenlijk voor 10 telt) en die 5 van die 5 blauwen.

Grotere aantallen geeft ineens geen enkel probleem meer. Als ik er tweeënvijftig knikkers bij wil leggen, dan leg ik er gewoon 5 roden en 2 blauwen bij.

Dat zie je hiernaast.
Het zijn zevenenzestig knikkers geworden.

Het voordeel is dat ik nu nooit tot meer dan TIEN hoef te tellen, en daar ben ik nogal goed in, want ik heb toevallig precies TIEN vingers.

Die cijfers 6 en 7 boven de figuur geven dus zestig en zeven knikkers aan

OK tot slot: ik leg er vijfentachtig knikkers bij.
Dat zijn 8 roden en 5 blauwen.
Maar de afspraak is dat elke TIEN knikkers steeds opschuiven naar het volgende vak in het zand.
Dus TIEN van die blauwen worden 1 nieuwe rode:

Maar nu zijn er meer dan tien roden: dus maken we een nieuw vak en verschuiven tien van die roden naar 1 groene

Zo'n groene knikker telt dus voor tien maal tien is honderd!!
Die cijfers 1, 5, 2 daarboven zeggen dus dat er nu 1 • 100 plus 5 • 10 plus 2 knikkers liggen.

Op deze manier heb je, om een getal weer te geven, maar tien verschillende cijfers nodig, namelijk 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Meer knikkers kunnen er immers ergens niet liggen. De plaats in een getal zegt voor hoeveel zo'n cijfer meetelt.
Van rechts naar links voor 1, 10, 100, 1000, .....
Dat is hetzelfde als 10⁰ , 10¹, 10² , 10³ , ....

Het is vast geen toeval dat wij ook tien vingers hebben....
Dit getallenstelsel heet dan ook het TIENTALLIGE stelsel.

Neem bijvoorbeeld het getal 35623 (vijfendertigduizend zeshonderdendrieëntwintig)
De cijfers 35623 staan dus (van rechts naar links) voor 3 • 10⁰ + 2 • 10¹ + 6 • 10² + 5 • 10³ + 3 • 10⁴

30000 + 5000 + 600 + 20 + 3 = 35623

En als we nou twee vingers hadden?

Nou ja... dan hadden we waarschijnlijk ook maar twee cijfers gehad; laten we ze 0 en 1 noemen.
Maar dat betekent dat we elke keer als het aantal knikkers boven de 1 uitkomt, we weer een nieuwe vak in het zand moeten maken......
Een knikker in het tweede vak vanaf rechts (een rode) telt dan voor 2 (blauwen).
Een knikker in het derde vak vanaf rechts (een groene) telt voor twee van 2 (twee roden) , en dat is 4 (blauwen).
enzovoorts.

Kortom: de cijfers zijn alleen maar nullen en enen, en ze tellen vanaf rechts gekeken mee voor 1, 2, 4, 8, 16, 32, 64, ...

Het getal 10110 staat voor (vanaf rechts) 0 + 1 • 2 + 1 • 4 + 0 • 8 + 1 • 16 = 22

Dit getallenstelsel met alleen maar enen en nullen heet het tweetallige stelsel (ook wel het binaire stelsel)

Kennen we iemand met naar twee vingers?

JAZEKER!!!!
Ik denk dat je hem zeker elke dag tegenkomt. De meeste mensen brengen tegenwoordig zelfs uren per dag met hem door.

Het is je computer/mobieltje/tablet!!!!

Kijk, zo'n apparaat werkt op elektriciteit, en simpel gezegd gaat het er dan om of er ergens spanning op staat (1) of niet (0)
Er zijn, elektrisch gezien, twee toestanden (twee cijfers): WEL (1) of GEEN(0) spanning.

Zo'n apparaat werkt dus met enen en nullen. Dus het moet wel berekeningen maken met getallen die uit enen en nullen bestaan. Twee mogelijke cijfers ....twee vingers.....tweetallig stelsel....

alle apparaten werken binair!!

.1.

Zet de volgende binaire getallen om in een "gewoon" getal.

11011

1111

1010101

111011

0100101

100010101

277

Van tientallig naar binair

Nou, dat is gelukkig heel simpel.
• Vraag je bij een getal af: Wat is het grootste getal uit de serie 1, 2, 4, 8, 16, 32, .... dat er in past?
• Op die plek in de serie ...2⁷ 2⁶2⁵ 2⁴ 2³2² 2¹ 2⁰ zet je een 1
• Kijk wat er dan overblijft als je die macht van 2 van jouw getal aftrekt.
• Vraag je weer af: wat is het grootste getal uit de serie 1, 2, 4, 8, 16, 32, dat in het overgebleven getal past?
enz.
Op alle plekken waar geen 1 staat, staat dus automatisch een 0.

voorbeeld. Schrijf het getal 361 als een binair getal.
Het grootste getal in het rijtje 1-2-4-8-16-32-64-128-256-512-...dat in de 361 past is 256
361 - 256 = 105 dus daarna past 128 er niet in, maar 64 wel.
105 - 64 = 41 dus daarna past 32 er in
41 - 32 = 9 dus daarna past 16 er niet in, maar 8 wel
dan blijft nog 1 over, dus 4 en 2 passen niet, maar 1 wel.

512	256	128	64	32	16	8	4	2	1
-	1	0	1	1	0	1	0	0	1

conclusie: 361 is binair 101101001

Zet de volgende getallen om in binaire getallen.

100

1100100

111111

620

1001101100

346

101011010

111001

1245

10011011101

Mijn kleine neefje heeft een leuke goocheltruc. Ik moet een getal tussen 1 en 64 in gedachten nemen. Daarna laat hij mij zes kaarten zien waarbij ik elke keer moet zeggen of mijn getal op die kaart staat of niet.

Na afloop weet hij precies mijn getal te noemen!!!

De kaarten die hij heeft staan hiernaast.

Eerst snap ik er helemaal niets van, totdat ik wat beter kijk naar de getallen linksboven in de kaarten.

Leg uit hoe de truc van mijn neefje werkt.

Optellen met binaire getallen.

Om op te tellen met binaire getallen kunnen we eerst het best kijken hoe dat gaat met "gewone" getallen.
Als je twee grote getallen moet optellen schrijf je ze meestal onder elkaar en telt de aparte cijfers op.

Dat ziet er dan ongeveer uit zoals hiernaast.
Je begint rechts en doet eerst 8 + 6
Dat is 14, en dan schrijf je 4 op en moet je "1 onthouden". Dat is die rode 1 daar boven.
Ik hoop dat je ziet dat dat eigenlijk niets anders is dan dat van de 14 blauwe knikkers in het vak van de enen er 10 worden doorgeschoven naar het vak ernaast; dat geeft 1 rode knikker in het vak van de tientallen.

Daarna doe je het volgende vak: 1 + 1 + 4 = 6
Dan komt 5 + 7 = 12 en daarvan noteer je weer de 2 en schuif je de andere 10 door naar het volgende vak: dat wordt weer een 1.

En nu binair. Dat gaat precies hetzelfde!
Alleen is een vak nu al te vol bij 2 knikkers

Bekijk de optelling hiernaast.
De meest rechtse kolom geeft 1 + 1 = 2
Maar die 2 past al niet, en moet al naar het volgende vak!
Dus 1 + 1 = 0 en eentje doorschuiven!
De tweede kolom (van rechts) geeft 1 + 0 + 0 = 1
De derde kolom geeft 1 + 1 = 0 en eentje doorschuiven

De vierde kolom geeft dan 1 + 1 + 1 = 3 dat betekent een 1 noteren in dit vak en die andere 2 als een 1 naar het volgende vak doorschuiven.

Op de site http://woodgears.ca/marbleadd/ zie je een prachtige toepassing van een binaire rekenmachine die op dit principe is gebouwd en werkt met........... knikkers!

Tel de volgende binaire getallen op:

110101 + 10110

1001011

1011 + 1101

11000

11111 + 10110

110101

101011 + 110010

1011101

Als je de drie getallen 1110 en 10111 en 11111 wilt optellen kun je natuurlijk eerst de eerste twee optellen en daarna die derde daar weer bij optellen.
Kun je het ook in één keer door ze alle drie onder elkaar te schrijven?