|
© h.hofstede (h.hofstede@hogeland.nl) |
||||
| OK, je hebt erom gevraagd..... | ||||
| We waren gebleven bij y' = c√(1 + y2) | ||||
|
|
||||
| De rechterkant primitiveren cx
+ d (met d één of andere constante) Blijft over het probleem om de linkerkant te primitiveren....... |
||||
| Als je zo'n vorm van 1 + y2
ziet staan is het vaak handig om de substitutie y = tanp
te gebruiken. Immers de afgeleide van tanp is tan2p + 1 en dat is dan dus y2 + 1. Voer de substitutie daarom maar uit: y = tanp en dy = (y2 + 1)dp geeft het volgende: (ik laat in de tussenstap y nog even staan) |
||||
|
|
||||
| Die laatste kunnen we handig veranderen: | ||||
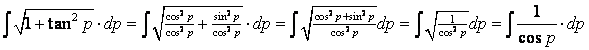 |
||||
| Nog maar even doorveranderen, het is zulk leuk werk... | ||||
|
|
||||
| Nu is die cosp daar in de
teller net de afgeleide van sinp in de noemer. Daarom gaan we
substitueren u = sinp Dan is namelijk du = cospdp en dat is precies wat er in de teller staat. |
||||
|
|
||||
| Bij de derde stap is de techniek
van "breuksplitsen" gebruikt. Hoe dat werkt staat in
deze les. Het geeft ook de extra factor 1/2 (reken dat zelf maar na). Nou, dan is het eindelijk zover: daar helemaal rechts staan nu twee integralen die we kunnen oplossen. De primitieve van 1/x is immers lnx. Denk nog wel even om de kettingregel bij de eerste; dat geeft een extra minteken. |
||||
|
|
||||
| Bij de laatste stap is uiteraard
gebruikt dat 1/2lnx
= ln√x, maar dat zag
je hopelijk al wel. Zo. Tijd om van u af te stappen en terug te gaan naar p: |
||||
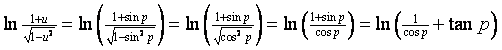 |
||||
| En daarna weer van p naar y. Daarvoor moet je eerst weer van die 1/cosp ook een tanp maken. Dat gaat zo: | ||||
|
|
||||
| En daarmee is dan eindelijk die integraal van helemaal aan het begin van deze les gevonden: | ||||
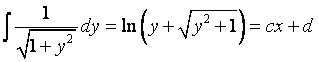 |
||||
| Eerst even iets over die
constante d. Ik hoop dat je je nog herinnert dat onze y de
helling van de kettingkromme was. Als we ervoor kiezen een ketting op te hangen met symmetrieas de y-as dan ligt het minimum bij x = 0. Dus moet de helling bij x = 0 gelijk zijn aan 0. Ofwel: als x = 0 moet ook y = 0 Invullen in bovenstaande vergelijking geeft dat d = 0 gekozen moet worden. Tot slot er nog even y = ... van maken. Dat kan met een leuke eigenschap van y + √(y2 + 1): |
||||
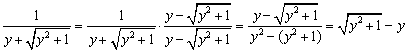 |
||||
| ln(y +
√(y2 +
1)) = cx geeft dan y +
√(y2 +
1) = ecx maar dan is √(y2 + 1) - y = e-cx (met die leuke eigenschap van net) Als je die twee van elkaar aftrekt dan hou je 2y over: 2y = ecx - e-cx Hè Hè, we zijn er: |
||||
|
||||
| Heb jij er ook zo'n voldaan gevoel over? | ||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
||||