© h.hofstede (h.hofstede@hogeland.nl)

Betrouwbaarheidsintervallen.
 - met de standaardnormale verdeling-
       
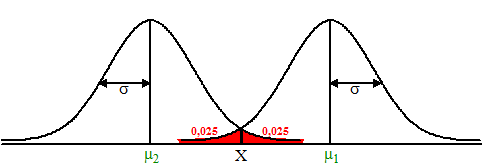
Eerst maar even de vorige les  samenvatten:

Stel dat we in een steekproef een meting van een gemiddelde X hebben gemeten, met een standaarddeviatie van σ.  Wat kunnen we dan bij een onbetrouwbaarheid van α zeggen over het werkelijke gemiddelde μ van de populatie?
Daar hoorden deze twee grensgevallen bij  (als voorbeeld bij  α = 0,05):
       

       
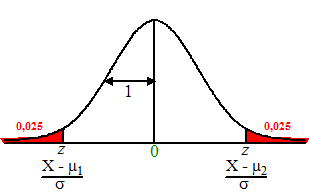
Met 95% zekerheid mochten we stellen dat het werkelijke gemiddelde tussen μ1 en μ2 zal zitten. Dat heette het betrouwbaarheidsinterval  [μ2, μ1].

Laten we overstappen op de standaardnormale verdeling.
Dan verandert  X in   z = (X - μ)/σ  De beide klokvormen in de figuur hierboven worden eigenlijk "in elkaar gedrukt" tot ze beiden de gewenste breedte σ = 1 hebben en daarna verschoven zodat μ1 en μ2 bij 0 komen te liggen. Zó dus:
       

       
Bedenk goed dat in deze figuur eigenlijk beide klokvormen hierboven over elkaar heen zijn geschoven zodat hun middens bij 0 komen te liggen.  De meetwaarde X komt dan bij beide z-waarden in de figuur terecht.

Maar voor die standaardnormale verdeling kunnen we gewoon de afstand van z tot het midden berekenen. Die is  1,96.

Als we dus een meting X hebben gedaan, dan vinden we de grenzen van het betrouwbaarheidsinterval doordat we weten dat X bij μ1 hoort bij  z = -1,96 en bij μ2 hoort bij  z = 1,96.
(X - μ1)/σ = -1,96  geeft   X - μ1 = -1,96σ  dus  μ1 = X + 1,96σ
(X - μ2)/σ = +1,96  geeft   X - μ2 = 1,96σ  dus  μ2 = X - 1,96σ
Dat geeft het betrouwbaarheidsinterval   [X - 1,96σ,   X + 1,96σ] 

En voor een andere a is die 1,96 ook een andere waarde natuurlijk.  Hier heb je een paar veel voorkomende waarden:
       
a z-waarde betrouwbaarheidsinterval
0,05 1,96 [X - 1,96σ,   X + 1,96σ] 
0,10 1,60 [X - 1,60σ,   X + 1,60σ] 
0,01 2,58 [X - 2,58σ,   X + 2,58σ] 
       
Bedenk daarbij wel dat die standaarddeviatie af kan hangen van de grootte van jouw steekproef. Als je bijvoorbeeld een populatie hebt waarin de standaarddeviatie gelijk is aan 2,8 en je doet een steekproef van 50, dan is voor het gemiddelde van die steekproef de standaarddeviatie gelijk aan  2,8/√50 = 0,396.
Dus als je een gemiddelde van een aantal metingen hebt genomen zul je die σ in de tabel steeds moeten vervangen door  σ/√n.

N.B.
Die 2,8 weet je natuurlijk nooit, want je kent de hele populatie niet.  Voorlopig nemen we even aan dat de standaarddeviatie van de hele populatie gelijk is aan de standaarddeviatie van je steekproef. In de volgende les zullen we daar dieper op in gaan.

Voorbeeld.
Een onderzoeker meet de lengte van een steekproef van 40 eerstejaarsstudenten, en vindt in zijn steekproef een gemiddelde van 172 cm met een standaarddeviatie van  29 cm.
Geef een 95%-betrouwbaarheidsinterval voor de hele populatie.

oplossing;
95% hoort bij  [X - 1,96σ,   X + 1,96σ]  en  σ = 29/√40 = 4,585
Dat geeft interval  [75 - 1,96 • 4,585,  75 + 1,96 • 4,585] = [163, 181]
       
OPGAVEN
       
1. De reactietijd van 80 willekeurig gekozen automobilisten in een steekproef  is gemiddeld 0,81 sec. met een standaarddeviatie van 0,20 sec.
Geef een 90%-betrouwbaarheidsinterval voor de gemiddelde reactietijd van de hele populatie.
     

[0.78, 0.85]
2. De hele bovenbouw van een grote scholengemeenschap heeft een rekentoets afgelegd. Een kleine steekproef onder 30 willekeurig gekozen leerlingen levert de volgende scores op:
       
 

34   56   78   65   76   70   54   64   60   96
50   67   80   53   67   68   76   52   52   88
44   45   59   90   62   73   61   60   55   57
       
  Geef een 95%-betrouwbaarheidsinterval voor de gemiddelde score van de hele scholengemeenschap.
     

 [58.7, 68.7]
       
     

© h.hofstede (h.hofstede@hogeland.nl)