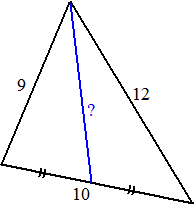© h.hofstede (h.hofstede@hogeland.nl)

De stellingen van Appollonius en Stewart.
       
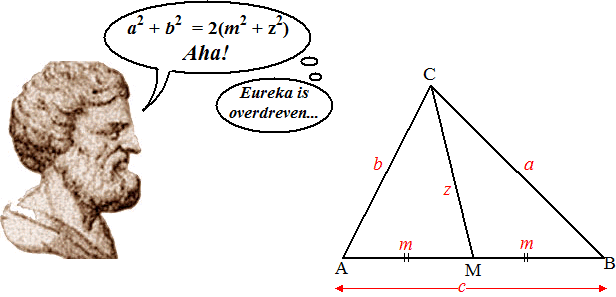
Van een driehoek ABC  is punt M het midden van AB.  De zwaartelijn CM heeft lengte z, en  AM = MB = m
Dan zegt de stelling van Appollonius:
 

       
Het bewijs is vrij eenvoudig:
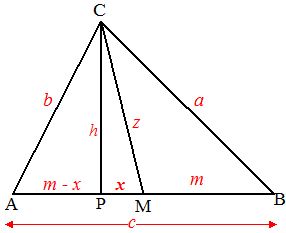
  Teken de hoogtelijn CP zoals hiernaast, en noem MP = x.

En nu gewoon drie keer Pythagoras:
in APC:   (m - x)2 + h2 = b2
in BPC:   (m + x)2 + h2 = a2
in PMC:  x2 + h2 = z2

a2 + b2 = (m - x)2 + h2 + (m + x)2 + h2     (de eerste en de tweede)
= m2 - 2mx + x2 + h2 + m2 + 2mx + x2 +  h2
= 2m2 + 2x2 + 2h2
= 2(m2 + x2 + h2)
= 2(m2 + z2)      (de derde)
■      
       
Appollonius voor gevorderden:  Stewart!
     
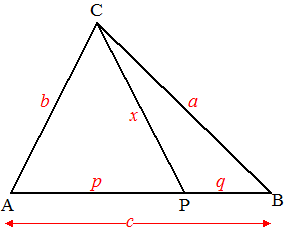
Wat gebeurt er als die M nou niet per se het midden van  AB is, maar een willekeurig punt P dat AB verdeelt in twee stukken AP = p  en  BP = q ?
(omdat CP geen zwaartelijn meer is noemen we die maar even  x)

Een algemener geval van de stelling van Appollonius dus.

Dan geldt de stelling van Stewart:
     

x2c  =  p •  a2 + q • b2 -  cpq 

     
(merk nog even op:  als p = q = m, en dus  c = 2m, en x = z   dan staat er 
2mz2 = ma2 + mb2 - 2m3  en als je alles door m deelt dan verschijnt daar Appollonius weer)
       
Het bewijs is ook goed te doen, als je de cosinusregel maar kent:
  in driehoek APC:  x2 = b2 + p2 - 2bp • cos(PAC)
in driehoek ABC:  a2 = b2 + c2 - 2bc • cos(BAC)
Die cosinus in beiden is dezelfde dus die gaan we weghalen.

Vermenigvuldig de eerste met  c  en de tweede met p:
x2c = b2c + p2c - 2bpc cos(hoek)
a2p = b2p + c2p - 2bpc cos(hoek)

Trek ze van elkaar af:

x2c - a2p = b2c - b2p + p2c - c2p
x2c - a2p = b2(c - p) + pc(p - c)     (die c - p is gelijk aan q, dus laten we die p - c ook omdraaien)
x2c - a2p = b2(c - p) - pc(c - p)
x2 - a2p = b2q - pcq
En nu gewoon nog even die a2p naar de andere kant en  Voilà:   je hebt de stelling van Stewart.
■      
       
Oké..... En kún je er ook nog iets mee?
       
1. de lengte van een zwaartelijn.
  Als P het midden van  AB is (Hallo Appollonius!!)  dan geeft deze stelling:
z2c  =  ½ca2  + ½cb2  -  ¼c3
z2 =   ½a2  + ½b2  -  ¼c2
Wacht, da's toch wel verdomd makkelijk! Laten we er daarom maar een kadertje omheen zetten:
       
 

zc2 =   ½a2  + ½b2  -  ¼c2

     

  Zo zie je direct dat de zwaartelijn hiernaast lengte z heeft waarvoor geldt:

z2 = ½ • 92 + ½ • 122  - ¼ • 102  = 62½

Dus z  = √62½ = 7,9056.....

Geef maar toe.....  Dat zou jij zomaar niet zo snel kunnen!
       
2. de lengte van een bissectrice.
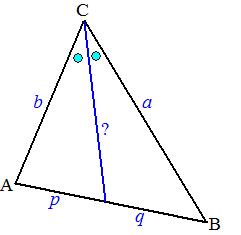
  Als je de bissectrice tekent, dan zijn die hoeken daar bovenin gelijk.
Maar wacht even...  de bissectricestelling zegt dat  p : q =  b : a
Dus is  ap = bq    .......(1)

(meer daarover kun je in deze les  over de stelling van Ceva lezen bij onderdeel 2).

Noem het vraagteken x, dan levert Stewart:
x2(p + q) =  pa2  + qb2 - (p + q) • pq     gebruik nu (1): 
x2(p + q) =  bqa  + apb - (p + q) • pq 
x2(p + q) =  ba(q + p) - (p + q) • pq   (delen door p + q) 
x2 = ba - pq
Vooruit, een kadertje maar weer:

     
 

xc2 = ba - pq
       

© h.hofstede (h.hofstede@hogeland.nl)