Vreemdere Sinusvormen.

© h.hofstede (h.hofstede@hogeland.nl)
       
Zo, je kent nu intussen de basis-sinusvorm  y = a + bsinc(x + d)
Daarin was a de evenwichtslijn, b de amplitude, en 2π/c de periode.,
Tijd om wat leven in de brouwerij te brengen.....

Die amplitude en die evenwichtslijn waren tot nu toe nogal saai. Laten we wat leukere vormen gaan bekijken.
       
1.  Andere evenwichtslijn.
       
Tot nu toe was de evenwichtslijn de horizontale lijn y = a.
Maar die evenwichtslijn kan natuurlijk best een andere soort grafiek zijn. Een grafiek kan natuurlijk net zo goed "heen en weer slingeren" rondom een stijgende lijn of een kromme lijn. Waarom zou dat horizontaal moeten zijn?
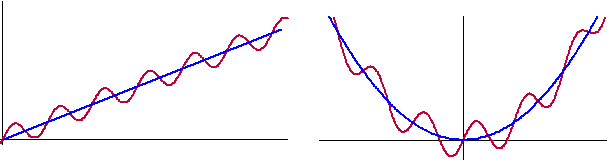
Hier zie je twee voorbeelden:
       

       
De blauwe lijn is de evenwichtslijn. Links een stijgende lijn, rechts een parabool. Zo'n evenwichtslijn die niet horizontaal is heet een trendlijn.
Het functievoorschrift van zo'n grafiek is eenvoudig: vervang gewoon de a uit de basisformule door een andere functie.
De linkergrafiek hierboven zou bijvoorbeeld de grafiek van  y = x + sinx kunnen zijn, en de rechter de grafiek van y = x2 + sinx.
In het algemeen zal het functievoorschrift zijn  y = f(x) + bsinc(x + d).
       
2.  Andere amplitude
       
De amplitude hoeft natuurlijk ook niet altijd zo'n saai constant getal b te zijn. Waarom zou die niet ook kunnen variëren?
Dat zal in praktijk ook vaak gebeuren:  denk bijvoorbeeld aan de uitwijking van een slinger. Door de luchtwrijving zal zo'n slinger langzaam steeds minder ver uitwijken en uiteindelijk stil gaan hangen.
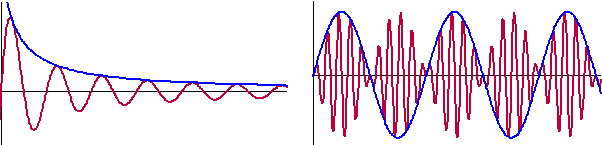
Hier zie je twee voorbeelden van een veranderende amplitude:
       

       
Ook deze functievoorschriften zijn niet moeilijk:  vervang de b van de amplitude door een andere functie (de blauwe in de figuren hierboven).
In het algemeen zal het functievoorschrift zijn:    y = a + f(x) • sinc(x + d).
Het rechtervoorbeeld is de amplitude wéér een sinusgrafiek (met veel grotere periode). Zo'n grafiek heet een zweving en daar zullen we later meer over behandelen.
       
       
  OPGAVEN
       
1. Over een hellend wegdek laat men een boomstam met diameter 50 cm met constante snelheid naar beneden rollen.
     
  a. Hoeveel omwentelingen maakt de stam
tussen A en B?
   

≈ 65
  In de onderste figuur zie je de grafiek van de hoogte h van punt P op de buitenkant van de stam als functie van de tijd t in seconden. Op t = 0 is P  in het punt A.
     
  b. Geef een functievoorschrift voor h(t).
     
         
2. Een bioloog onderzoekt met hydrocultuur welke factoren invloed hebben op de bladgroei van een bonenplant. Daartoe zet hij deze plant in een voedingsoplossing en houdt gedurende vijf dagen het specifieke bladgewicht (SBG) bij.  Later doet hij dit nog eens maar nu voegt hij een hoeveelheid NaCl toe aan de voedingsoplossing. De resultaten van beide proeven vind je in de figuur hiernaast. Daarin is t de tijd in dagen met t = 0 om 6 uur 's morgens.
Bij de tweede proef blijkt het SBG gemiddeld te stijgen

     
  a. Benader het SBG in de situatie zonder NaCl door een formule als functie van de tijd t in dagen.
     
  b. Doe het zelfde voor de situatie met NaCl
         
3. Een geit zit vast aan een touw, dat is vastgemaakt aan een paal met doorsnede 20 cm. De geit houdt het touw steeds strak, maar gaat rondjes lopen om de paal. In het begin staat de geit dus 10,1 meter rechts van het midden van de paal.
Het touw is 10 meter, maar wordt door dat rondlopen steeds korter, immers het windt zich rond de paal.
Neem aan dat de geit steeds dezelfde hoeksnelheid houdt (dat betekent dat hij over elk rondje evenveel tijd doet). Neem aan dat de geit over elk rondje 12 seconden doet.

Geef een vergelijking voor de afstand A links of rechts van het midden van de paal als functie van de tijd en schets de grafiek daarvan.
         

© h.hofstede (h.hofstede@hogeland.nl)