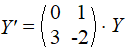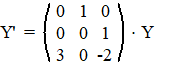© h.hofstede (h.hofstede@hogeland.nl)

       
Hogere orde differentiaalvergelijking:  Toch een Stelsel!
       
Nou we weten hoe we een stelsel differentiaalvergelijkingen aan moeten pakken kunnen we die wetenschap ook gaan gebruiken om één hogere orde differentiaalvergelijking op te lossen. Die is namelijk te herleiden tot een stelsel.
Dat doe je door y gewoon y1 te noemen en y' noem je y2 en y''  noem je y3  enzovoort. Alleen de hoogste afgeleide geef je geen andere naam.
Kijk hoe het werkt: in deze voorbeelden:

Voorbeeld 1:   Los op:    y'' + 2y' - 3y = 0      (met  y(0) = -1  en   y'(0) = 11)

Noem  y = y1 en y' = y2 .   Differentieer deze beide functies, en daar is het stelsel al:
y1'  = y'  = y2
y2'  = y '' = 4y - 2y'  = 4y1 - 2y2    ofwel:   

       
En dan gaan we onze kennis van de vorige les natuurlijk gebruiken:
Een algemene oplossing is dan : 

y1(0) = -1 geeft  c1 + c2 = -1
y2(0) = 11 geeft  c1 - 3c2 =  11
Dat geeft  c1 = 2 en c2 = -3
De oplossing van de oorspronkelijke vergelijking is alleen  y1, dus:    y(x) = 2ex - 3e-3x 

Voorbeeld 2:   Schrijf   y''' + 2y'' - 3y  = 0  als een stelsel.

Noem y = y1  en  y' = y2  en  y'' = y3   en ga deze functies differentiëren:
y1' = y' = y2
y2' = y'' = y3
y3' = y''' = -2y'' + 3y - 5  = -2y3 + 3y1  en dat geeft het stelsel:
       

       
       

© h.hofstede (h.hofstede@hogeland.nl)